Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод моделирования и использование мультимедийных средств в решении текстовых задач в 5 классе
Содержание
- 1. Метод моделирования и использование мультимедийных средств в решении текстовых задач в 5 классе
- 2. Объектом исследования является процесс
- 3. Цель
- 4. Глава 1. «Теоретические основы
- 5. Задачи на движение Мультимедийные презентации для уроков математики.
- 6. Встречное движение.Заглянем в конструктор
- 7. Движение в противоположных направлениях.Результат.
- 8. Движение с отставанием.Результат.
- 9. Движение вдогонку.Результат.
- 10. От Орла до Курска по шоссе 180
- 11. Опытно - экспериментальной базой исследования
- 12. Задачи практической работы:- подобрать
- 13. Слайд 13
- 14. 2. Формирующий экспериментЦель данного эксперимента: систематическое использование
- 15. - Давайте каждую величину поставим над ее
- 16. Задача 2: (№1106) «Два автобуса вышли в разное
- 17. Задача 7: (№ 1425)«Два теплохода движутся навстречу
- 18. Результат.№1359 Из города выехал велосипедист
- 19. Слайд 19
- 20. Слайд 20
- 21. Тема:«Сложение и вычитание десятичных дробей».
- 22. Цели урока:- закрепить навык сложения и вычитания
- 23. Слайд 23
- 24. Восстановите цепочки вычислений. 30:3:15+15+1960:20:9+14100:2080+19+20+30–90–50max 16
- 25. Слайд 25
- 26. Решите задачи:А) Собственная скорость теплохода 30,5км\ч. Скорость
- 27. Самостоятельная работа№1193,1194№ 1192(и-м)№1206
- 28. Домашняя работа:№1236(Б,Г)№1233
- 29. 3. Контрольный эксперимент. Была проведена самостоятельная работа
- 30. Слайд 30
- 31. Благодаря методу моделирования и
- 32. Спасибо за внимание!
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 «Метод моделирования и использование мультимедийных средств в решении текстовых задач
в 5 классе»
Слайд 2 Объектом исследования является процесс обучения пятиклассников решению
текстовых задач на уроках математики. Предметом исследования
является пути повышения эффективности обучения решению задач посредством метода моделирования и мультимедийных средств в математике.Слайд 3 Цель исследования:
разработка различных вспомогательных моделей, слайдов,
презентаций используемых при обучении решению текстовых задач в 5 классе общеобразовательной школы.Достижение цели предполагает решение ряда задач:
1. Изучить научную, методическую литературу
об использовании метода моделирования и мультимедийных средств при решении текстовых задач.
2. Разработать вспомогательные модели для решения текстовых задач на уроках математики.
3. Экспериментально проверить эффективность разработанных уроков и проанализировать их.
Гипотеза: использование метода моделирования и мультимедийных средств способствует успешному формированию умения решать текстовые задачи.
Слайд 4Глава 1. «Теоретические основы использования
метода моделирования и мультимедийных средств в процессе
обучения математики»1. Понятие модели и моделирования процессе обучения.
Модель – искусственно созданный объект в виде схемы, чертежа, логико – математических знаковых формул, физической конструкции и т.п.
Моделирование – это деятельность по построению (конструированию) моделей для указанных целей.
2. Метод моделирования текстовых задач.
План решения задачи.
1. Анализ задачи.
2. Поиск плана решения задачи.
3. Осуществление плана решения задачи.
4. Проверка решения задачи.
В процессе решения задачи четко выделяются три этапа математического моделирования:
I этап – это перевод условий задачи на математический язык; при этом выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними;
II этап – внутримодельное решение (т.е. нахождение значения выражения, выполнение действий, решение уравнения);
III этап – интерпретация, т. е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача.
3.Использование мультимедийных средств в решении текстовых задач.
Слайд 6
Встречное движение.
Заглянем в конструктор слайдов. В списке
две анимации. Для группы 1 и группы 32. Время начала
– вместе с предыдущим.Результат.
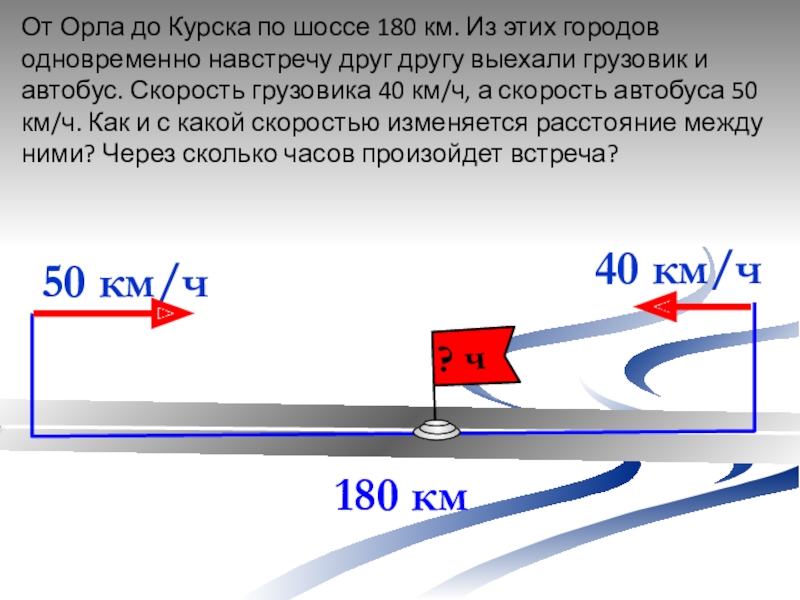
Слайд 10От Орла до Курска по шоссе 180 км. Из этих
городов одновременно навстречу друг другу выехали грузовик и автобус. Скорость
грузовика 40 км/ч, а скорость автобуса 50 км/ч. Как и с какой скоростью изменяется расстояние между ними? Через сколько часов произойдет встреча?180 км
Слайд 11 Опытно - экспериментальной базой исследования явилась МКОУ СОШ
№4.
В эксперименте участвовал 5 класс в количестве 14 учащихся.
Слайд 12 Задачи практической работы:
- подобрать задания для проверочной
работы;
- провести срезовую работу по решению задач;
- проанализировать допущенные ошибки;
-
апробировать систему задач с использованием моделей;- провести контрольную работу;
- сравнить количество допущенных ошибок;
- сделать выводы по использованию метода моделирования и использование мультимедийных средств при решении задач.
Слайд 13
Исследование проводилось в три этапа: 1) констатирующий эксперимент; 2)
формирующий эксперимент; 3) контрольный эксперимент.1. Констатирующий эксперимент.
Цель: выявить, насколько сформированы навыки решения задач у учащихся 5 класса
на исходном этапе эксперимента.
Для этого была предложена самостоятельная работа на решение задач по теме «Формулы». Каждый ученик должен был решить две задачи на движение.
Несмотря на то, что задачи были знакомы, многие не справились с их решением и допустили большое количество ошибок.
1. Количество учащихся по списку - 14
2. Выполняли работу - 14
3. Выполнили всю работу без ошибок - 6 (43 %)
4. Ошиблись в задаче № 1 - 2 (14 %)
5. Ошиблись в задаче № 2 - 3 (21,5 %)
6. Не справились с работой - 3 (21,5 %)
На исходном этапе эксперимента навыки решения задач у учащихся 5 классов находятся на среднем уровне развития.
Слайд 142. Формирующий эксперимент
Цель данного эксперимента: систематическое использование метода моделирования
и мультимедийных средств при
решении задач в 5 классе.Для этого классу предлагалось, почти каждый урок, решать задачи с использованием метода моделирования и мультимедийных средств.
Н-р: Задача №1
«Автомобиль «Жигули» за 3 часа может проехать 360 км. Бескрылая
птица страус – лучший бегун в мире – развивает скорость до 120 км/ч.
Сравните скорости автомобиля и страуса»
- Внимательно слушаем условие задачи.
1. Чтение задачи и запись условия.
- О чем это задача? (Об автомобиле «Жигули» и о страусе)
- Знаете автомобиль «Жигули»?
- Страус знаете?
- Что нам уже известно в задаче? (Автомобиль «Жигули» за 3 часа может проехать 360 км. Бескрылая птица страус развивает скорость до 120 км/ч)
- Давайте составим таблицу:
- Как найти скорость, время, расстояние.( S=v*t, S:t=v, S:v=t)
Слайд 15
- Давайте каждую величину поставим над ее обозначением.
- Что мы
должны узнать? (Сравнить скорости автомобиля и страуса)
- Можем сразу
сравнить? (Нет)- Почему? (Должны найти скорость автомобиля)
- Поставим над знаком скорости вопросительный знак.
2. Анализ задачи и составление плана решения.
- Посмотрите внимательно на таблицу.
- Какой главный вопрос задачи? (Сравнить скорости автомобиля и страуса?)
- Можно сразу ответить на этот вопрос? (Нет)
- Почему? (Должны найти скорость автомобиля)
- Как? (расстояние делим на время (S:t=v)по формуле S=v*t, 360:3=120)
- Теперь сможем сравнить? (Да)
- Что для этого нужно сделать? (Сравнить скорость автомобиля и страуса)
3. План решения.
Еще раз посмотрим, как мы решили эту задачу:
- нашли скорость автомобиля «Жигули»;
- и сравнили со скоростью страуса.
4. Осуществление плана решения.
- Предлагаю записать самостоятельно решение задачи по действиям с пояснениями.
1) 360:3=120 (км/ч) – скорость автомобиля «Жигули»
2) 120=120
Ответ: скорость автомобиля и страуса равны
Слайд 16
Задача 2: (№1106)
«Два автобуса вышли в разное время навстречу друг
другу из двух городов, расстояние между которыми 480 км. Скорость
первого автобуса 52км/ч, а скорость второго 42км/ч. Пройдя 312 км, первый автобус встретился со вторым. На сколько часов первый автобус вышел раньше второго?»
52 км/ч 42 км/ч
312 км
480 км
480-312=168 (км)- пройденный путь второго автобуса
2) 312:52=6 (ч)- прошел первый автобус, за 312км.
3) 168:42=4 (ч)- прошел второй автобус, за 168км.
4) 6-4=2 (ч)- раньше вышел первый автобус.
Ответ: 2ч.
Слайд 17
Задача 7: (№ 1425)
«Два теплохода движутся навстречу друг другу. Сейчас
между ними 185,5 км. Первый теплоход имеет собственную скорость 24,5
км/ч и движется по течению, а второй теплоход имеет собственную скорость 28,5 км/ч и движется против течения. Через сколько часов они встретятся, если скорость течения 2,5км/ч.»- Для решения данной задачи сделаем схему и таблицу.
24 км/ч 28 км/ч
t=?
2,5 км/ч
185,5 км
1) 24,5+ 2,5=27 (км/ч)- скорость первого теплохода по течению
2) 28,5-2,5=26 (км/ч)- скорость второго теплохода против течения
3) 27+26 =53 (км/ч) - скорость обоих теплоходов вместе взятых
4) 185,5 : 53= 3,5 (ч) - они встретятся
Ответ: 3,5 ч.
Слайд 18
Результат.
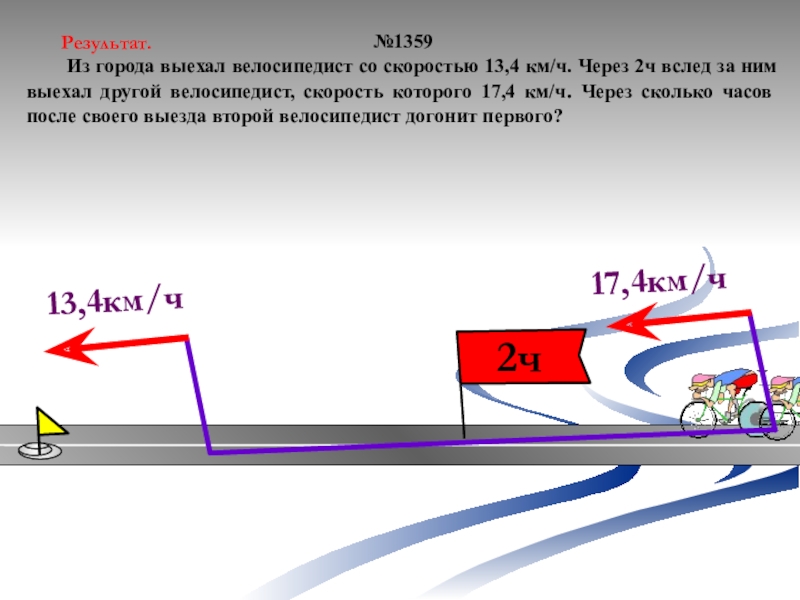
№1359
Из города выехал велосипедист со скоростью 13,4
км/ч. Через 2ч вслед за ним выехал другой велосипедист, скорость
которого 17,4 км/ч. Через сколько часов после своего выезда второй велосипедист догонит первого?17,4км/ч
13,4км/ч
2ч
Слайд 19
177,6 км
за 6ч.
2,8 км/ч
Найдите собственная скорость катера
Против течения
№1361Катер, двигаясь против течения, за 6 ч прошел 177,6 км. Найдите собственную скорость катера, если скорость течения равна 2,8 км/ч.
Слайд 20
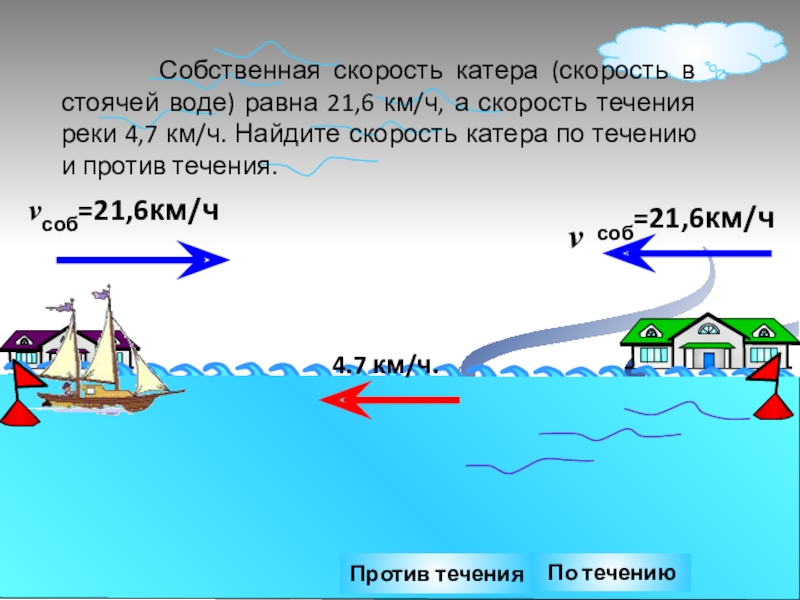
4.7 км/ч.
Против течения
По течению
Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения.
Слайд 22Цели урока:
- закрепить навык сложения и вычитания десятичных дробей при
решении задач «движение по реке»;
- развивать вычислительные навыки, внимание;
- воспитывать
усидчивость, терпение, самостоятельность.Оборудование: наглядность для устных упражнений, карточки с дополнительными заданиями.
Слайд 23
Ход урока
I. Организационная часть
II. Проверка домашнего задания
III.Устные упражнения.
1.Составьте
текст задачи, используя чертеж.Какие вопросы можно поставить к задаче, чтобы в решении было сложение и вычитание дробей
2,8км/ч 24,9 км/ч
плот катер
А В
Слайд 25
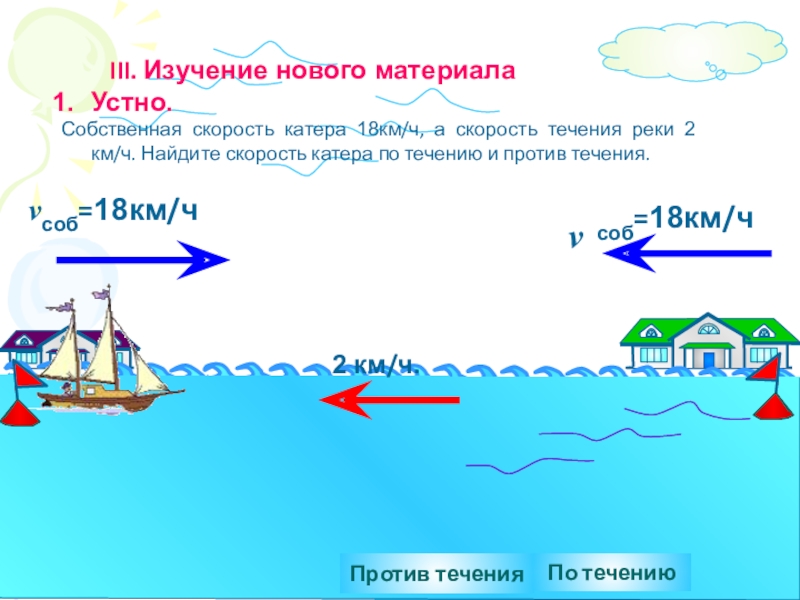
2 км/ч.
Против течения
По течению
III. Изучение нового материала
Устно.
Собственная скорость катера 18км/ч, а скорость течения реки 2 км/ч. Найдите скорость катера по течению и против течения.
Слайд 26Решите задачи:
А) Собственная скорость теплохода 30,5км\ч. Скорость течения 2,8км\ч.Найдите скорость
теплохода против течения и его скорость по течению.
Б) Собственная скорость
теплохода v км\ч. Скорость течения m км\ч. Заполните таблицу:Слайд 293. Контрольный эксперимент. Была проведена самостоятельная работа по теме «Решение
задач на движение».
Цель: выявление наличия или отсутствия умений решать
задачи, используя метод моделирования и использование мультимедийных средств.Получены следующие результаты:
1. Количество учащихся по списку - 14
2. Выполняли работу -14 (100 %)
3. Решили все задачи без ошибок 10 (71%)
4. Ошиблись в первой задаче 1 (7 %)
5. Ошиблись во второй задаче 1 (7 %)
6. Не справились с решением задач – 2 (15%)
Проанализировав данные результаты, можно сделать вывод, что класс выполнил работу намного лучше, чем в констатирующем этапе. Дети в большинстве своем использовали модели при решении задач.
Слайд 30
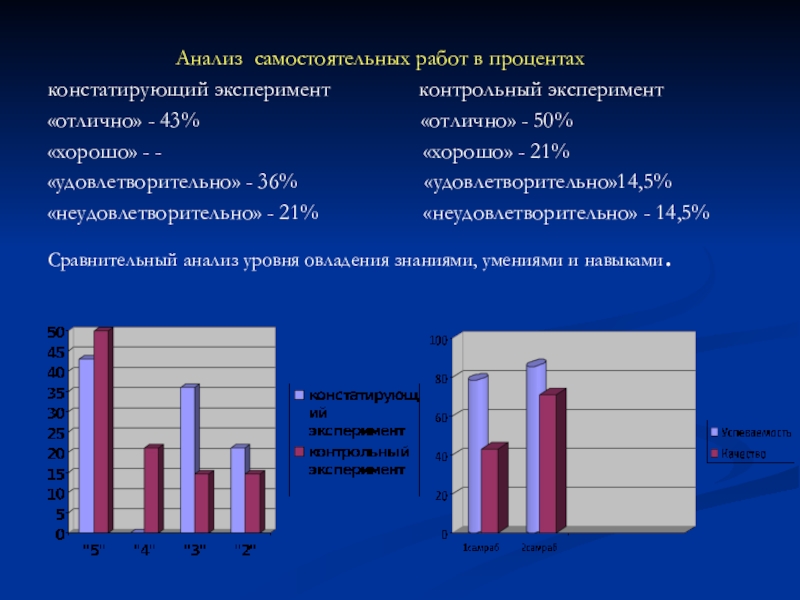
Анализ самостоятельных работ в процентах
констатирующий эксперимент
контрольный эксперимент«отлично» - 43% «отлично» - 50%
«хорошо» - - «хорошо» - 21%
«удовлетворительно» - 36% «удовлетворительно»14,5%
«неудовлетворительно» - 21% «неудовлетворительно» - 14,5%
Сравнительный анализ уровня овладения знаниями, умениями и навыками.