Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод параллельного проектирования
Содержание
- 1. Метод параллельного проектирования
- 2. Итак, мы приступили к изучению стереометрии –
- 3. АВыберем в пространстве произвольную плоскость α (её
- 4. АαаПроведем через точку А прямую, параллельную прямой
- 5. Рассматривая любую геометрическую фигуру как множество точек,
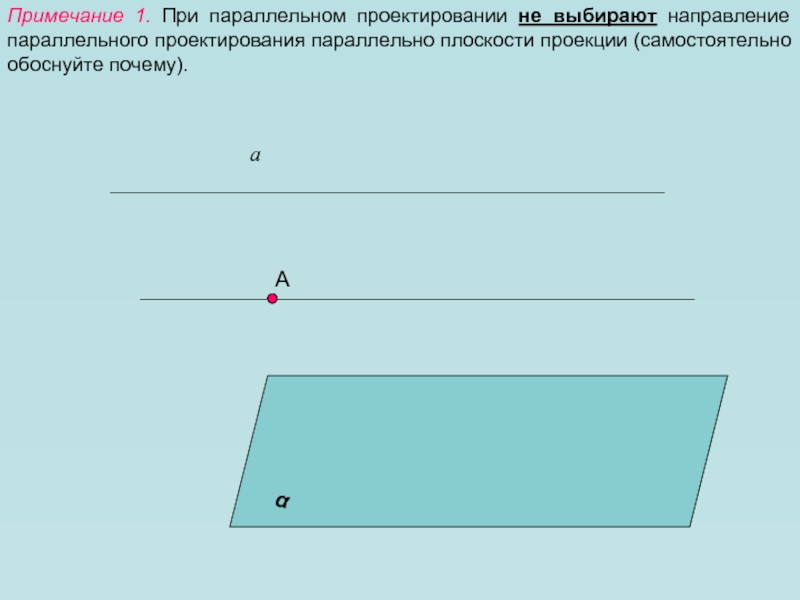
- 6. Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции (самостоятельно обоснуйте почему).Ааα
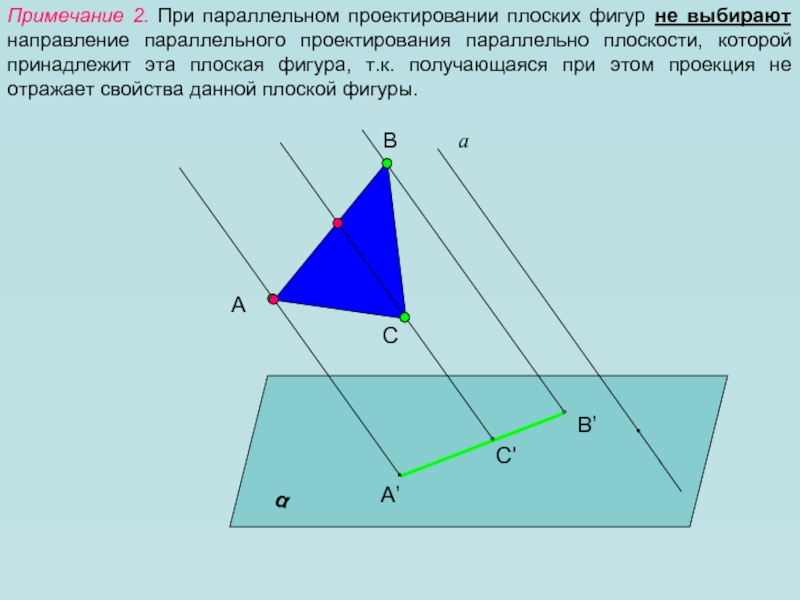
- 7. Примечание 2. При параллельном проектировании плоских фигур
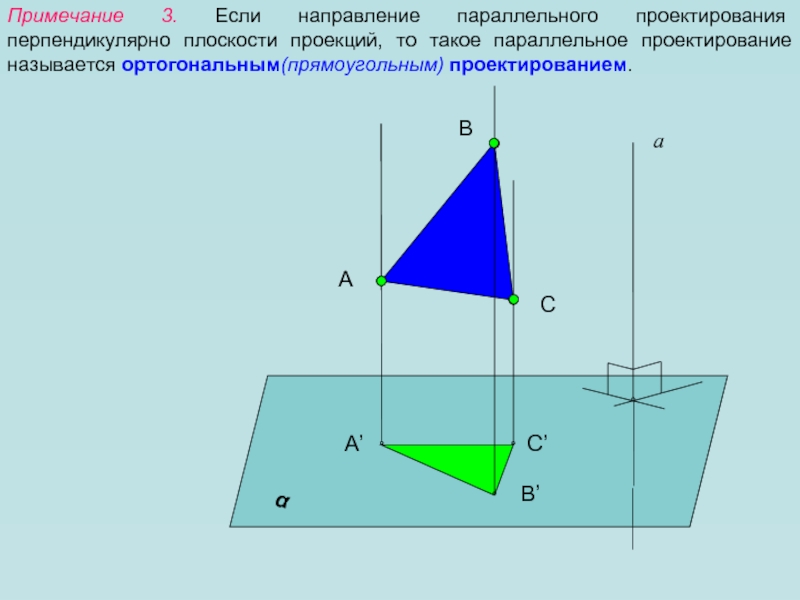
- 8. Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным(прямоугольным) проектированием.АаαBCА’B’C’
- 9. Примечание 4. Если плоскость проекций и плоскость,
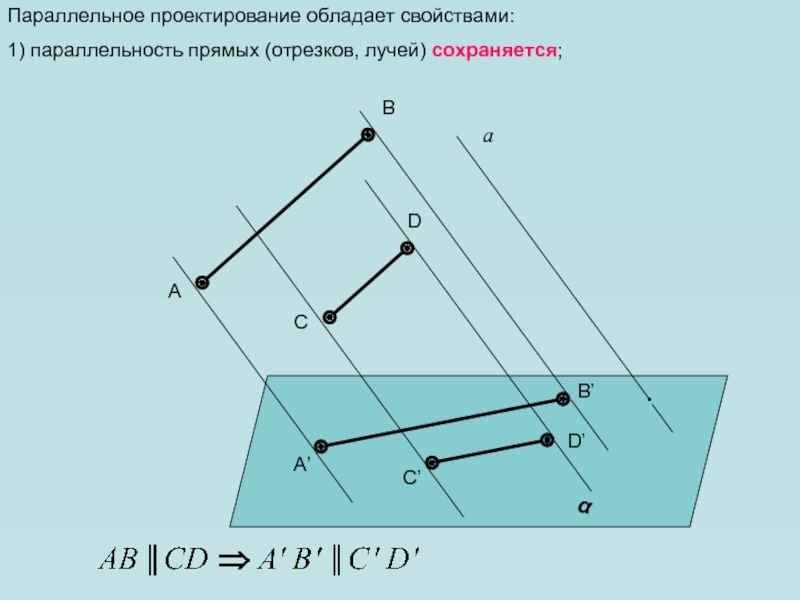
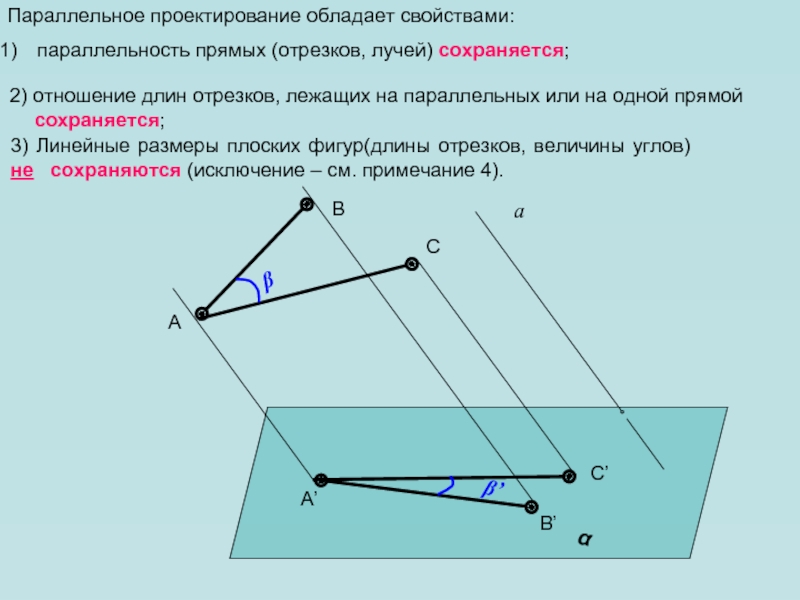
- 10. Параллельное проектирование обладает свойствами:1) параллельность прямых (отрезков, лучей) сохраняется;αаADCBA’D’C’B’
- 11. 2) отношение длин отрезков, лежащих на
- 12. Параллельное проектирование обладает свойствами:параллельность прямых (отрезков, лучей)
- 13. αИтак, построим изображение куба:Далее разберем примеры изображения некоторых плоских фигур…
- 14. Фигура в пространствеЕё изображение на плоскостиПроизвольный треугольникПроизвольный треугольникПрямоугольный треугольникПроизвольный треугольникРавнобедренный треугольникПроизвольный треугольник
- 15. Фигура в пространствеЕё изображение на плоскостиРавносторонний треугольникПроизвольный треугольникПараллелограммПроизвольный параллелограммПрямоугольникПроизвольный параллелограмм
- 16. Фигура в пространствеЕё изображение на плоскостиКвадратПроизвольный параллелограммТрапецияПроизвольная трапецияПроизвольный параллелограммРомб
- 17. Фигура в пространствеЕё изображение на плоскостиРавнобокая трапецияПроизвольная трапецияПрямоугольная трапецияПроизвольная трапецияКруг (окружность)Овал (эллипс)
- 18. ABCDEFOРазберемся, как построить изображение правильного шестиугольника.FABCDEРазобьем правильный
- 19. ABCDEПопробуйте самостоятельно построить изображение правильного пятиугольника.Подсказка: разбейте
- 20. Скачать презентанцию
Итак, мы приступили к изучению стереометрии – геометрии в пространстве. Как всегда нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске
Слайды и текст этой презентации
Слайд 1Метод параллельного проектирования. Изображение пространственных фигур на плоскости.
Геометрия,
10 класс.
Воробьев
Леонид Альбертович, г.Минск
Слайд 2Итак, мы приступили к изучению стереометрии – геометрии в пространстве.
Как всегда нам необходимо уметь изображать геометрические фигуры, причем все
чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске и т.д.). Каким образом пространственную фигуру (например, куб) можно «уложить» в плоскость?Для решения этой задачи применяется метод параллельного проектирования. Выясним его суть на примере простейшей геометрической фигуры – точки.
Итак, у нас есть геометрическая фигура в пространстве – точка А.
А
Слайд 3
А
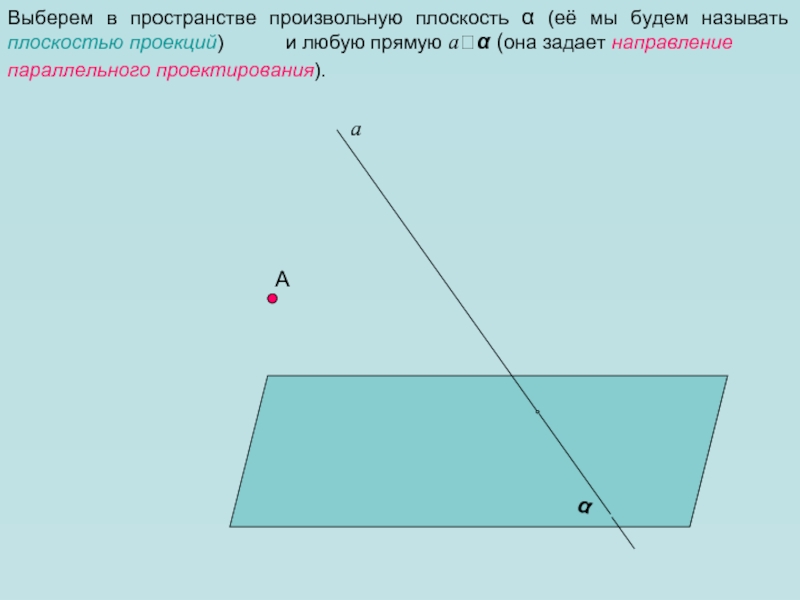
Выберем в пространстве произвольную плоскость α (её мы будем называть
плоскостью проекций)
α
и любую прямую aα (она задает направление
параллельного проектирования).
а
Слайд 4А
α
а
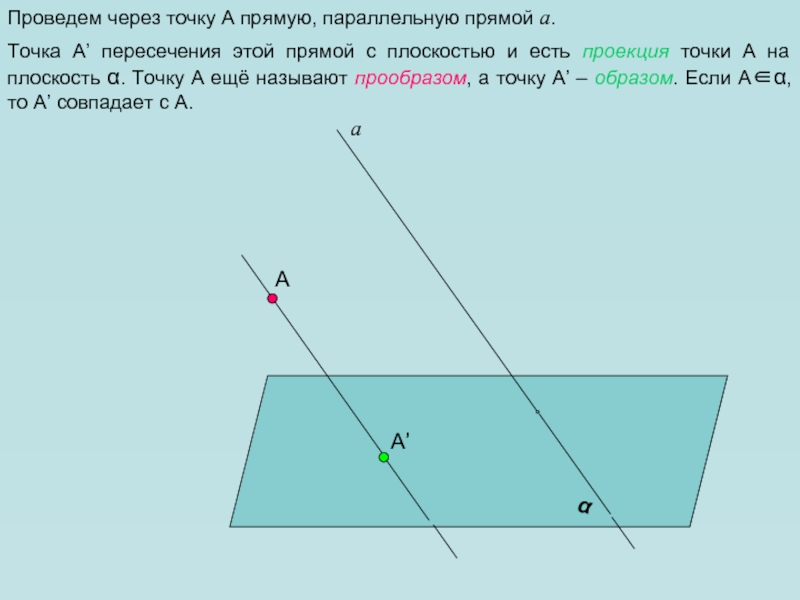
Проведем через точку А прямую, параллельную прямой а.
А’
Точка А’ пересечения
этой прямой с плоскостью и есть проекция точки А на
плоскость α. Точку А ещё называют прообразом, а точку А’ – образом. Если А∈α, то А’ совпадает с А.
Слайд 5
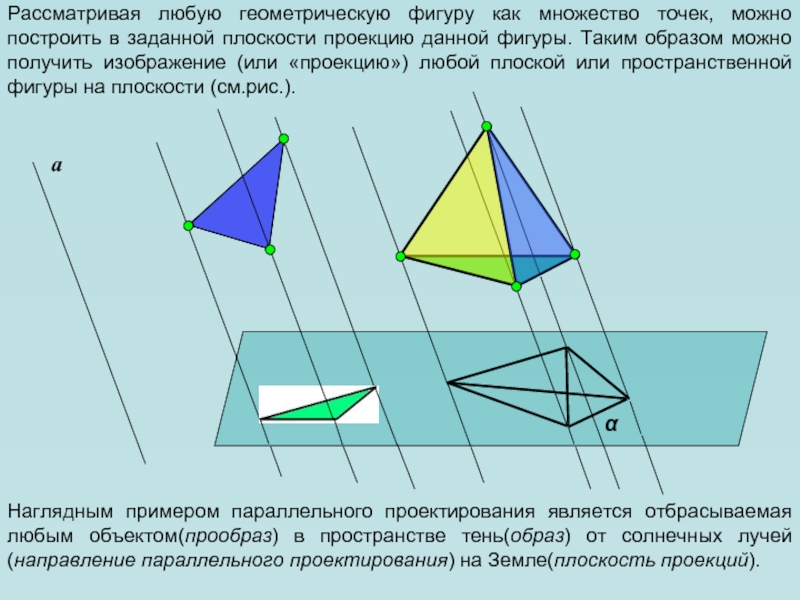
Рассматривая любую геометрическую фигуру как множество точек, можно построить в
заданной плоскости проекцию данной фигуры. Таким образом можно получить изображение
(или «проекцию») любой плоской или пространственной фигуры на плоскости (см.рис.).а
α
Наглядным примером параллельного проектирования является отбрасываемая любым объектом(прообраз) в пространстве тень(образ) от солнечных лучей(направление параллельного проектирования) на Земле(плоскость проекций).
Слайд 6Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования
параллельно плоскости проекции (самостоятельно обоснуйте почему).
А
а
α
Слайд 7
Примечание 2. При параллельном проектировании плоских фигур не выбирают направление
параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к.
получающаяся при этом проекция не отражает свойства данной плоской фигуры.А
а
α
B
C
А’
B’
C’
Слайд 8
Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то
такое параллельное проектирование называется ортогональным(прямоугольным) проектированием.
А
а
α
B
C
А’
B’
C’
Слайд 9
Примечание 4. Если плоскость проекций и плоскость, в которой лежит
данная фигура параллельны (α||(АВС)), то получающееся при этом изображение…
А
а
α
B
C
А’
B’
C’
…правильно
– равно прообразу! 
Слайд 10Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
α
а
A
D
C
B
A’
D’
C’
B’
Слайд 11 2) отношение длин отрезков, лежащих на параллельных или на
одной прямой сохраняется;
Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется;
α
а
A
D
C
B
A’
D’
C’
B’
Если,
например, АВ=2CD, то А’В’=2C’D’ илиМ
М’
Слайд 12Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется;
α
а
A
B
A’
B’
3) Линейные размеры
плоских фигур(длины отрезков, величины углов) не сохраняются (исключение –
см. примечание 4). 2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется;
β
β’
C
C’
Слайд 13
α
Итак, построим изображение куба:
Далее разберем примеры изображения некоторых плоских фигур…
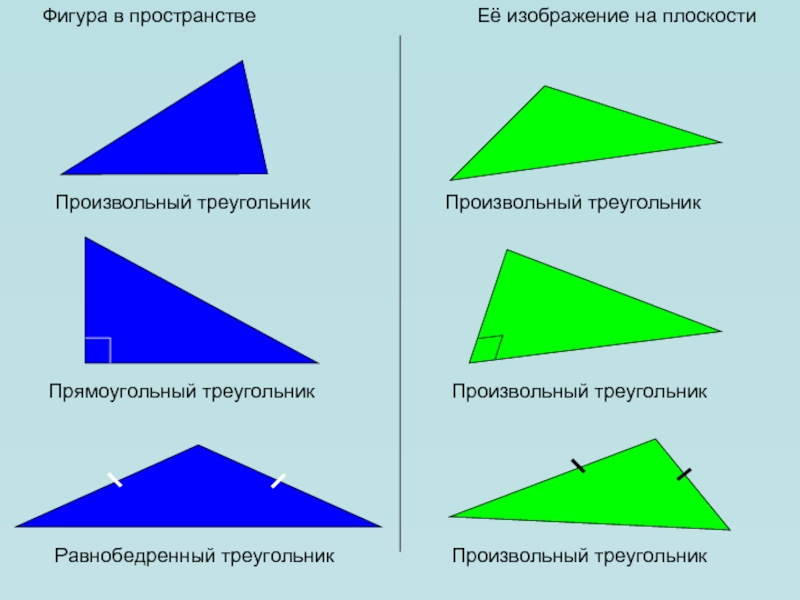
Слайд 14Фигура в пространстве
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Прямоугольный треугольник
Произвольный треугольник
Равнобедренный
треугольник
Произвольный треугольник
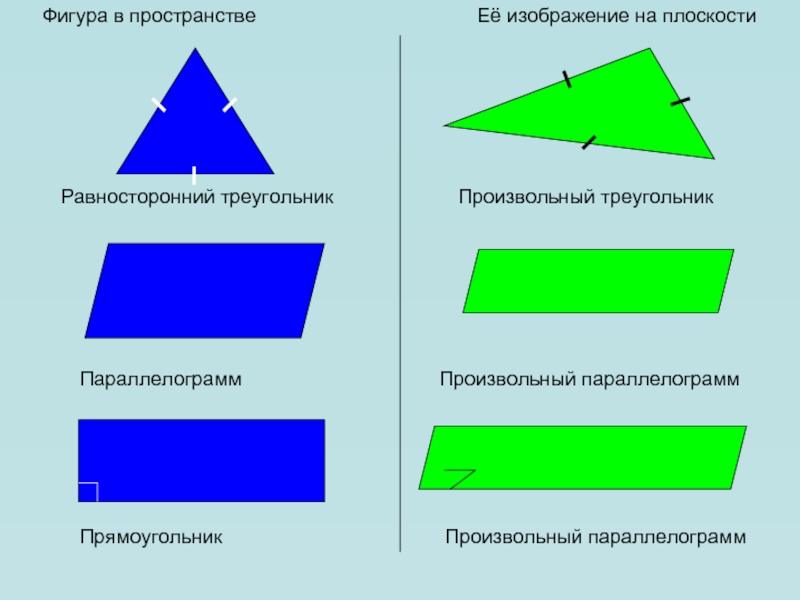
Слайд 15Фигура в пространстве
Её изображение на плоскости
Равносторонний треугольник
Произвольный треугольник
Параллелограмм
Произвольный параллелограмм
Прямоугольник
Произвольный параллелограмм
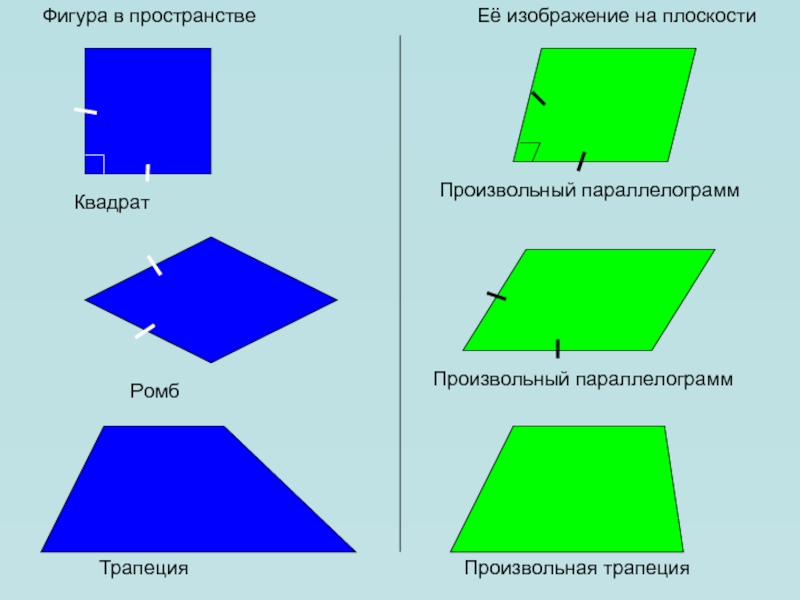
Слайд 16Фигура в пространстве
Её изображение на плоскости
Квадрат
Произвольный параллелограмм
Трапеция
Произвольная трапеция
Произвольный параллелограмм
Ромб
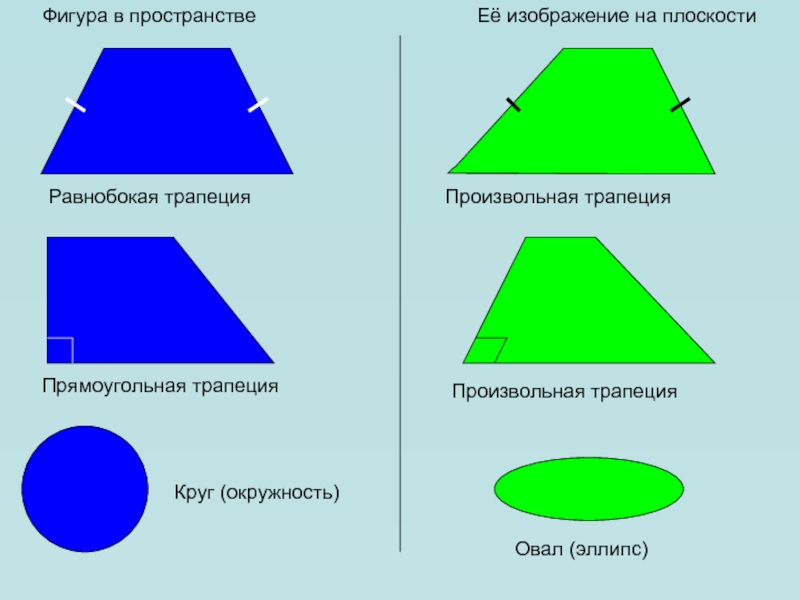
Слайд 17Фигура в пространстве
Её изображение на плоскости
Равнобокая трапеция
Произвольная трапеция
Прямоугольная трапеция
Произвольная трапеция
Круг
(окружность)
Овал (эллипс)
Слайд 18
A
B
C
D
E
F
O
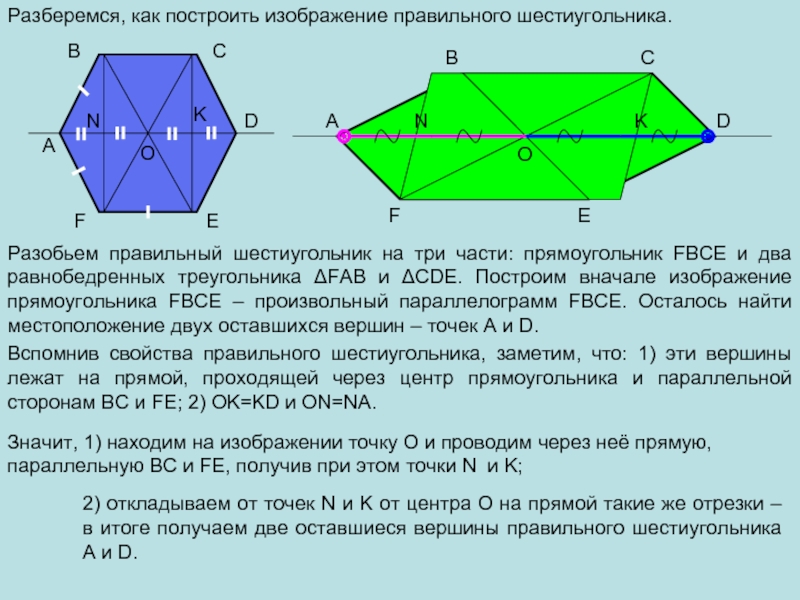
Разберемся, как построить изображение правильного шестиугольника.
F
A
B
C
D
E
Разобьем правильный шестиугольник на три
части: прямоугольник FBCE и два равнобедренных треугольника ΔFAB и ΔCDE.
Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE. Осталось найти местоположение двух оставшихся вершин – точек A и D.Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE; 2) OK=KD и ON=NA.
K
N
Значит, 1) находим на изображении точку О и проводим через неё прямую, параллельную BC и FE, получив при этом точки N и K;
O
N
K
2) откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D.
Слайд 19
A
B
C
D
E
Попробуйте самостоятельно построить изображение правильного пятиугольника.
Подсказка: разбейте фигуру на две
части – равнобокую трапецию и равнобедренный треугольник, а затем воспользуйтесь
некоторыми свойствами этих фигур и ,конечно же, свойствами параллельного проектирования.A
C
D
E
Решение. Просмотрите ход построения…
B
Теги
