Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Межпредметные связи на примере темы Степенная функция в рамках курса основной школы
Содержание
- 1. Межпредметные связи на примере темы Степенная функция в рамках курса основной школы
- 2. «Пусть кто-нибудь попробует вычеркнуть из математики степени,
- 3. Цели межпредметной учебной деятельности для учителя.
- 4. Результаты межпредметной учебной деятельности для учителя.
- 5. Результаты межпредметной учебной деятельности для учителя.
- 6. 5-6 класс
- 7. Эволюция понятия степени в курсе основной школы.
- 8. 7 класс
- 9. Слайд 9
- 10. Свойства степени с натуральным показателем1 свойство: aman
- 11. Пример решения задач в математике:
- 12. Пример решения задач в математике: Записать в виде степени с основанием а.
- 13. 1 кг = 1000 г, 1 м3 = 1000000 см3
- 14. Например, плотность льда равна 900 кг/м3 , а меди 8,9 г/см3. Значит,
- 15. Пример решения задачи: В первом примере учащиеся
- 16. 8 класс
- 17. Слайд 17
- 18. Свойства степеней 8 класса понятие отрицательной степени):
- 19. Упростите выражение:
- 20. Пример решения задач в математике:
- 21. Пример решения задачи: В данной задаче учащиеся при выполнении испытывают трудности при вынесении общего множителя.
- 22. Запись удельных единиц в 8 классеУдельная теплоёмкость
- 23. Пример решения задачи:
- 24. Пример решения задачи: В данной задаче учащиеся
- 25. Слайд 25
- 26. Пример решения задачи:
- 27. Пример решения задачи:
- 28. Слайд 28
- 29. Пример решения задач для подготовки к ОГЭ
- 30. Задача:В таблице приведены расстояния от Солнца до
- 31. Решение:
- 32. Площадь территории Казахстана составляет 2,7 млн км2.
- 33. Условие:В таблице приведены расстояния от Солнца до четырёх
- 34. Выводы:
- 35. Выводы:
- 36. Учащиеся умеют :Привлекать и привлекают понятия и
- 37. В завершении работы секции мы просим вас
- 38. Спасибо. 1 2 3 4 5
- 39. Скачать презентанцию
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов
Слайды и текст этой презентации
Слайд 1Мастер-класс
Межпредметные связи на примере темы «Степенная функция» в рамках курса
основной школы.
Слайд 2«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит,
что без них далеко не уедешь»
М.В. Ломоносов
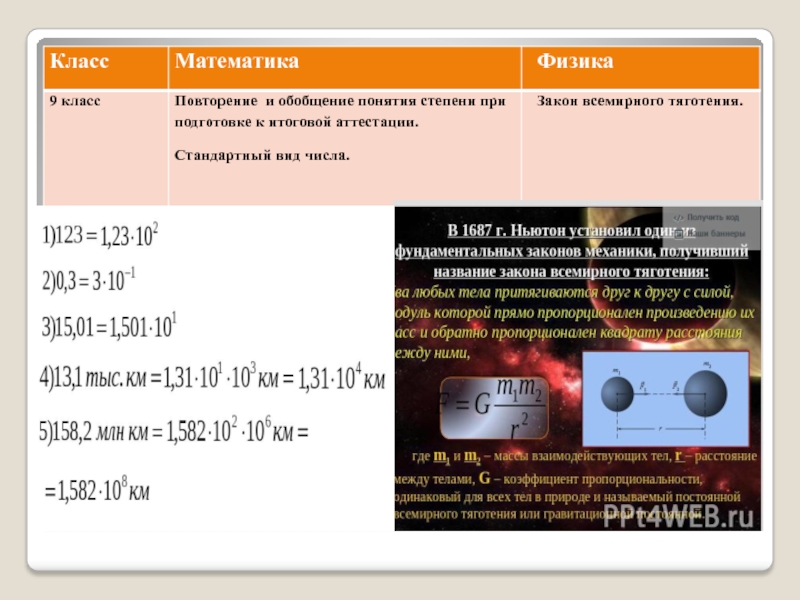
Слайд 10Свойства степени с натуральным показателем
1 свойство: aman = am+n
2 свойство:
am:an = am-n; (а 0; mn)
3 свойство: (am)n = amn
4
свойство: (ab)n = anbn
5 свойство:
; (b 0)
Слайд 15Пример решения задачи:
В первом примере учащиеся при выполнении не испытывают
никаких затруднений, а во втором сталкиваются с затруднениями при сокращении
и преобразованиями (сократить метры и кубические метры).
Слайд 21Пример решения задачи:
В данной задаче учащиеся при выполнении испытывают трудности
при вынесении общего множителя.
Слайд 22Запись удельных единиц в 8 классе
Удельная теплоёмкость воды равна 4200
Дж/кг С.
Удельная теплота плавления льда равна 3,4 .105
Дж/кг. Удельная теплота парообразования воды равна 2,3. 106 Дж/кг.
Удельная теплота сгорания спирта равна 2,7. 107 Дж/кг.
Слайд 24Пример решения задачи:
В данной задаче учащиеся при выполнении преобразований в
ответе количества теплоты записать ответ лучше с помощью стандартной записи
числа, которая в курсе алгебры изучается в 9 классе.
Слайд 29
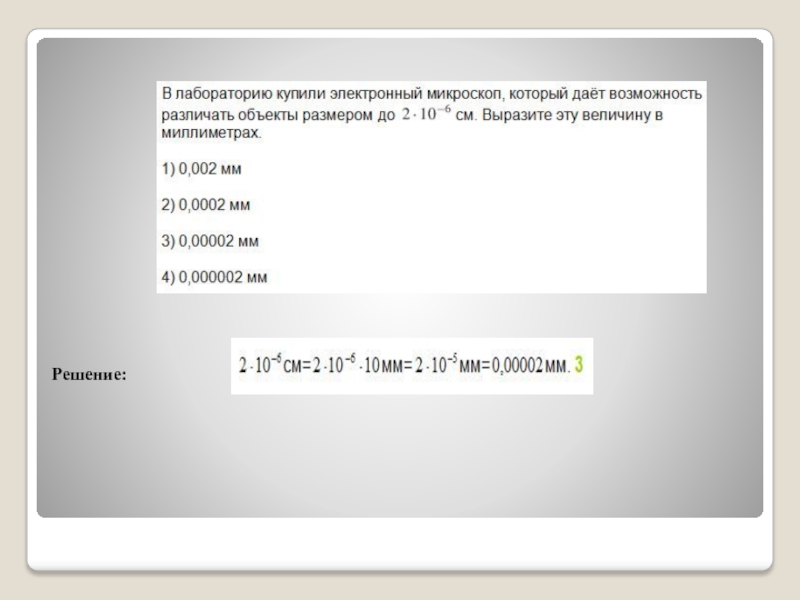
Пример решения задач для подготовки к ОГЭ и ЕГЭ, использующие
свойства степеней и преобразований со степенями:
Расстояние от наблюдателя, находящегося на
небольшой высоте h километров над землей до наблюдаемой им линии горизонта вычисляется по формуле:С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
Задача сводится к решению уравнения:
Горизонт на расстоянии 4 километра виден с высоты 0,00125 километра.
Ответ: 0,00125
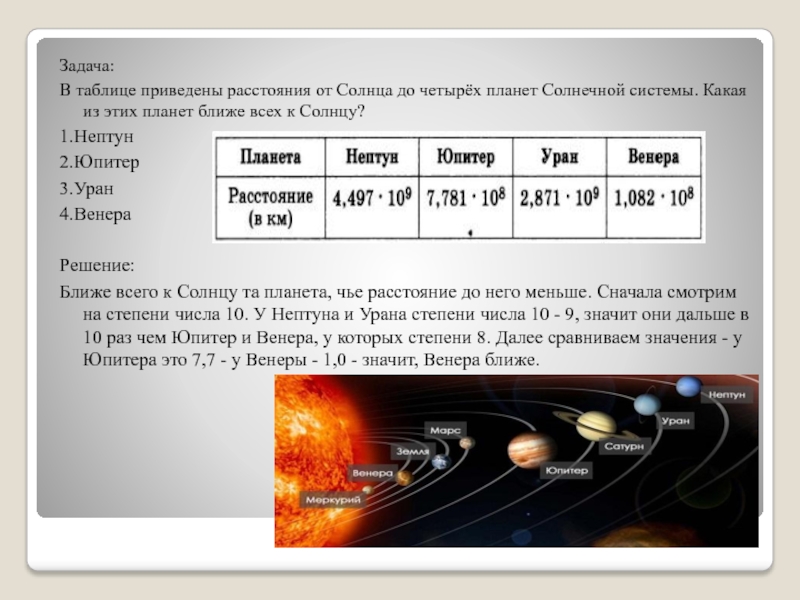
Слайд 30Задача:
В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы.
Какая из этих планет ближе всех к Солнцу?
1.Нептун
2.Юпитер
3.Уран
4.Венера
Решение:
Ближе всего к Солнцу
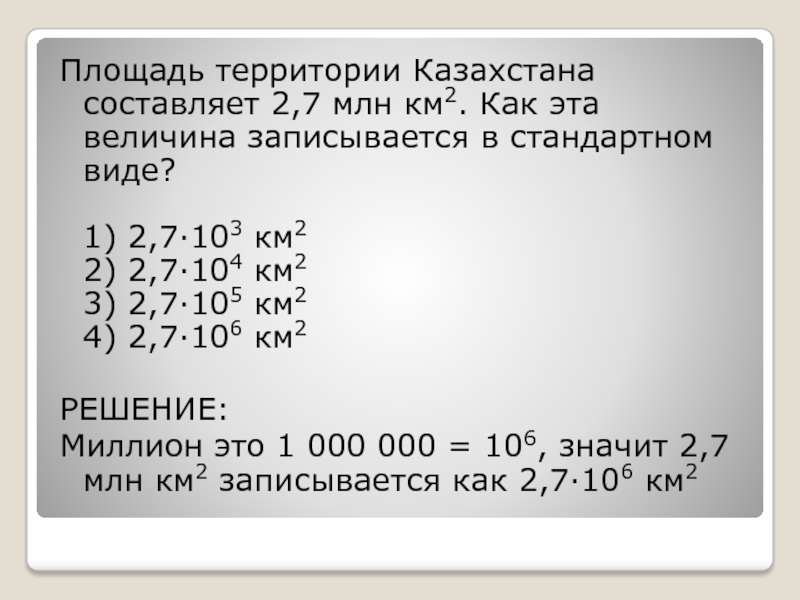
та планета, чье расстояние до него меньше. Сначала смотрим на степени числа 10. У Нептуна и Урана степени числа 10 - 9, значит они дальше в 10 раз чем Юпитер и Венера, у которых степени 8. Далее сравниваем значения - у Юпитера это 7,7 - у Венеры - 1,0 - значит, Венера ближе.
Слайд 32Площадь территории Казахстана составляет 2,7 млн км2. Как эта величина
записывается в стандартном виде?
1) 2,7·103 км2
2) 2,7·104 км2
3) 2,7·105 км2
4) 2,7·106 км2
РЕШЕНИЕ:
Миллион это 1
000 000 = 106, значит 2,7 млн км2 записывается как 2,7·106 км2
Слайд 33Условие:
В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы.
Какая из этих планет ближе всех к Солнцу?
Решение:
1,427•109=14,27•108, 4,497•109=44,97•108. Сравним
числа, наименьшим является число 2,28•108. 
Слайд 36Учащиеся умеют :
Привлекать и привлекают понятия и факты из родственных
дисциплин для расширения поля применимости теории, изучаемые в данном предмете
;Привлекать и привлекают теории, изученные на уроках других предметов ,для объяснения фактов, рассматриваемых в данной учебной дисциплине;
Привлекать и привлекают практически умения и навыки , полученные на уроках родственных дисциплин , для получения новых экспериментальных данных .
Слайд 37В завершении работы секции мы просим вас
выразить свое
настроение с
помощью одной из этих картинок
Интерес
Удовлетворение
Непонимание
Безразличие
Рефлексия:
