Множества и операции над ними

Содержание

1. Множества и операции над ними
2. «Множество есть многое, мыслимое нами как единое».
3. Понятие множества принадлежит к числу основных, неопределяемых
4. Объекты, составляющие данное множество, называют его
5. В математике часто исследуются так называемые числовые
6. Способы задания множестваперечисление элементов множества;
7. Поставьте вместо звездочки знак так,
8. Задайте перечислением элементов множество: 1) A
9. Действия над множествамиВключение и равенство множеств
10. Если для двух множеств Х и У
11. Объединение множеств ( сложение)Объединением А
12. Пересечение множеств Пересечением А ∩ В
13. Разность множеств Разностью А\В
14. Скачать презентанцию

«Множество есть многое, мыслимое нами как единое». Основоположник

Главная
Математика
Множества и операции над ними

Слайды и текст этой презентации

Слайд 1 Множества, операции над ними преподаватель математики МИПК им. И.Федорова Епихина

Е.В.

Слайд 2

«Множество есть многое, мыслимое нами как единое».

Основоположник

теории множеств немецкий математик
Георг Кантор
(1845-1918)

Слайд 3Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество

– набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для

всех их характеристическим свойством. Примеры множеств: множество студентов в данной аудитории; множество людей, живущих на нашей планете в данный момент времени; множество точек данной геометрической фигуры; множество чётных чисел; множество корней уравнения 5х+6=0;

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество – набор, совокупность, собрание каких-либо

Слайд 4 Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают

большими латинскими буквами, а элементы множества − малыми латинскими буквам.

Если элемент, а принадлежит множеству А, то пишут: а А Если а не принадлежит А, то пишут: а А.

Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают большими латинскими буквами, а

Слайд 5В математике часто исследуются так называемые числовые множества, т.е. множества,

элементами кото-рых являются числа. Для самых основных числовых множеств утвердились

следующие обозначения: N - множество всех натуральных чисел; Z - множество всех целых чисел; Q - множество всех рациональных чисел; R - множество всех действительных чисел. Приняты также обозначения Z+ , Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и Z¯, Q¯, R¯ -для множеств всех отрицательных целых, рациональных и действительных чисел.

В математике часто исследуются так называемые числовые множества, т.е. множества, элементами кото-рых являются числа. Для

Слайд 6Способы задания множества
перечисление элементов множества;

А={a; b; c; …;d}
указание характеристического

свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
А={х | 5х+6=0}.

Способы задания множестваперечисление элементов множества; А={a; b; c;

Слайд 7 Поставьте вместо звездочки знак так, чтобы полу-

чить правильное утверждение: 1) 5 * N;

2) –5 * Q; 3) 3,14 * Q; 4) 2 * R; 5) 0 * N; 6) − 12 * Z; 6) π * Q; 8) 3 * ∅

Поставьте вместо звездочки знак так, чтобы полу- чить правильное утверждение:

Слайд 8Задайте перечислением элементов множество: 1) A = {x | x

N, 2x – 1 = 0}; 2) B =

{x | x Z, | x | < 3}; 3) C = {x | x N, x ≤ 15, x = 7k, k Z}.

Задайте перечислением элементов множество: 1) A = {x | x N, 2x – 1 =

Слайд 9Действия над множествами
Включение и равенство множеств
Пусть Х и

У – два множества. Если каждый элемент х множества Х

является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У.

Действия над множествамиВключение и равенство множеств Пусть Х и У – два множества. Если каждый элемент

Слайд 10Если для двух множеств Х и У одновременно имеют место

два включения т.е. Х есть подмножество множества У и У

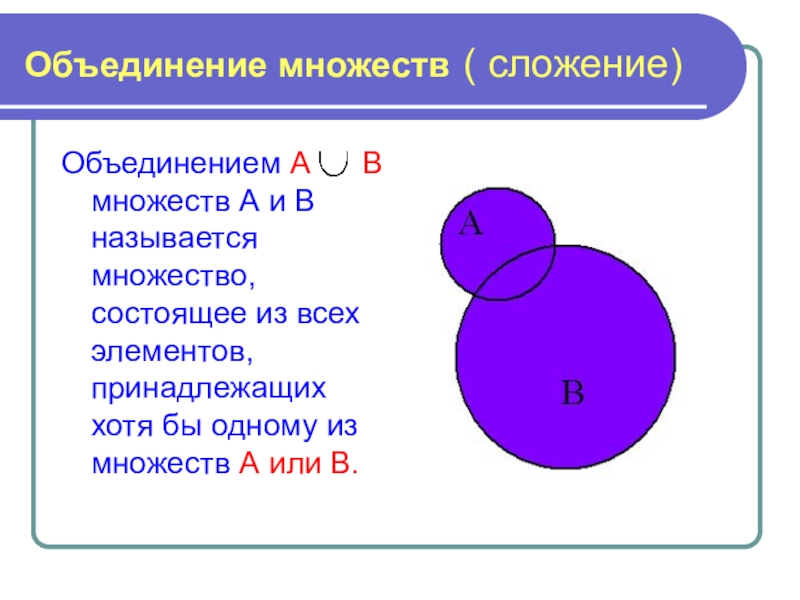
есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У.

Если для двух множеств Х и У одновременно имеют место два включения т.е. Х есть подмножество множества

Слайд 11Объединение множеств ( сложение)
Объединением А В множеств А

и В называется множество, состоящее из всех элементов, принадлежащих хотя

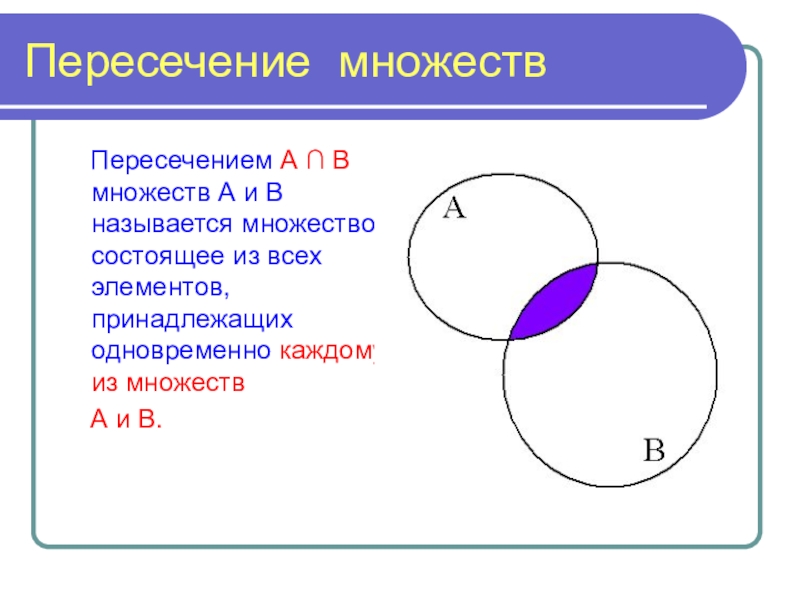
бы одному из множеств А или В.

Объединение множеств ( сложение)Объединением А В множеств А и В называется множество, состоящее из всех

Слайд 12Пересечение множеств
Пересечением А ∩ В множеств А и

В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому

из множеств
А и В.

Пересечение множеств Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов,

Слайд 13 Разность множеств
Разностью А\В множеств А и

В называется множество, состоящее из всех элементов множества А, которые

не принадлежат множеству В

$Разность множеств Разностью А\В множеств А и В называется множество, состоящее из всех элементов$

Скачать презентацию

Разделы презентаций

Множества и операции над ними

Содержание

Слайды и текст этой презентации

Слайд 1 Множества, операции над ними преподаватель математики МИПК им. И.Федорова Епихина

Е.В.

Слайд 2

«Множество есть многое, мыслимое нами как единое».

Основоположник

Слайд 3Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество

– набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для

Слайд 4 Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают

большими латинскими буквами, а элементы множества − малыми латинскими буквам.

Слайд 5В математике часто исследуются так называемые числовые множества, т.е. множества,

элементами кото-рых являются числа. Для самых основных числовых множеств утвердились

Слайд 6Способы задания множества
перечисление элементов множества;

А={a; b; c; …;d}
указание характеристического

Слайд 7 Поставьте вместо звездочки знак так, чтобы полу-

чить правильное утверждение: 1) 5 * N;

Слайд 8Задайте перечислением элементов множество: 1) A = {x | x

N, 2x – 1 = 0}; 2) B =

Слайд 9Действия над множествами
Включение и равенство множеств
Пусть Х и

У – два множества. Если каждый элемент х множества Х

Слайд 10Если для двух множеств Х и У одновременно имеют место

два включения т.е. Х есть подмножество множества У и У

Слайд 11Объединение множеств ( сложение)
Объединением А В множеств А

и В называется множество, состоящее из всех элементов, принадлежащих хотя

Слайд 12Пересечение множеств
Пересечением А ∩ В множеств А и

В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому

Слайд 13 Разность множеств
Разностью А\В множеств А и

В называется множество, состоящее из всех элементов множества А, которые

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Множества и операции над ними

Содержание

Слайды и текст этой презентации

Слайд 1 Множества, операции над ними преподаватель математики МИПК им. И.Федорова Епихина

Е.В.

Слайд 2«Множество есть многое, мыслимое нами как единое».

Основоположник

Слайд 3Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество

– набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для

Слайд 4 Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают

большими латинскими буквами, а элементы множества − малыми латинскими буквам.

Слайд 5В математике часто исследуются так называемые числовые множества, т.е. множества,

элементами кото-рых являются числа. Для самых основных числовых множеств утвердились

Слайд 6Способы задания множестваперечисление элементов множества;

А={a; b; c; …;d} указание характеристического

Слайд 7 Поставьте вместо звездочки знак так, чтобы полу-

чить правильное утверждение: 1) 5 * N;

Слайд 8Задайте перечислением элементов множество: 1) A = {x | x

N, 2x – 1 = 0}; 2) B =

Слайд 9Действия над множествамиВключение и равенство множеств Пусть Х и

У – два множества. Если каждый элемент х множества Х

Слайд 10Если для двух множеств Х и У одновременно имеют место

два включения т.е. Х есть подмножество множества У и У

Слайд 11Объединение множеств ( сложение)Объединением А В множеств А

и В называется множество, состоящее из всех элементов, принадлежащих хотя

Слайд 12Пересечение множеств Пересечением А ∩ В множеств А и

В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому

Слайд 13 Разность множеств Разностью А\В множеств А и

В называется множество, состоящее из всех элементов множества А, которые

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 2

«Множество есть многое, мыслимое нами как единое».

Слайд 6Способы задания множества
перечисление элементов множества;

А={a; b; c; …;d}
указание характеристического

Слайд 9Действия над множествами
Включение и равенство множеств
Пусть Х и

Слайд 11Объединение множеств ( сложение)
Объединением А В множеств А

Слайд 12Пересечение множеств
Пересечением А ∩ В множеств А и

Слайд 13 Разность множеств
Разностью А\В множеств А и