Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неравинства
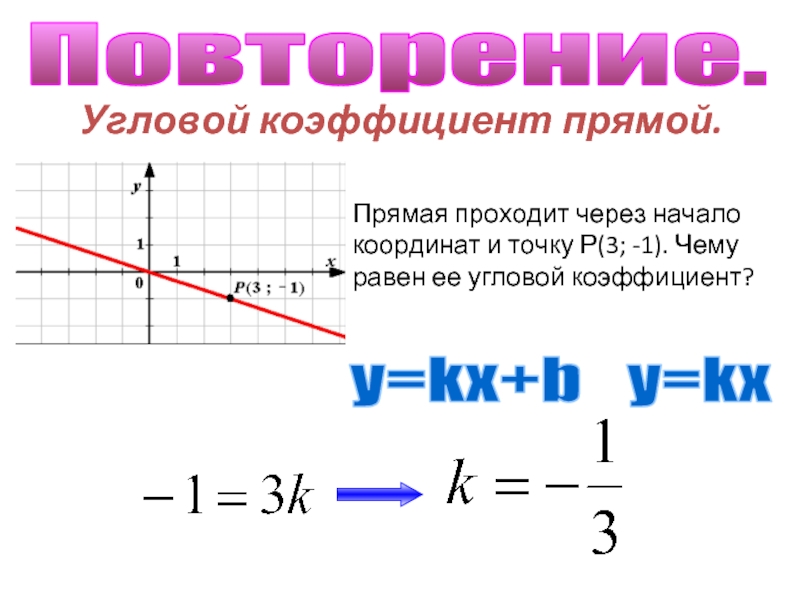
Содержание
- 1. Неравинства
- 2. ВВЕДЕНИЕ Готовя данную работу, я ставила
- 3. ИСТОРИЧЕСКИЕ СВЕДЕНИЯАрхимед указал границы числа ∏ :
- 4. ЧИСЛОВЫЕ НЕРАВЕНСТВАДля произвольных чисел a и b
- 5. ПРИМЕРЫСравним 5/8 и 4/7. Приведём их к
- 6. СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВЕсли a>b, то b
- 7. Сложение и умножение числовых неравенствЕсли a
- 8. Решение неравенств с одной переменнойРешением неравенства
- 9. Решение систем неравенств с одной переменнойРешением системы
- 10. ПРИМЕРЫРешим неравенство 16х>13х+45. Перенесем слагаемое 13х
- 11. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА Рациональные неравенств – это неравенства вида Pn(x)/Qm(x)>0(≥,
- 12. ПРИМЕРЫ ПРИМЕР .Множество решений неравенства (x²
- 13. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА Основным методом решения
- 14. ПРИМЕРЫПРИМЕР . Решить неравенство (x-1)√x²-x-2≥0. D(f)=(-∞;-1]U[2;+∞).Х - 1≥0;Х=1; Х>2;Ответ: Х=1; Х>2.
- 15. ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВАДва тригонометрических выражения, соединённых между собой знаками «>» или «
- 16. ПРИМЕРЫ Решим
- 17. НЕРАВЕНСТВА С МОДУЛЯМИ При решении неравенств, содержащих
- 18. ПРИМЕРЫ Пример. Решить неравенство |х - 1|
- 19. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
- 20. ПРИМЕРЫ Пример . Решить неравенство 3х+7
- 21. НЕРАВЕНСТВА С ПАРАМЕТРАМИ. Неравенство (a,
- 22. ПРИМЕРЫ Пример. Найти значение параметра а,
- 23. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА При решении неравенств вида
- 24. ПРИМЕРЫ ПРИМЕР. Решить неравенство Log1/3 (2x+59)>-2.
- 25. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
- 26. ПРИМЕРЫ ПРИМЕР. Изобразить на координатной плоскости множество решений неравенства x+y-1>0.y>-x+1 ;
- 27. ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВТРИ МЕТОДА ДОКАЗАТЕЛЬСТВ НЕРАВЕНСТВ:1)Метод оценки знака разности; 2) Синтетический метод;3) Метод от противного.
- 28. Скачать презентанцию
ВВЕДЕНИЕ Готовя данную работу, я ставила цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. В моём реферате рассмотрены часто встречающиеся типы неравенств и их
Слайды и текст этой презентации
Слайд 3ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
Архимед указал границы числа ∏ :
223/7122/7.
В «Математике собрании» Паппа Александрийского(||| в.)
доказывается, что если a/b>c/d (a,b,c,d – положительные числа), то ad>bc. Знаки< и > ввёл английский математик Т. Гарриот (1560-1621), знаки ≤ и ≥ французский математик П. Буге (1698-1758).
Слайд 4ЧИСЛОВЫЕ НЕРАВЕНСТВА
Для произвольных чисел a и b выполняется одно и
только одно из соотношений: a=b, ab.
Число a больше
числа b, если разность a-b - положительное число; число a меньше числа b, если разность a-b - отрицательное число.Слайд 5ПРИМЕРЫ
Сравним 5/8 и 4/7. Приведём их к общему знаменателю: 5/8=35/56;
4/7=32/56. Так как 35>32, то 5/8>4/7.
Докажем, что при любых значениях
a верно неравенство (a-3)(a-5)<(a-4)(a-4). Составим разность левой и правой частей неравенства и преобразуем её: (a-3)(a-5)-(a-4)(a-4)=-1. При любом a верно данное неравенство.Слайд 6СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ
Если a>b, то b
a
то a+cЕсли a и b - положительные числа и a 1/b.
Слайд 8 Решение неравенств с одной переменной
Решением неравенства с одной переменной
называется значение переменной, которое обращает его в верное числовое неравенство.
Если
из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.
Слайд 9Решение систем неравенств с одной переменной
Решением системы неравенств с одной
переменной называется значение переменной, при котором верно каждое из неравенств
системы.Решить систему - значит найти все её решения или доказать, что решений нет.
Слайд 10ПРИМЕРЫ
Решим неравенство 16х>13х+45. Перенесем слагаемое 13х с противоположным знаком
в левую часть неравенства: 16х-13х>45. Приведём подобные члены: 3х>45. Умножим
обе части на 1/3 : х>15.Решим неравенство х/3 - х/2<2 . Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство, т.е. на 6. Получим: 6х/3 – 6х/2<12; 2х – 3х<12. Отсюда -х<12; х> -12.
Слайд 11РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Рациональные неравенств – это неравенства вида Pn(x)/Qm(x)>0(≥,
где Pn(x) и Qm(x) – многочлены степеней n и m
соответственно. Основной метод решения рациональных неравенств – метод интервалов.Слайд 12ПРИМЕРЫ
ПРИМЕР .Множество решений неравенства (x² -7x+12)/(2x²+4x+5)>0 имеет вид
1)(-∞; 3)U(4; ∞) 2) (-∞; 3) 3) (3; 4)
4) (4; ∞) 5) (-∞;4).РЕШЕНИЕ. Так как дискриминант знаменателя D1=4²-4*5*2 отрицателен и старший коэффициент положителен, то 2x²+4x+5>0 для любого значения x. Тогда заданное неравенство равносильно неравенству x²-7x+12>0 или (x-3)(x-4)>0.
Отметим корни и знаки квадратного трёхчлена
x²-7x+12 на соответствующих промежутках числовой оси.
Решением неравенства является множество (-∞; 3)U(4; ∞).
ОТВЕТ: 1.
Слайд 13ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Основным методом решения иррациональных неравенств
является метод сведения исходного неравенства к равносильной системе рациональных неравенств
или совокупности таких систем.Слайд 14ПРИМЕРЫ
ПРИМЕР . Решить неравенство
(x-1)√x²-x-2≥0.
D(f)=(-∞;-1]U[2;+∞).
Х - 1≥0;
Х=1; Х>2;
Ответ: Х=1;
Х>2.
Слайд 15ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Два тригонометрических выражения, соединённых между собой знаками «>» или
«
найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.Слайд 16ПРИМЕРЫ
Решим неравенство sinх>1/2. Все
значения у на промежутке NM больше 1/2. NM стягивает дугу
AB с началом в точке А(п/6; ½) и с концом в точке B(5п/6; ½). Следовательно, решением неравенства будут все значения на (п/6; 5п/6) с прибавлением 2пn, т.е. п/6+2пn<х< 5п/6+2пn, n принадлежит Z.Слайд 17НЕРАВЕНСТВА С МОДУЛЯМИ
При решении неравенств, содержащих переменные под знаком
модуля, используется определение модуля:
f(х),
если f(х)≥0,|f(х)|=
- f(х), если f(х)<0.
Слайд 18ПРИМЕРЫ
Пример. Решить неравенство |х - 1|
помощью координатной прямой устанавливаем, что множество решений неравенства есть интервал
( - 1; 3).
Слайд 19ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
f(x) g(x)
При решении неравенств вида а>а следует помнить, что х
показательная функция у=а возрастает при а>0 и убывает при
0
В случае же, когда 0
Слайд 20ПРИМЕРЫ
Пример . Решить неравенство 3х+7 2х -
1
2 < 2.Решение. Здесь основание степени больше 1, поэтому, сравнивая показатели, запишем неравенство того же смысла: 3х+7<2x – 1.
3х – 2х<-1 – 7;
х< - 8;
Ответ: х< - 8.
Слайд 21НЕРАВЕНСТВА С ПАРАМЕТРАМИ.
Неравенство
(a, b, c,
…, k , x)> (a, b, c, …, k ,
x),где a, b, c, …, k – параметры, а x действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.
Слайд 22ПРИМЕРЫ
Пример. Найти значение параметра а, при котором наименьшее
решение неравенства (ах – 10)/х≥1 равно -2.
Решение. (ах
– 10)/х – 1≥0 => ((а – 1)х – 10)/х≥0 => (а – 1)(х – 10/(а – 1))/х≥0. Пусть а – 1>0. Тогда последнее неравенство пишется в виде ( х – 10/(а – 1))/х≥0. Его решением является объединение множеств (-∞; 0)U[10/(а – 1); +∞], которое не содержит наименьшего отрицательного числа. Следовательно, а – 1<0 и тогда решением неравенства будет множество [10/(а – 1); 0). 10/(а – 1)=2; а – 1=5; а=-4.Слайд 23ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
При решении неравенств вида Logaf(x)>Loga g(x) следует
помнить, что логарифмическая функция y=Logax возрастает при a>1 и убывает
при 0Слайд 24ПРИМЕРЫ
ПРИМЕР. Решить неравенство Log1/3 (2x+59)>-2.
РЕШЕНИЕ. Так
как -2=Log1/3 9, то данное неравенство можно переписать в виде
Log1/3 (2x+59)>Log1/3 9.Далее имеем:
2x+59>0, x>-29,5,
2x+59<9; x<-25;
откуда -29,5













![Неравинства ПРИМЕРЫПРИМЕР . Решить неравенство (x-1)√x²-x-2≥0. D(f)=(-∞;-1]U[2;+∞).Х - 1≥0;Х=1; Х>2;Ответ: Х=1; Х>2. ПРИМЕРЫПРИМЕР . Решить неравенство (x-1)√x²-x-2≥0. D(f)=(-∞;-1]U[2;+∞).Х - 1≥0;Х=1; Х>2;Ответ: Х=1; Х>2.](/img/thumbs/df22cc4bdebc55ba864ba253a08eadcb-800x.jpg)