Нестандартные способы решения задач на смеси и сплавы

или смеси однородны.

При решении этих задач считается, что масса смеси

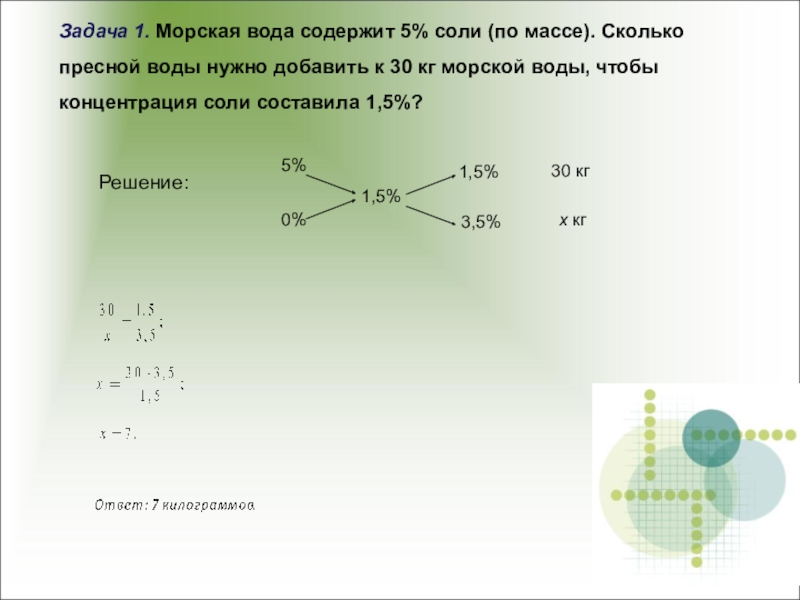
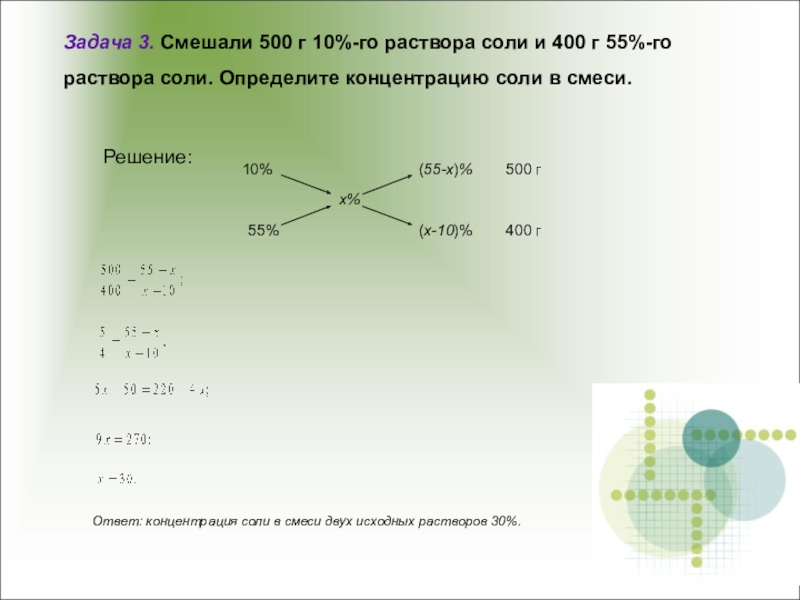
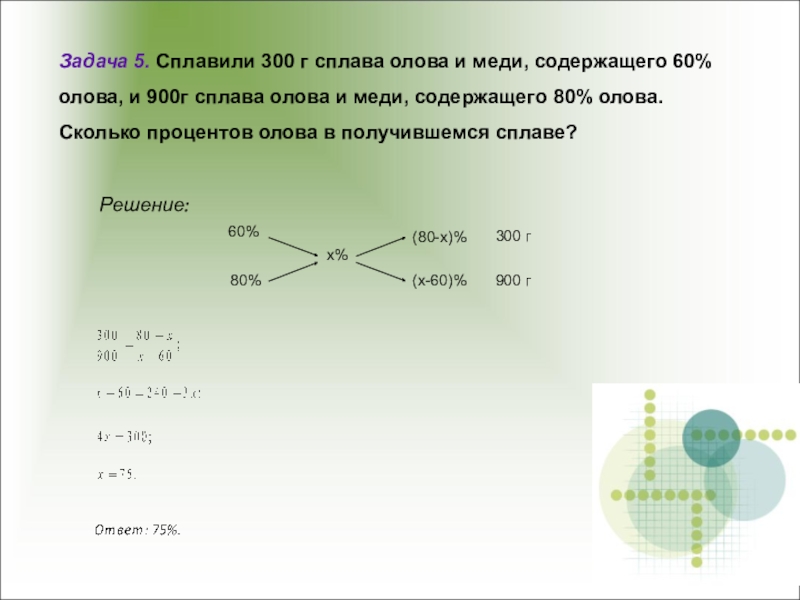
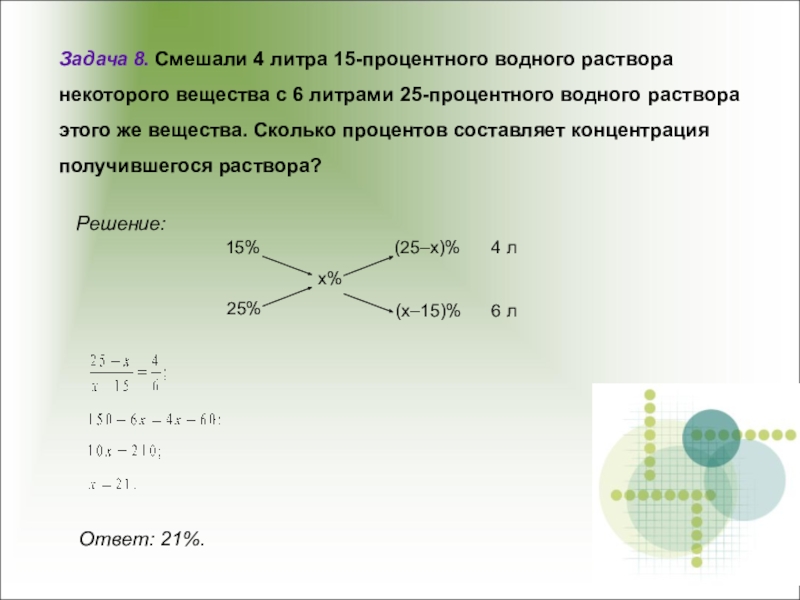
нескольких веществ равна сумме масс компонентов.

Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.

Терминология:

процентное содержание вещества;
концентрация вещества;
массовая доля вещества. Всё это синонимы.

раствора с более высокой и менее высокой концентрацией, чем нужно.
Если

обозначить массу первого раствора через m 1, а второго – через m 2, то при смешивании общая масса смеси будет складываться из суммы этих масс.
Пусть массовая доля растворённого вещества в первом растворе – ω 1, во втором – ω 2, а в их смеси – ω 3. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:
m 1 ω 1 + m 2 ω 2 = ω 3(m 1 + m 2),
m 1(ω 1 – ω 3) = m 2(ω 3 – ω 2),


Очевидно, что отношение массы первого раствора к массе
второго раствора есть отношение разности массовых долей растворённого
вещества в смеси и во втором растворе к разности соответствующих
величин в первом растворе и в смеси.

Правило креста или квадрат Пирсона

применяют диагональную схему правила смешения или квадрат Пирсона.
При расчётах записывают

одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

ω1 ω3 — ω2
ω3
ω2 ω1 — ω3

пресной воды нужно добавить к 30 кг морской воды, чтобы

концентрация соли составила 1,5%?


Решение:

5%

0%

1,5%

1,5%

3,5%

30 кг

х кг

2 литра жидкости и долили 2 литра 45% раствора этой

же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд?


Решение:
97%
81%

45%

16%

36%

(х-2) л

2 л

г 55%-го раствора соли. Определите концентрацию соли в смеси.


Решение:

Ответ: концентрация соли в смеси двух исходных растворов 30%.

(х-10)%

(55-х)%

500 г

400 г

55%

10%

х%

на 3 кг больше, чем масса первого слитка. Процентное содержание

меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка.

Решение:

40%

10%

30%

10%

20%

(х+3) кг

х кг

60% олова, и 900г сплава олова и меди, содержащего 80%

олова. Сколько процентов олова в получившемся сплаве?

Решение:

60%

80%

х%

(х-60)%

(80-х)%

300 г

900 г

водного
раствора некоторого вещества, добавили 7 литров воды. Сколько
процентов составляет концентрация

получившегося раствора?

Решение:

х%

12%

0%

х%

(12–х)%

5 л

7 л

же количеством 19-процентного раство-
ра этого вещества. Сколько процентов составляет концентрация
получившегося

раствора?

Решение:

Ответ: 17%.

15%

19%

х%

(19–х)%

(х–15)%

т г

т г

с 6 литрами 25-процентного водного раствора этого же вещества. Сколько

процентов составляет концентрация получившегося раствора?

Решение:













Ответ: 21%.

15%

25%

х%

(25–х)%

(х–15)%

4 л

6 л

содержит 10% никеля,
второй — 30% никеля. Из этих двух сплавов

получили третий
сплав массой 200 кг, содержащий 25% никеля. На сколько
килограммов масса первого сплава меньше массы второго?

Решение:

(кг) – 1-й сплав;

(кг) – 2-й сплав;

(кг) – разница.

Ответ: на 100 кг.

10%

30%

25%

5%

15%

х кг

(200–х) кг

1)

2)

3)

меди. Масса второго сплава больше массы первого на 3 кг.

Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение:

(кг) — 1-й сплав;

(кг) — 2-й сплав;

(кг) — 3-й сплав.

10%

40%

30%

10%

20%

х кг

(х+3) кг

1)

2)

3)

Ответ: 9 кг.

мёдом. По его ощущениям этот мёд, к сожалению, только лишь

на одну пятую часть правильный (остальные четыре пятые – неправильные). В дупле же, найденном по дороге ОБРАТНО, мёд на 60% правильный. Сколько килограммов мёда нужно взять из первого и второго(10 – Х) кг дупла, чтобы в общей сложности получить 10 кг меда, содержащего 32% правильного?

Решение:

Ответ: 7 килограммов из первого и 3 килограмма из второго дупла.