Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обратные тригонометрические функции
Содержание
- 1. Обратные тригонометрические функции
- 2. Содержание:Обратные тригонометрические функции, свойства, графикиИсторическая справка Преобразование выражений, содержащих обратные тригонометрические функцииРешение уравненийЗадания различного уровня сложности
- 3. Из истории тригонометрических функцийДревняя Греция.III в до
- 4. Arcsin
- 5. Свойства функции y = arcsin x 1)Область
- 6. Arccos
- 7. Функция y= arccosx является строго убывающейcos(arccosx) =
- 8. ArctgхАрктангенсом
- 9. y=arctgх1)Область
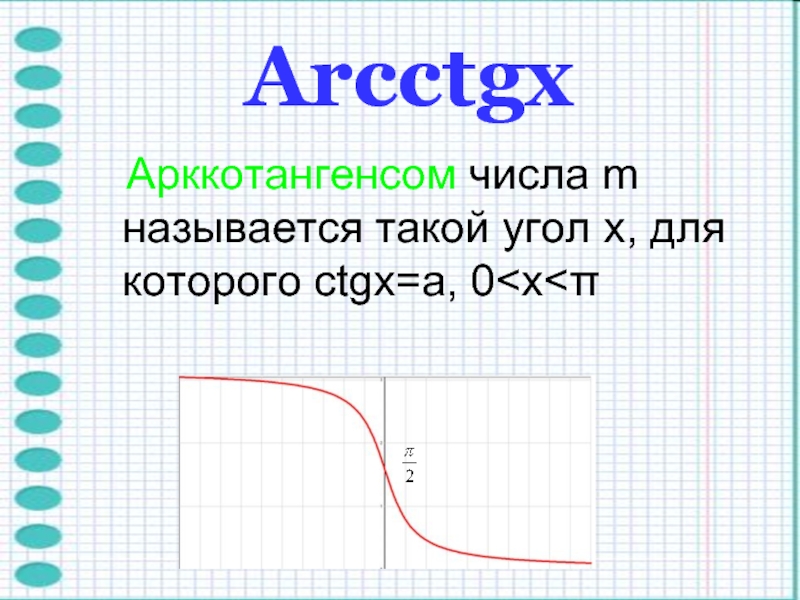
- 10. Arcctgх Арккотангенсом
- 11. Функция y=arcctgx непрерывна и ограничена на всей
- 12. Преобразование выражений
- 13. Преобразование выражений
- 14. Слайд 14
- 15. Уравнения, содержащиеобратные тригонометрические функции
- 16. Упражнения для самостоятельного решения
- 17. Задания различного уровня сложности
- 18. Задания различного уровня сложности
- 19. Задания различного уровня сложности
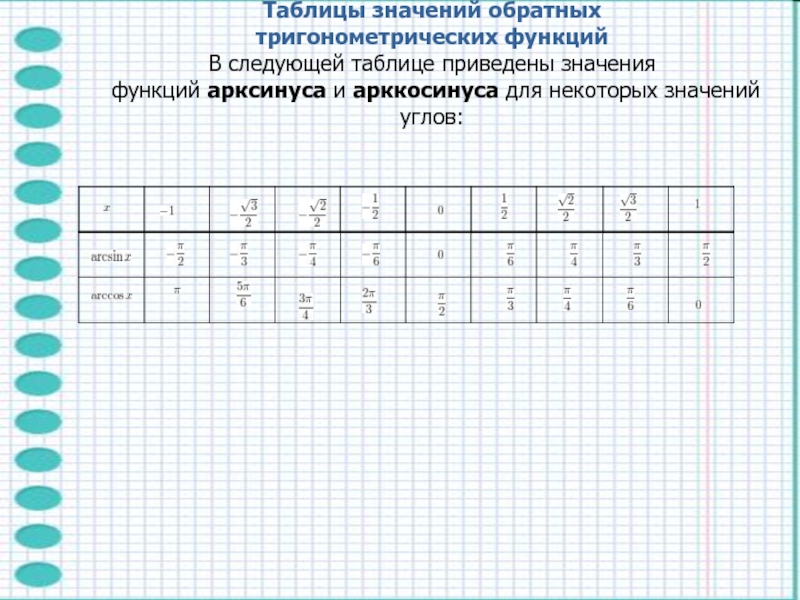
- 20. Таблицы значений обратных тригонометрических функцийВ следующей таблице приведены значения функций арксинуса и арккосинуса для некоторых значений углов:
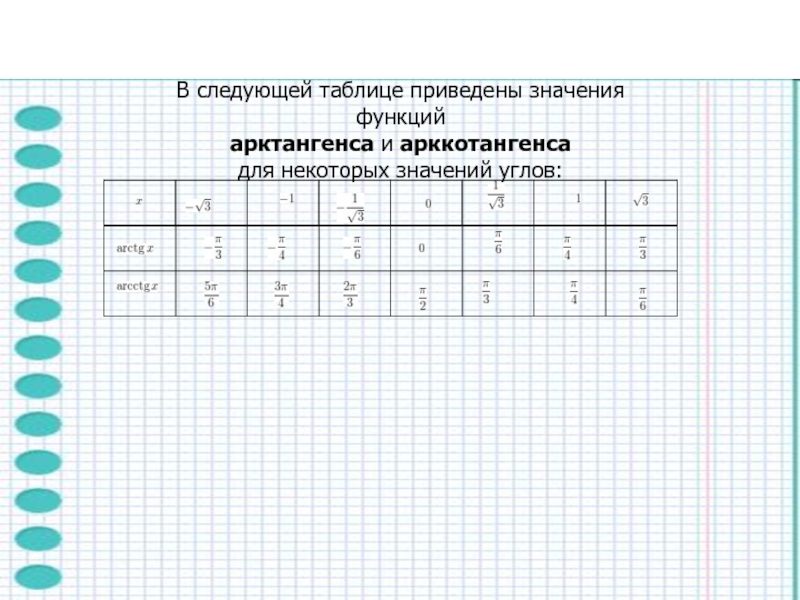
- 21. В следующей таблице приведены значения функций арктангенса и арккотангенса для некоторых значений углов:
- 22. Литература:Алгебра и начала анализа: учеб. Для 10-11
- 23. Скачать презентанцию
Содержание:Обратные тригонометрические функции, свойства, графикиИсторическая справка Преобразование выражений, содержащих обратные тригонометрические функцииРешение уравненийЗадания различного уровня сложности
Слайды и текст этой презентации
Слайд 2Содержание:
Обратные тригонометрические функции, свойства, графики
Историческая справка
Преобразование выражений, содержащих обратные
тригонометрические функции
Слайд 3Из истории тригонометрических функций
Древняя Греция.III в до н. э. Евклид,
Аполоний Пергский. Отношения
сторон в прямоугольном треугольнике.
Ок. 190 до н.
э Гиппарх Никейский. Возможно он первый составилтаблицу хорд, аналог современных таблиц тригонометрических функций.
Абу-аль-Ваф ввел тригонометрические функции тангенс и котангенс.
Первая половина XV в. Аль-Каши произвел уникальные расчеты, которые
были нужны для составления таблицы синусов с шагом 1’.
I-II вв. индийские математики вводят понятие синуса.
1423-1461- австрийский математик и астроном Георг фон Пойербах
был одним из первых европейских ученых, которрый применил
понятие синуса.
1602-1675 французский математик, астроном и физик Жиль Роберваль
построил синусоиду.
XV в. Региомонтан ввел термин тангенс.
1739 г. И. Бернулли ввел современные обозначения синуса и косинуса.
1770 г. Георг Симон Клюгель вводит новый термин тригонометрические
функции.
1772 г. Ж. Лагранж вводит первую из шести обратных тригонометрических
функций.
Карл Шерфер ввел современные обозначения для обратных
тригонометрических функций.
Слайд 4 Arcsin х
Арксинусом числа m
называется такой угол x, для которого sinx=m, -π/2≤X≤π/2,|m|≤1
Функция y =
sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.График обратной функции симметричен с графиком основной функции относительно биссектрисы I - III координатных углов.
Слайд 5Свойства функции y = arcsin x
1)Область определения: отрезок [-1;
1];
2)Область изменения: отрезок [-π/2,π/2];
3)Функция y
= arcsin x нечетная: arcsin (-x) = - arcsin x;4)Функция y = arcsin x монотонно возрастающая;
5)График пересекает оси Ох, Оу в начале координат.
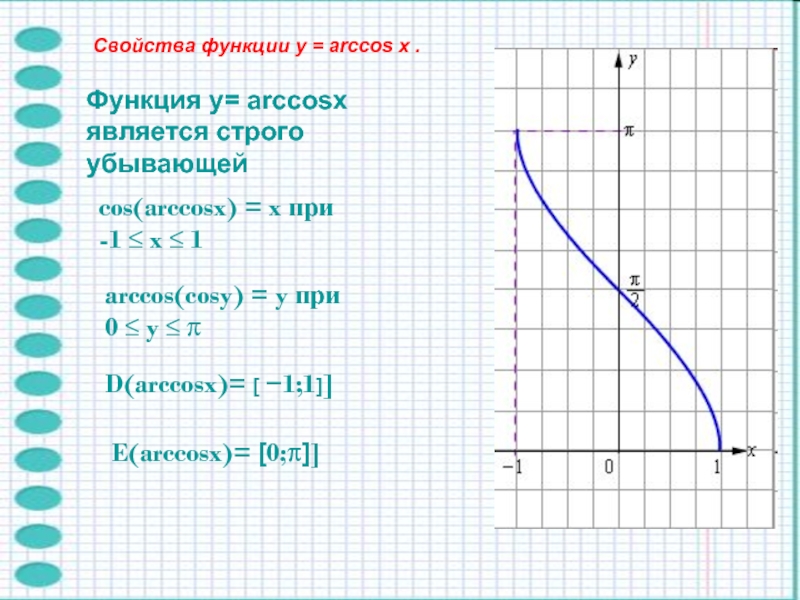
Слайд 7Функция y= arccosx является строго убывающей
cos(arccosx) = x при
-1
≤ x ≤ 1
arccos(cosy) = y при
0 ≤ y
≤ πD(arccosx)= [ −1;1]]
E(arccosx)= [0;π]]
Свойства функции y = arccos x .
Слайд 8 Arctgх
Арктангенсом числа m
называется
такой угол x,
для которого tgx=m,
-π/2
графика Функции y=tgx, симметрией
Относительно прямой y=x.
Слайд 9 y=arctgх
1)Область определения: R
2)Область
значения: отрезок [-π/2,π/2];
3)Функция y = arctg
x нечетная: arctg (-x) = - arctg x;4)Функция y = arctg x монотонно возрастающая;
5)График пересекает оси Ох, Оу в начале координат.
y
y
x
Слайд 11Функция y=arcctgx непрерывна и ограничена на всей своей числовой прямой.
Функция y=arcctgx является строго убывающей.
ctg(arcctgx)=x при xєR
arcctg(ctgy)=y при 0
y < πD(arcctgx)=(-∞;∞)
E(arcctgx)=(0; π)
Arcctgх




![Обратные тригонометрические функции Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; 2)Область изменения: отрезок](/img/thumbs/d2a7c9dcc5b7304c5a5bb390465232ec-800x.jpg)


![Обратные тригонометрические функции y=arctgх1)Область определения: R 2)Область значения: отрезок y=arctgх1)Область определения: R 2)Область значения: отрезок [-π/2,π/2];3)Функция](/img/thumbs/503d7f4fe81f83208ce48f52215a44f2-800x.jpg)