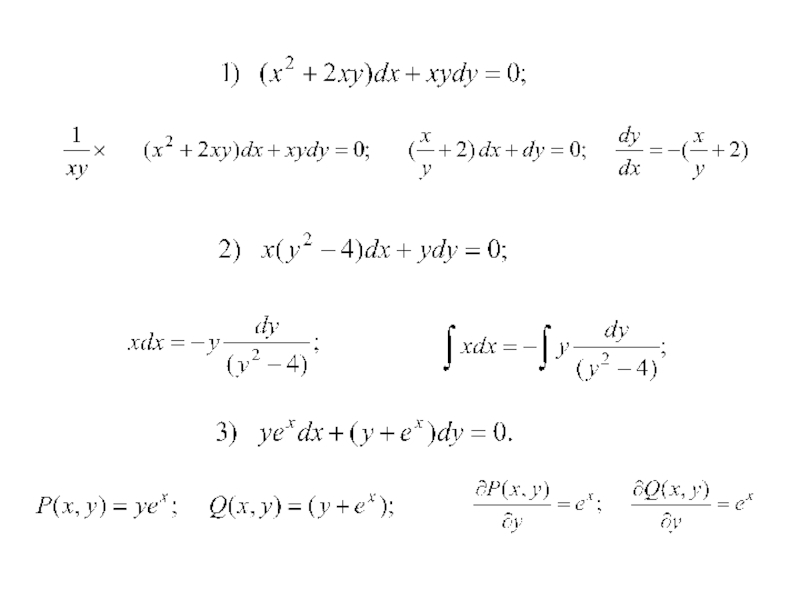значения независимой переменной x, неизвестной функции y = f(x) и
её производных (или дифференциалов):Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Пример: y(4) – y + x = 0 - уравнение четвёртого порядка.
Функция y(x) называется решением (или интегралом) дифференциального уравнения если при подстановке ее в уравнение обращает его в тождество.