Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Осевая симметрия. Центральная симметрия. Симметрия вокруг нас
Содержание
- 1. Осевая симметрия. Центральная симметрия. Симметрия вокруг нас
- 2. Слайд 2
- 3. СимметрияСимметрия — слово греческого происхождения. Оно
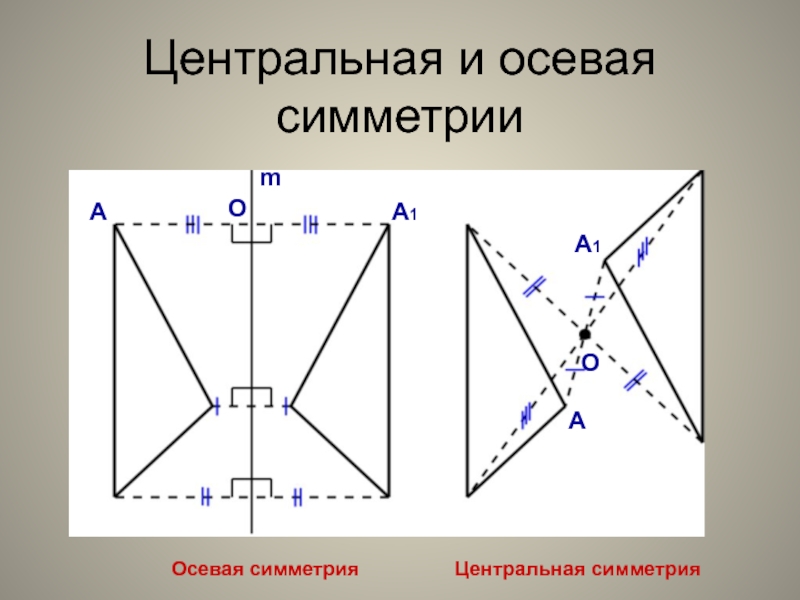
- 4. Центральная и осевая симметрииОсевая симметрияЦентральная симметрияАА1ОmАА1О
- 5. Осевая симметрия — это симметрия относительно
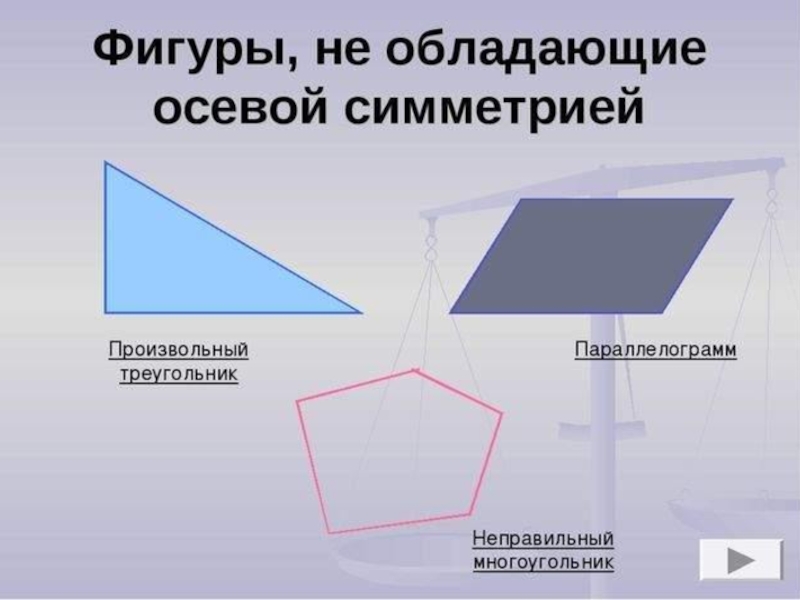
- 6. Фигура называется симметричной относительно прямой а, если
- 7. Слайд 7
- 8. Алгоритм построения фигуры, симметричной относительно некоторой прямой.Построим
- 9. Слайд 9
- 10. Симметрию относительно точки называют центральной симметрией.Точки M
- 11. Понятие «центральная симметрия» фигуры предполагает существование определенной
- 12. Фигуры обладающие центральной симметрией
- 13. С симметрией мы часто встречаемся в искусстве,
- 14. Примеры симметрии в живописи
- 15. Симметричной композицией можно назвать «Тайную вечерю» Леонардо
- 16. Слайд 16
- 17. Картина В. М. Васнецова «Богатыри» также построена
- 18. Слайд 18
- 19. Но симметрия широко распространена и в природе,
- 20. Центральная симметрия наиболее характерна для цветов и
- 21. Центральную симметрию можно наблюдать на изображении
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. СИММЕТРИЯ РЯДОМ С НАМИДЕВОЧКАМ: симметрия в прическе является важным средством достижения художественной выразительности.
- 26. СПАСИБО ЗА ВНИМАНИЕ!Выполнил Сумин Данил Александрович 8 «Б»Новомичуринская СОШ №2Учитель И.В.Ильченко
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3 Симметрия
Симметрия — слово греческого происхождения. Оно означает соразмерность, наличие
определённого порядка, закономерности в расположении частей, свойство геометрических объектов совмещаться
с собой при определенных преобразованиях. Под симметрией понимают всякую правильность во внутреннем строении тела или фигуры. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»Слайд 5
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M
и M1 симметричны относительно некоторой прямой (оси симметрии), если
эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии. Прямая а является осью симметрии.а
Слайд 6Фигура называется симметричной относительно прямой а, если для каждой точки
фигуры симметричная ей точка относительно прямой а также принадлежит этой
фигуре.А1
Окружность с центром в точке О и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые: m, m1, m2, m3 ...
Квадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s. Если квадрат перегнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
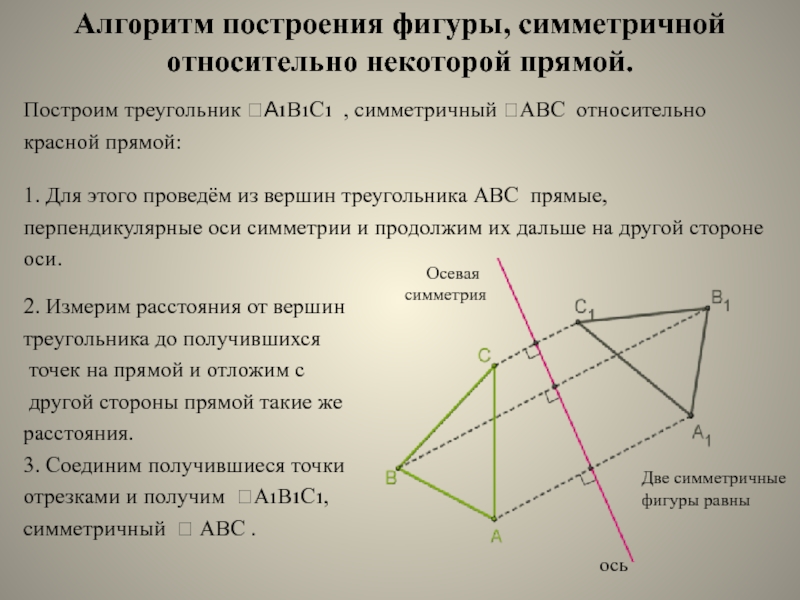
Слайд 8Алгоритм построения фигуры, симметричной относительно некоторой прямой.
Построим треугольник А1В1С1 ,
симметричный ABC относительно красной прямой:
1. Для этого проведём из вершин
треугольника ABC прямые, перпендикулярные оси симметрии и продолжим их дальше на другой стороне оси. 2. Измерим расстояния от вершин
треугольника до получившихся
точек на прямой и отложим с
другой стороны прямой такие же
расстояния.
3. Соединим получившиеся точки
отрезками и получим A1B1C1,
симметричный ABC .
ось
Осевая симметрия
Две симметричные фигуры равны
Слайд 10Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны
относительно некоторой точки O , если точка O является серединой
отрезка MM1.Точка O называется центром симметрии
Слайд 11Понятие «центральная симметрия» фигуры предполагает существование определенной точки – центра
симметрии. По обе стороны от него располагаются точки, принадлежащие этой
фигуре. Каждая из них имеет симметричную себе. Центральная симметрия присутствует в таких известных всем фигурах, как параллелограмм и окружность. И у первой, и у второй фигуры центр один. Центр симметрии параллелограмма расположен в точке пересечения прямых, вышедших из противоположных точек; в окружности – это центр ее самой. Для прямой характерно наличие бесконечного количества таких участков. Каждая ее точка может являться центром симметрии.Слайд 13С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту.
Фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны
относительно оси или центра узоры на коврах, тканях, комнатных обоях.Слайд 15Симметричной композицией можно назвать «Тайную вечерю» Леонардо да Винчи. В
этой фреске показан драматический момент, когда Христос сообщил своим ученикам:
«Один из вас предаст меня». Психологическая реакция апостолов на эти вещие слова связывает персонажей с композиционным центром, в котором находится фигура Христа. Впечатление целостности от этой центростремительной композиции усиливается еще и тем, что художник показал помещение трапезной в перспективе с точкой схода параллельных линий в середине окна, на фоне которого четко рисуется голова Христа. Таким образом, взор зрителя невольно направляется к центральной фигуре картины.Слайд 17Картина В. М. Васнецова «Богатыри» также построена на основе правила
симметрии. В картине по небу движутся тяжелые облака, колышется спелая
нива, волнуются могучие кони, с трепещущими от ветра гривами. Сами герои полны сдерживаемой силы: вся группа чуть сдвинута влево, один из богатырей выдвигает меч, другой прикрывает ладонью глаза, третий, наклонив голову, прислушивается. Центром композиции является фигура Ильи Муромца. Слева и справа, как бы в зеркальном отражении, размещены Алеша Попович и Добрыня Никитич. Фигуры расположены вдоль картинной плоскости спокойно сидящими на конях. Симметричное построение композиции передает состояние относительного покоя. Левая и правая фигуры по массам неодинаковы, что обусловлено идейным замыслом автора. Но обе они менее мощные по сравнению с фигурой Муромца и в целом придают полное равновесие композиции.Устойчивость композиции вызывает у зрителя чувство уверенности в непобедимости богатырей, защитников земли русской. Мало того, в «Богатырях» передано состояние напряженного покоя на грани перехода в действие. А это значит, что и симметрия несет в себе зародыш динамического движения во времени и пространстве.