Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Отыскание наибольшего и наименьшего значений непрерывной функции
Содержание
- 1. Отыскание наибольшего и наименьшего значений непрерывной функции
- 2. Слайд 2
- 3. Структура урока
- 4. Задание 1. Найдите производную функции:Ход урока:Организационный момент.Устная работа (для всего класса с помощью проектора предлагается разминка)
- 5. Задание 2. Вычислите значение функции:
- 6. Задание 3 .Найдите промежутки возрастания и убывания функции:Решение:0,3+-функция убываетфункция возрастает
- 7. Задание 3 .Найдите промежутки возрастания и убывания функции:Решение:+--6функция убываетфункция возрастает
- 8. Задание 4 .Найдите точки экстремума функции:Решение:-+1
- 9. 3. Изучение нового материала.Русский математик XIX века
- 10. Здесь возможны варианты – рассмотрим их по
- 11. Алгоритм отыскания наименьшего и наибольшего значений непрерывной
- 12. 4. Закрепление нового материала.Найдите наименьшее
- 13. 4. Подведение итога урока. Выставление
- 14. Спасибо за урок. До свидания.
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Цели урока: 1) изучить понятие наибольшего и наименьшего значения функции; 2) изучить алгоритм вычисления наибольшего и наименьшего значения функции. 3) воспитывать аккуратность выполнения записей в тетради и на доске. 4) способствовать развитию внимания
Задачи урока
Обучающая: отработка умений нахождения наибольшего и наименьшего значений функции на отрезке.
Развивающая: развитие познавательного интереса через решение задач, логического мышления.
Воспитательная: создание условий для формирования самооценки знаний, творческой активности, преодоления трудностей.
Оборудование: компьютер, проектор, карточки с индивидуальными заданиями
Слайд 4Задание 1. Найдите производную функции:
Ход урока:
Организационный момент.
Устная работа (для всего
класса с помощью проектора предлагается разминка)
Слайд 6Задание 3 .Найдите промежутки возрастания и убывания функции:
Решение:
0,3
+
-
функция убывает
функция возрастает
Слайд 7Задание 3 .Найдите промежутки возрастания и убывания функции:
Решение:
+
-
-6
функция убывает
функция возрастает
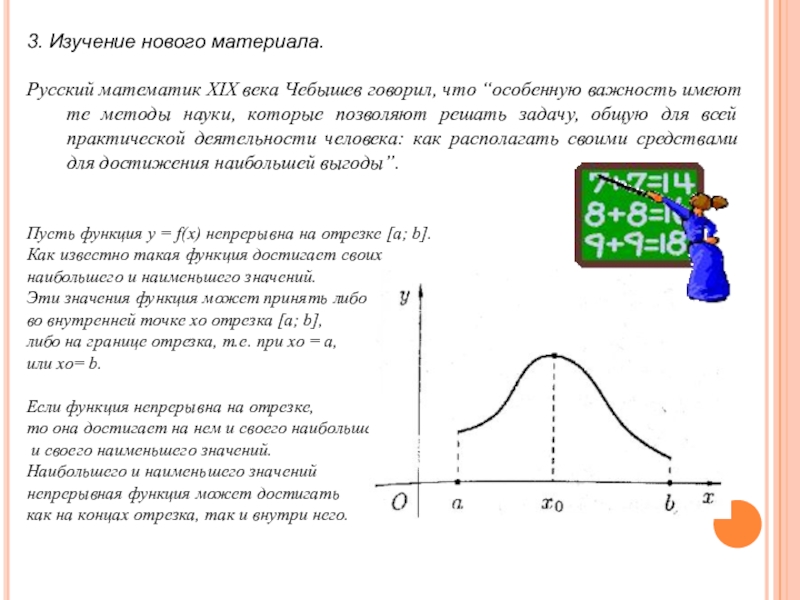
Слайд 93. Изучение нового материала.
Русский математик XIX века Чебышев говорил, что
“особенную важность имеют те методы науки, которые позволяют решать задачу,
общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды”.Пусть функция у = f(х) непрерывна на отрезке [а; b].
Как известно такая функция достигает своих
наибольшего и наименьшего значений.
Эти значения функция может принять либо
во внутренней точке xo отрезка [а; b],
либо на границе отрезка, т.е. при xo = а,
или xo= b.
Если функция непрерывна на отрезке,
то она достигает на нем и своего наибольшего
и своего наименьшего значений.
Наибольшего и наименьшего значений
непрерывная функция может достигать
как на концах отрезка, так и внутри него.
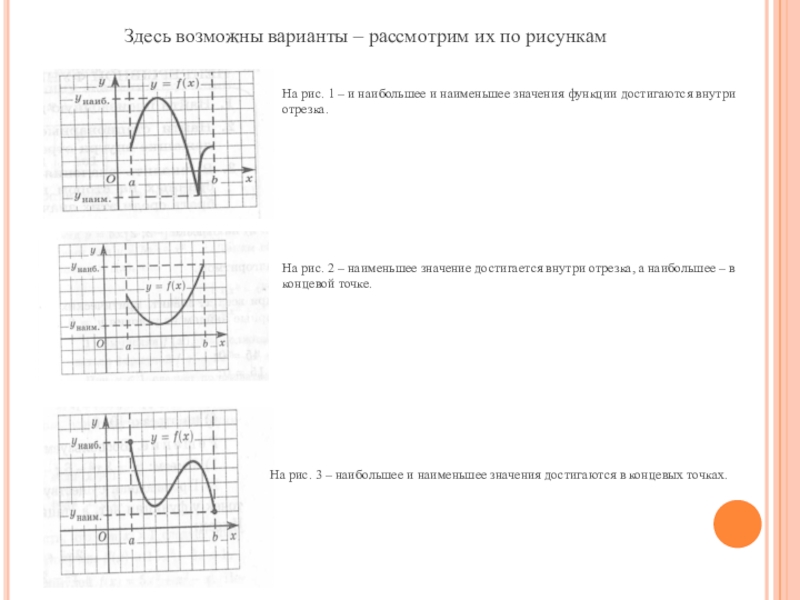
Слайд 10Здесь возможны варианты – рассмотрим их по рисункам
На рис.
1 – и наибольшее и наименьшее значения функции достигаются внутри
отрезка.На рис. 2 – наименьшее значение достигается внутри отрезка, а наибольшее – в концевой точке.
На рис. 3 – наибольшее и наименьшее значения достигаются в концевых точках.
Слайд 11Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции y=f(x) на
отрезке [а;b]
Найти производную f ‘(x).
Найти стационарные и критические точки функции,
лежащие внутри отрезка [a;b].Вычислить значения функции в точках, отобранных на втором шаге (п. 2), и в точках a и b; выбрать среди этих значений наименьшее – это будет y наим. и наибольшее – это будет y наиб.
Слайд 12 4. Закрепление нового материала.
Найдите наименьшее и наибольшее значения
функции:
а) у = х4 – 2х3 – 3 на [0;
2];б) у = 2х2 – 4х + 3 на [0; 4];
в) у = 3х2 – х3 на [-1; 3]
Слайд 13
4. Подведение итога урока. Выставление оценок.
Чем сегодня мы
занимались на уроке?
Как звучит алгоритм нахождения наибольшего и
наименьшего значений функции на отрезке?Соответствует ли урок поставленным целям?
Оцените свои результаты.
5. Домашнее задание.








![Отыскание наибольшего и наименьшего значений непрерывной функции Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [а;b]Найти производную f ‘(x).Найти стационарные и](/img/thumbs/a1bb16152a4a7f76859b7af070c5f332-800x.jpg)






















