Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПИРАМИДА
Содержание
- 1. ПИРАМИДА
- 2. Пирамида – многогранник, основание которого – многоугольник,
- 3. ПирамидыТреугольная пирамида (тетраэдр)Шестиугольная пирамидаЧетырехугольная пирамида
- 4. Элементы пирамидыбоковые грани — треугольники, сходящиеся в
- 5. Элементы пирамиды боковые грани — треугольники, сходящиеся
- 6. Элементы пирамидывысота — перпендикуляр, проведённый через вершину
- 7. Правильная пирамидаПирамида называется правильной, если ее основание
- 8. Все апофемы правильной пирамиды равны друг другуПравильная
- 9. Усеченная пирамида - это многогранник, образованный пирамидой
- 10. - это многогранник, образованный пирамидой и
- 11. Все боковые грани усеченной пирамиды - трапецииУсеченная
- 12. Усеченная пирамида называется правильной, если она получена
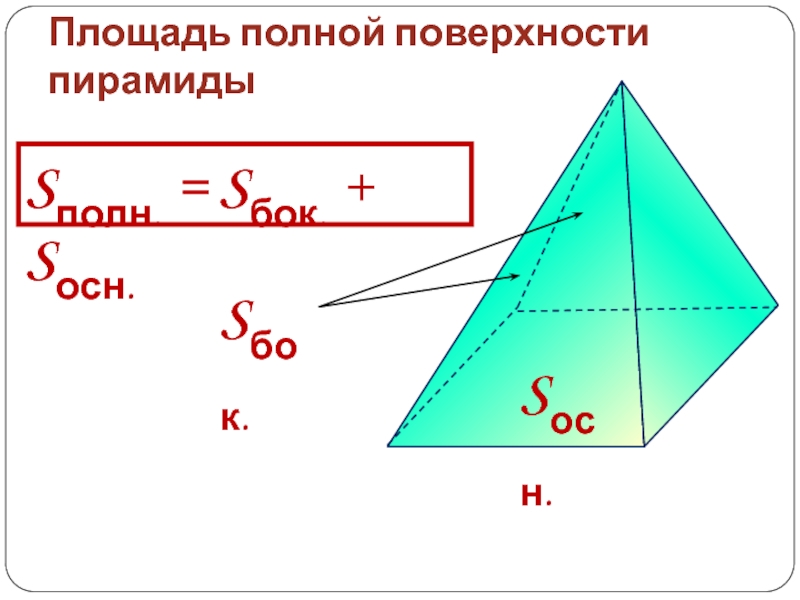
- 13. Площадь полной поверхности пирамидыSполн. = Sбок. + Sосн. Sбок.Sосн.
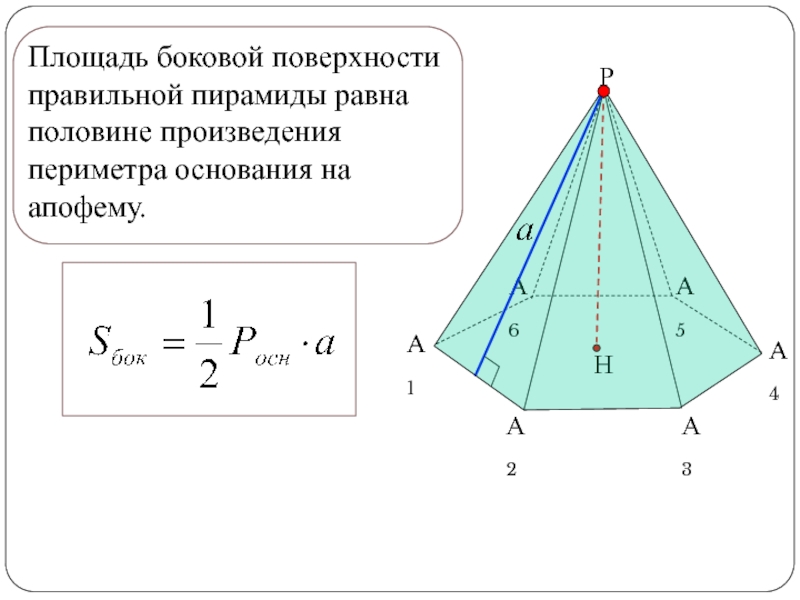
- 14. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
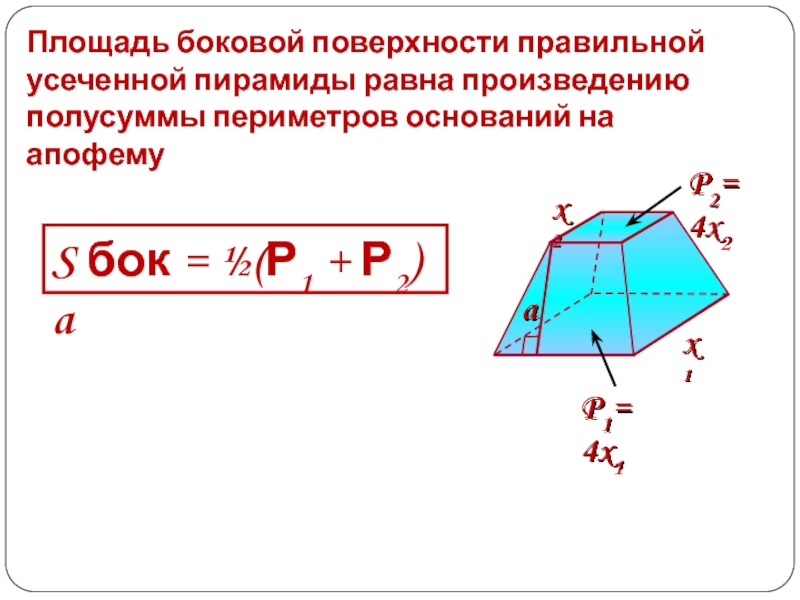
- 15. Площадь боковой поверхности правильной усеченной пирамиды равна
- 16. ПЛОЩАДЬ ПОВЕРХНОСТИ ПИРАМИДЫПлощадь полной поверхности
- 17. Правильная пирамида
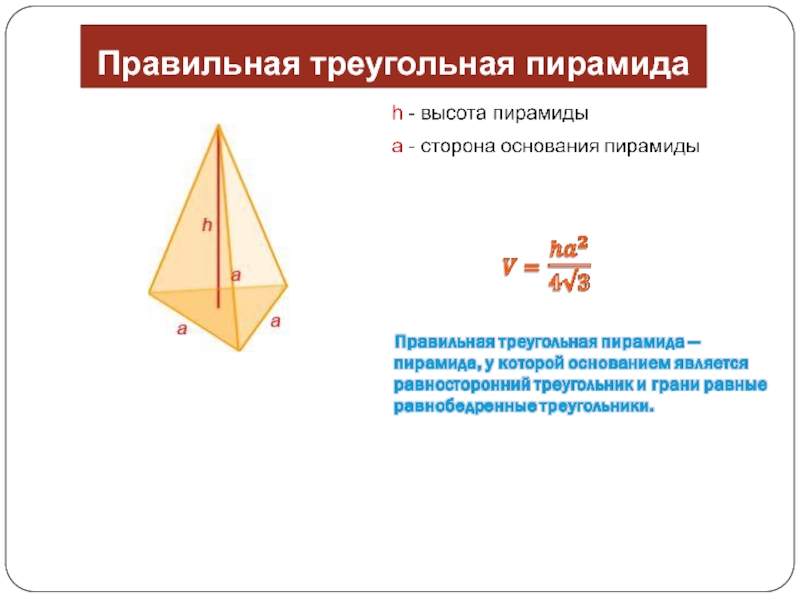
- 18. Правильная треугольная пирамида
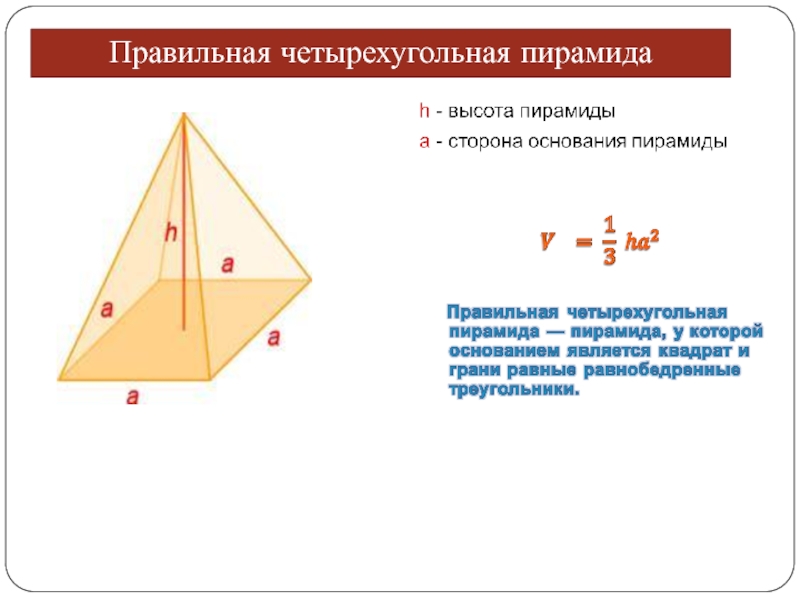
- 19. Правильная четырехугольная пирамида
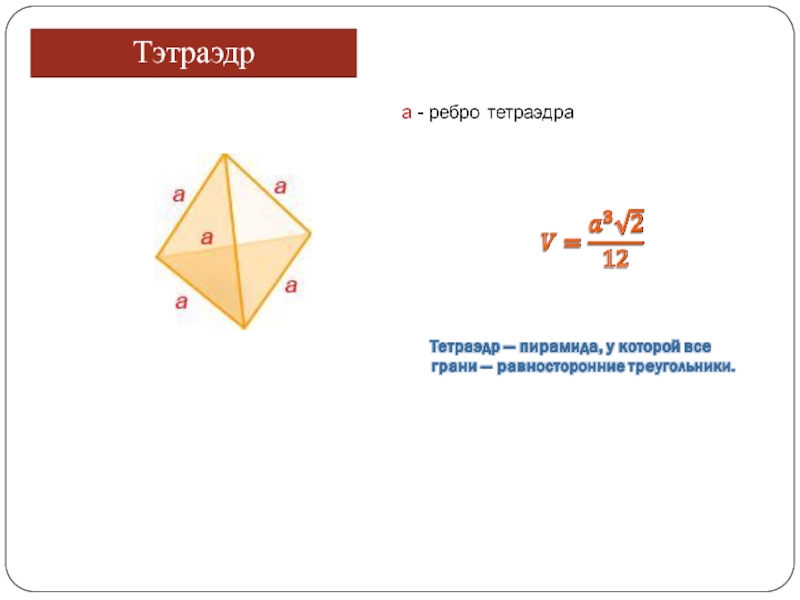
- 20. Тэтраэдр
- 21. Формулы площади и объема ПИРАМИДЫ:1) Площадь боковой поверхности правильной пирамиды2) Площадь боковой поверхности правильной усеченной пирамиды
- 22. 3) Площадь полной поверхности пирамиды4) Площадь полной поверхности усеченной пирамидыФормулы площади и объема ПИРАМИДЫ:5) Объем пирамиды
- 23. 8) Объем усеченной пирамидыФОРМУЛЫ ПЛОЩАДИ И ОБЪЕМА ПИРАМИДЫ:6) Объем правильной треугольной пирамиды7) Объем правильной четырехугольной пирамиды
- 24. 9) Объем и площадь полной поверхности правильного
- 25. В правильной четырехугольной пирамиде апофема равна
- 26. 2. В правильной четырехугольной пирамиде площадь боковой
- 27. 3. В правильной треугольной пирамиде апофема, равная
- 28. 4. В правильной четырехугольной усеченной пирамиде площади
- 29. Слайд 29
- 30. Слайд 30
- 31. Скачать презентанцию
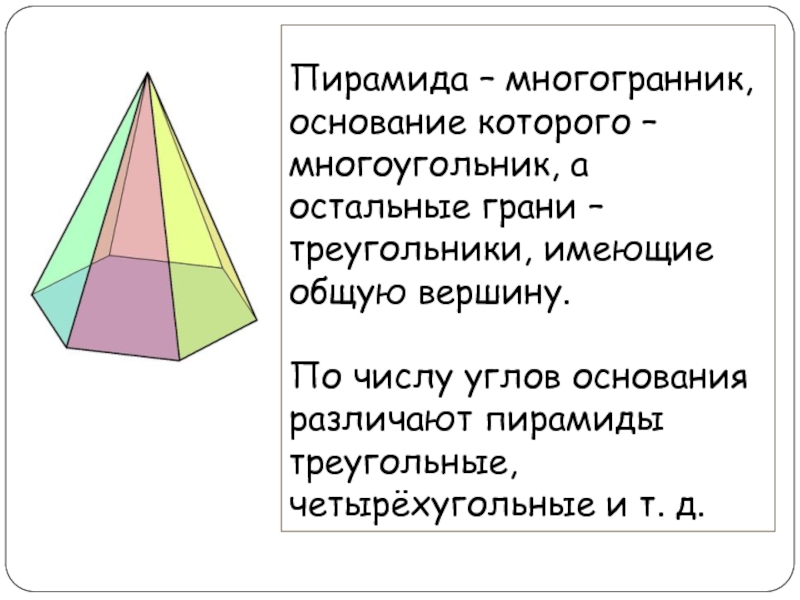
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.
Слайды и текст этой презентации
Слайд 4
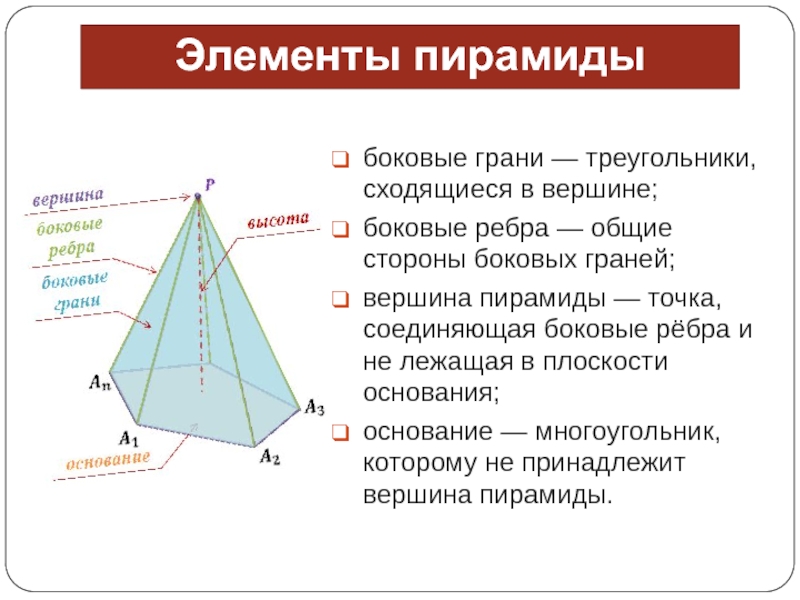
Элементы пирамиды
боковые грани — треугольники, сходящиеся в вершине;
боковые ребра — общие стороны
боковых граней;
вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая
в плоскости основания;основание — многоугольник, которому не принадлежит вершина пирамиды;
высота — перпендикуляр, проведённый через вершину пирамиды к плоскости её основания;
диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
Слайд 5
Элементы пирамиды
боковые грани — треугольники, сходящиеся в вершине;
боковые ребра — общие стороны
боковых граней;
вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая
в плоскости основания;основание — многоугольник, которому не принадлежит вершина пирамиды.
Слайд 6
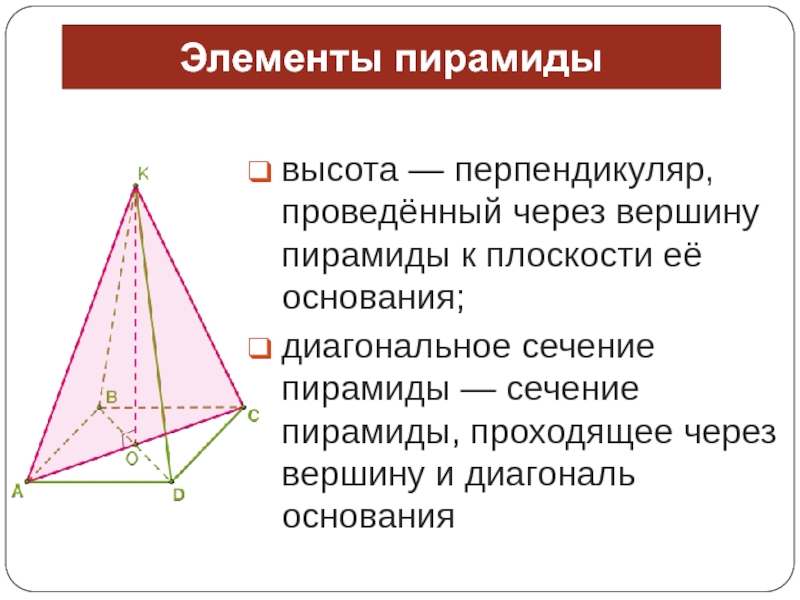
Элементы пирамиды
высота — перпендикуляр, проведённый через вершину пирамиды к плоскости её
основания;
диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ
основанияСлайд 7Правильная пирамида
Пирамида называется правильной, если ее основание – правильный многоугольник
и высота проходит через центр основания.
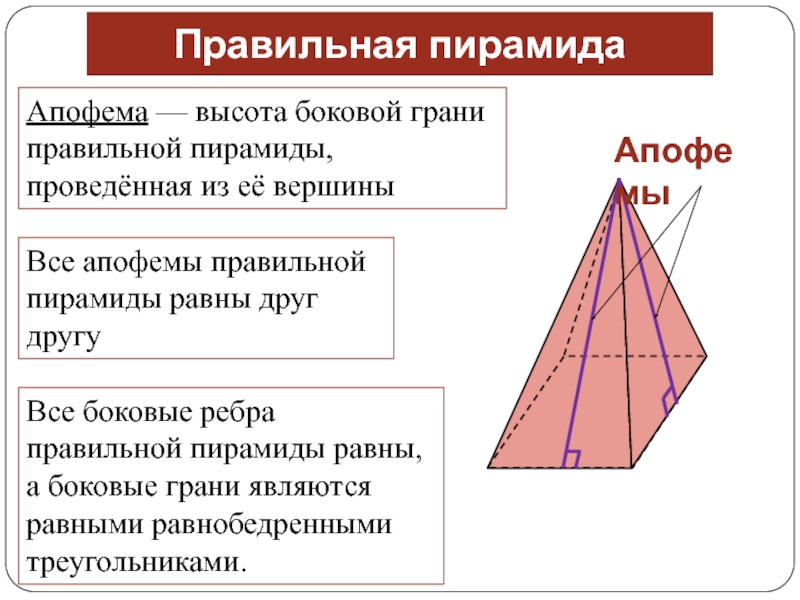
Слайд 8Все апофемы правильной пирамиды равны друг другу
Правильная пирамида
Все боковые ребра
правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Апофема —
высота боковой грани правильной пирамиды, проведённая из её вершиныСлайд 9
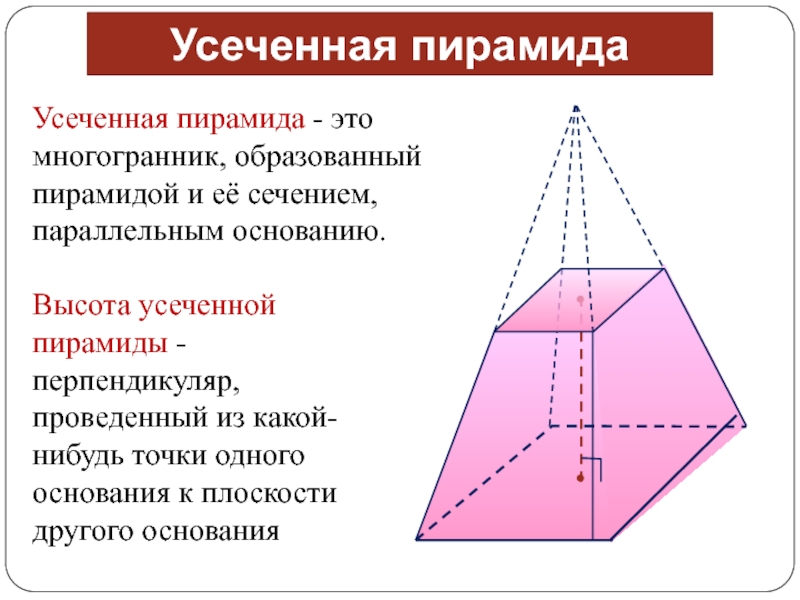
Усеченная пирамида - это многогранник, образованный пирамидой и её сечением,
параллельным основанию.
Усеченная пирамида
Высота усеченной пирамиды - перпендикуляр, проведенный из
какой-нибудь точки одного основания к плоскости другого основанияСлайд 10
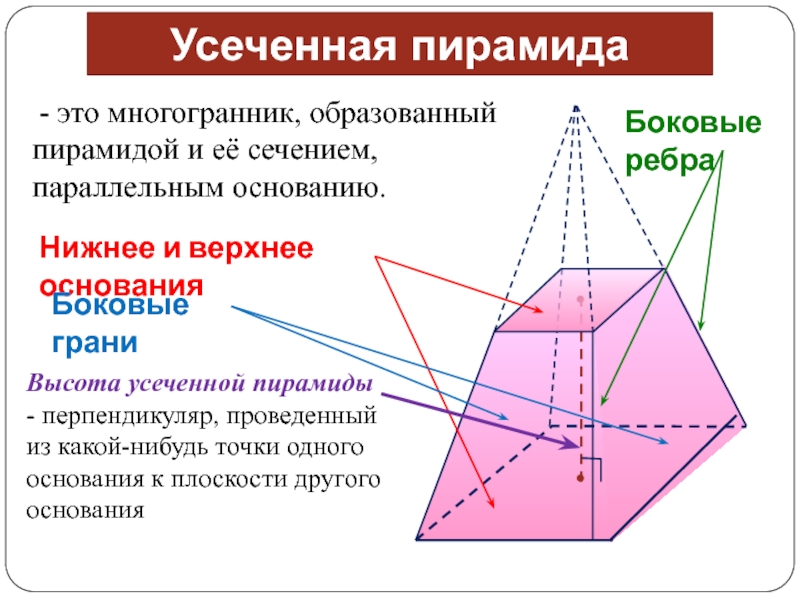
- это многогранник, образованный пирамидой и её сечением, параллельным
основанию.
Нижнее и верхнее основания
Боковые грани
Боковые ребра
Усеченная пирамида
Высота усеченной пирамиды
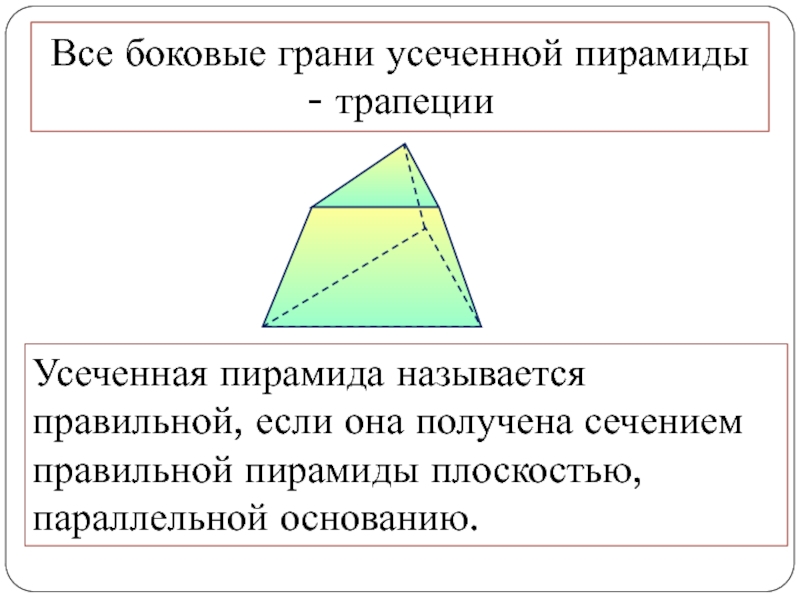
- перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основанияСлайд 11Все боковые грани усеченной пирамиды - трапеции
Усеченная пирамида называется правильной,
если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
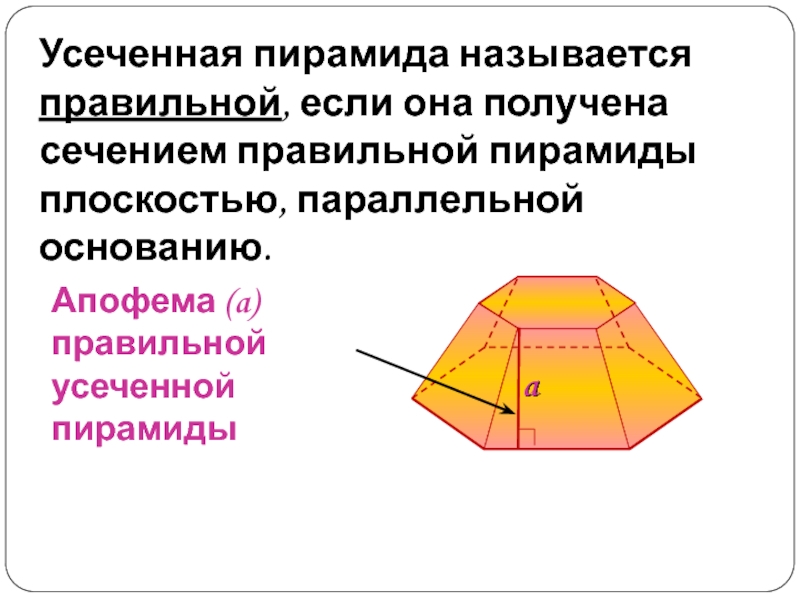
Слайд 12Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды
плоскостью, параллельной основанию.
Апофема (a) правильной усеченной пирамиды
Слайд 14
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания
на апофему.
Слайд 15Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров
оснований на апофему
S бок = ½(Р1 + Р2) a
Слайд 16ПЛОЩАДЬ ПОВЕРХНОСТИ ПИРАМИДЫ
Площадь полной поверхности
Площадь боковой поверхности
правильной пирамиды
Площадь боковой поверхности правильной усеченной пирамиды
Слайд 21Формулы площади и объема ПИРАМИДЫ:
1) Площадь боковой поверхности правильной пирамиды
2)
Площадь боковой поверхности правильной усеченной пирамиды
Слайд 223) Площадь полной поверхности пирамиды
4) Площадь полной поверхности усеченной пирамиды
Формулы
площади и объема ПИРАМИДЫ:
5) Объем пирамиды
Слайд 238) Объем усеченной пирамиды
ФОРМУЛЫ ПЛОЩАДИ И ОБЪЕМА ПИРАМИДЫ:
6) Объем правильной
треугольной пирамиды
7) Объем правильной четырехугольной пирамиды
Слайд 249) Объем и площадь полной поверхности правильного тетраэдра
ФОРМУЛЫ ПЛОЩАДИ И
ОБЪЕМА ПИРАМИДЫ:
10) Объем правильной n-угольной пирамиды
Слайд 25 В правильной четырехугольной пирамиде апофема равна 17см, высота 15см.
Найти объем, площадь боковой и полной поверхности пирамиды.
Решение задач на
пирамидуСлайд 262. В правильной четырехугольной пирамиде площадь боковой поверхности равна 240
см², а площадь полной поверхности – 384 см². Найдите сторону
основания x и высоту h пирамиды. Вычислить объем пирамиды.Решение задач на пирамиду
Слайд 273. В правильной треугольной пирамиде апофема, равная 6 см, составляет
с плоскостью основания угол 60°. Вычислите площадь полной поверхности пирамиды.
Решение
задач на пирамидуСлайд 284. В правильной четырехугольной усеченной пирамиде площади оснований равны 25
см² и 9 см², а боковое ребро образует с плоскостью
нижнего основания угол 45°. Вычислите площадь боковой поверхности пирамиды.Решение задач на пирамиду