Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к ЕГЭ по математике по теме "Производная"
Содержание
- 1. Подготовка к ЕГЭ по математике по теме "Производная"
- 2. Подготовка к ЕГЭ по математикеПрототипы задания B8
- 3. Цель урока: обобщение и систематизация решения
- 4. Геометрический смысл производнойЗначение производной функции
- 5. Задача. На рисунке дан график функции y=f(x),
- 6. Если f’(x) > 0 на промежутке, то
- 7. Задача. На рисунке изображен график функции y
- 8. Задача. На рисунке изображен график функции у
- 9. Если прямые параллельны, то их угловыекоэффициенты равныf’(x₀)
- 10. Слайд 10
- 11. Точка хo называется точкой максимума функции f(х),
- 12. Точки минимума и точки максимума называются точками
- 13. Задача. На рисунке изображен график производной функции
- 14. Диагностическая работа
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
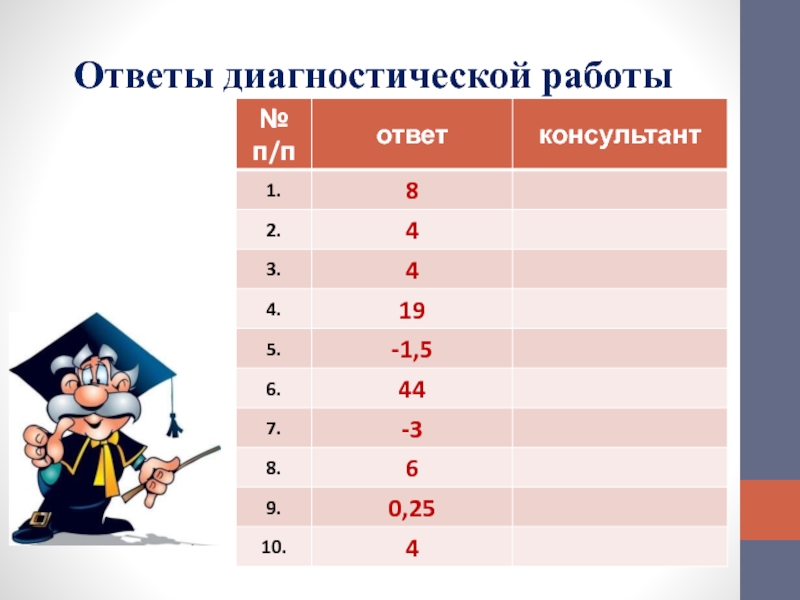
- 19. Ответы диагностической работы
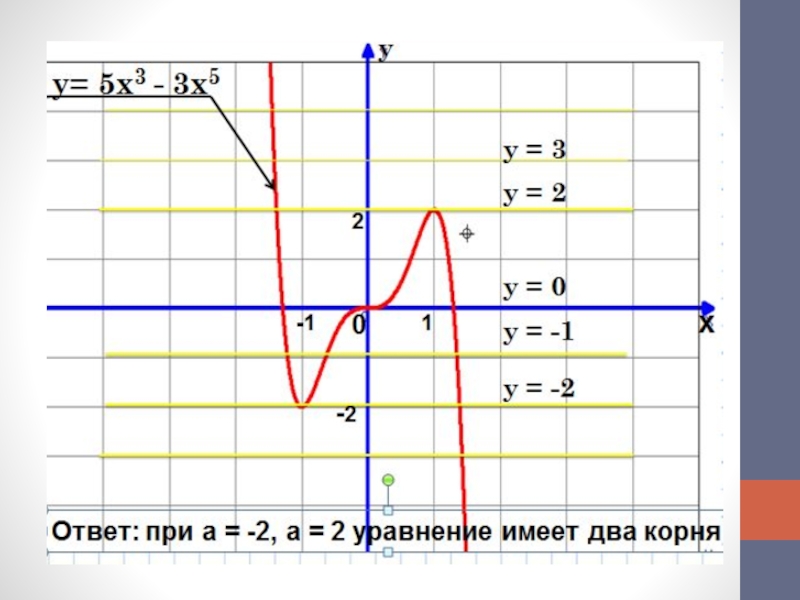
- 20. Задача С 5 (ЕГЭ)
- 21. Слайд 21
- 22. Одиннадцать лет ты за партой сидел,Старался, учился,
- 23. Скачать презентанцию
Подготовка к ЕГЭ по математикеПрототипы задания B8
Слайды и текст этой презентации
Слайд 3Цель урока: обобщение и систематизация решения прототипов
задания В8 на ЕГЭ по математике.
Задачи:
повторить теоретический материал прототипов заданий
В8;формировать умения самостоятельно и мотивированно организовывать свою деятельность;
развивать творческие способности применения знаний и умений в решении вариантов ЕГЭ по математике.
Слайд 4 Геометрический смысл производной
Значение производной функции в точке равно
угловому коэффициенту касательной к графику функции в этой точке (тангенсу
угла между касательной и осью Ох).f’(хo) = k = tg α
α – это угол между касательной и положительным направлением оси Ох
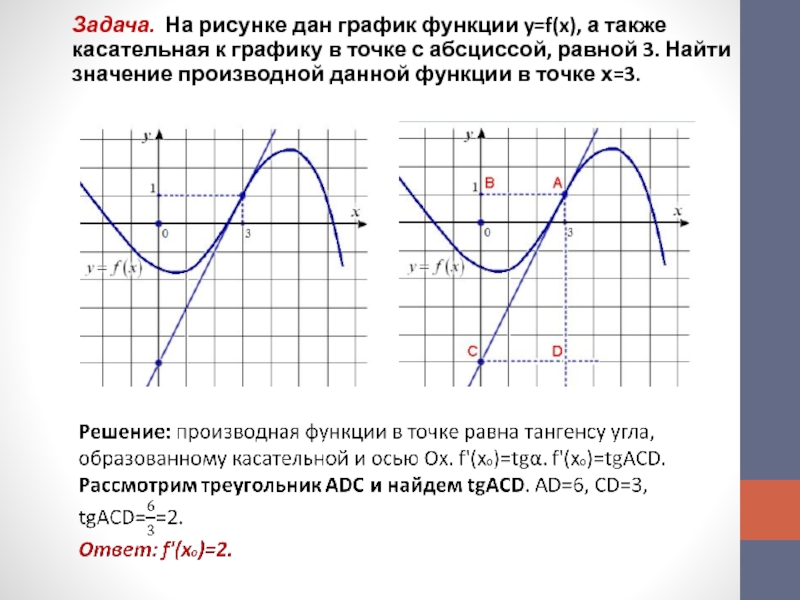
Слайд 5Задача. На рисунке дан график функции y=f(x), а также касательная
к графику в точке с абсциссой, равной 3. Найти значение
производной данной функции в точке х=3.Слайд 6Если f’(x) > 0 на промежутке, то функция f(x) возрастает
на этом промежутке.
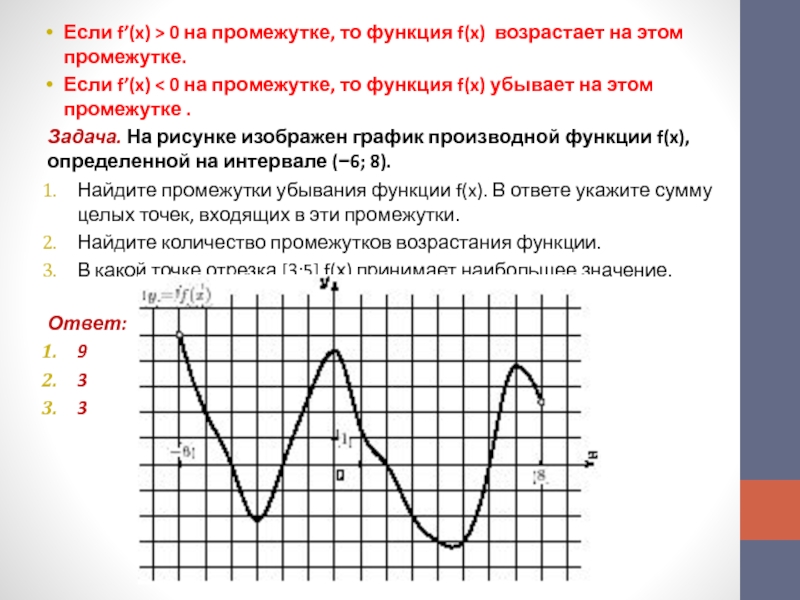
Если f’(x) < 0 на промежутке, то функция
f(x) убывает на этом промежутке .Задача. На рисунке изображен график производной функции f(x), определенной на интервале (−6; 8).
Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Найдите количество промежутков возрастания функции.
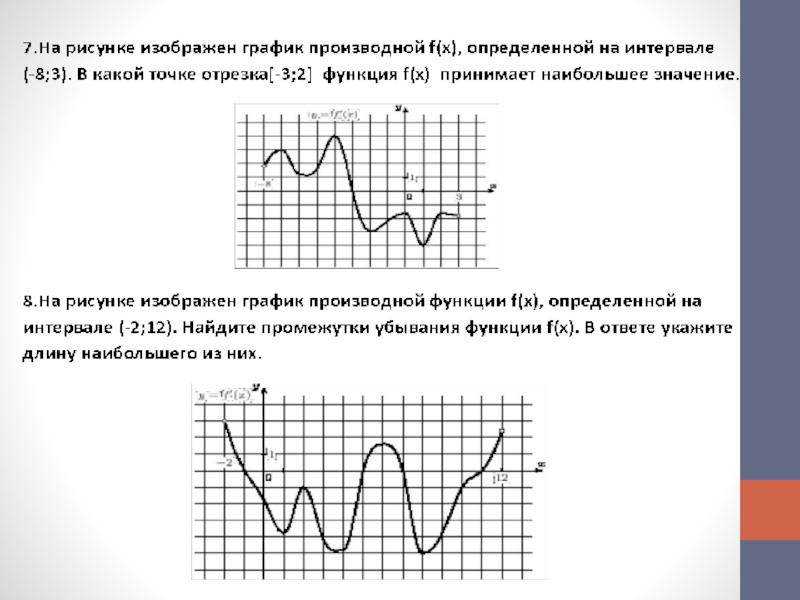
В какой точке отрезка [3;5] f(х) принимает наибольшее значение.
Ответ:
9
3
3
Слайд 7Задача. На рисунке изображен график функции y = f(x),
определенной
на интервале (-6; 5). Найдите количество точек, в которых производная
функции f(x) равна 0.Ответ: 6
Слайд 8Задача. На рисунке изображен график функции у = f(x),
определенной на интервале (-7; 5). Найдите количество точек,
в
которых касательная к графику функции параллельна прямой у = -15.
Ответ: 5
Слайд 9Если прямые параллельны, то их угловые
коэффициенты равны
f’(x₀) = k =
tgα
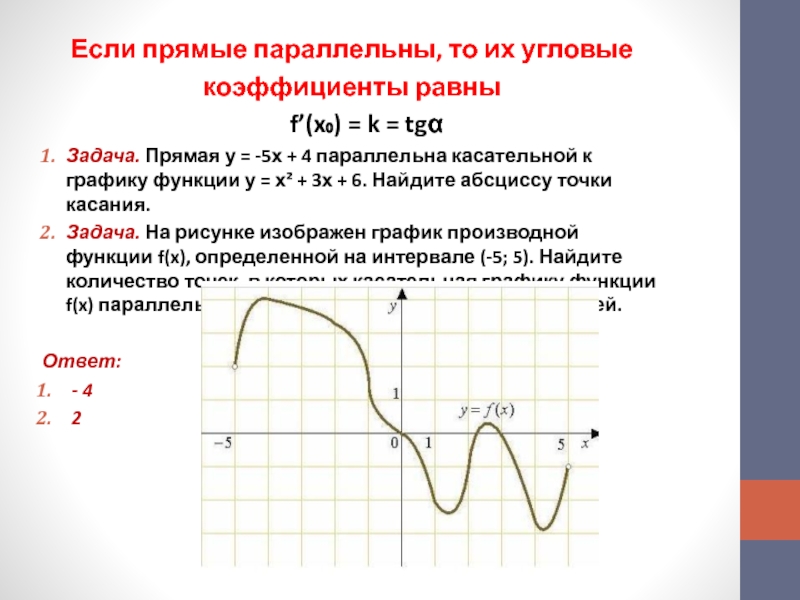
Задача. Прямая у = -5х + 4 параллельна касательной к
графику функции у = х² + 3х + 6. Найдите абсциссу точки касания.Задача. На рисунке изображен график производной функции f(x), определенной на интервале (-5; 5). Найдите количество точек, в которых касательная графику функции f(x) параллельна прямой у = 3х – 8 или совпадает с ней.
Ответ:
- 4
2
Слайд 11Точка хo называется точкой максимума функции f(х), если
существует такая окрестность точки хo, что для всех х≠ хo
из этой окресности выполняется неравенство f(х) < f(хo).
Точка хo называется точкой минимума функции f(х),
если существует такая окрестность точки хo, что для всех х≠ хo
из этой окрестности выполняется неравенство f(х) > f(хo) = 0.
Если хo – точка экстремума дифференцируемой функции f(х),
то f’(хo) = 0.
Пусть функция f(х) дифференцируема на интервале (a; b), хo Є (a; b),
и f’(хo) = 0:
Если при переходе через стационарную точку хo функции f(х) ее производная меняет знак с «плюса» на «минус», т. е. f’(х) > 0 слева от точки хo и f’(х) < 0 справа от точки хo, то хo – точка максимума функции f(х);
Если при переходе через стационарную точку хo функции f(х) ее производная меняет знак с «минуса» на «плюс», то хo – точка минимума функции f(х).
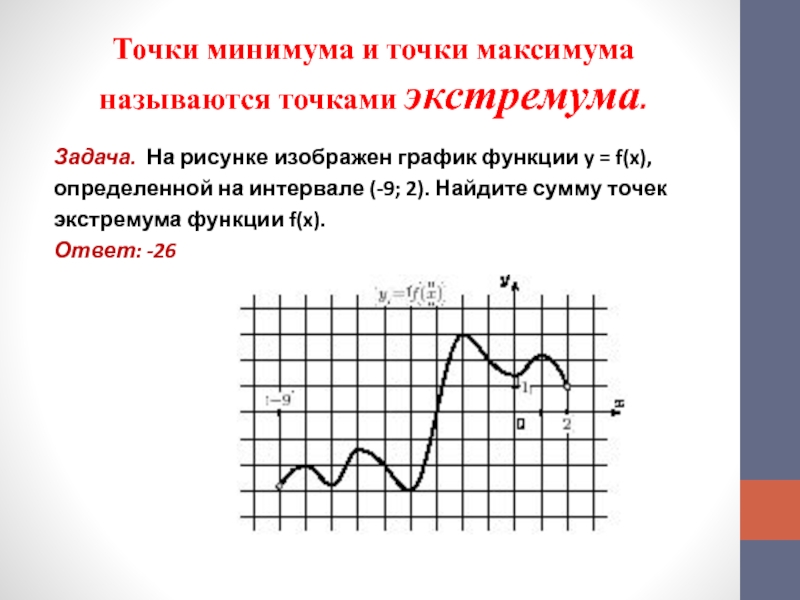
Слайд 12Точки минимума и точки максимума называются точками экстремума.
Задача. На рисунке
изображен график функции y = f(x),
определенной на интервале (-9;
2). Найдите сумму точек экстремума функции f(x).
Ответ: -26
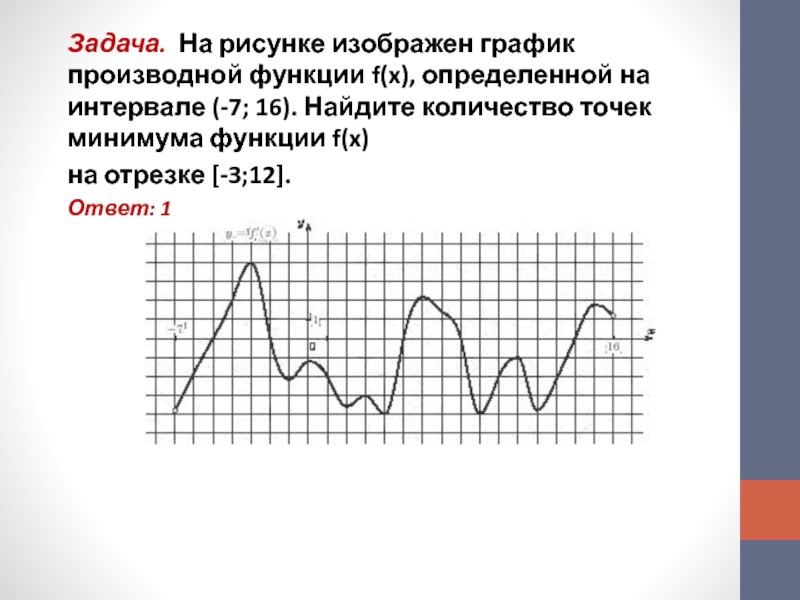
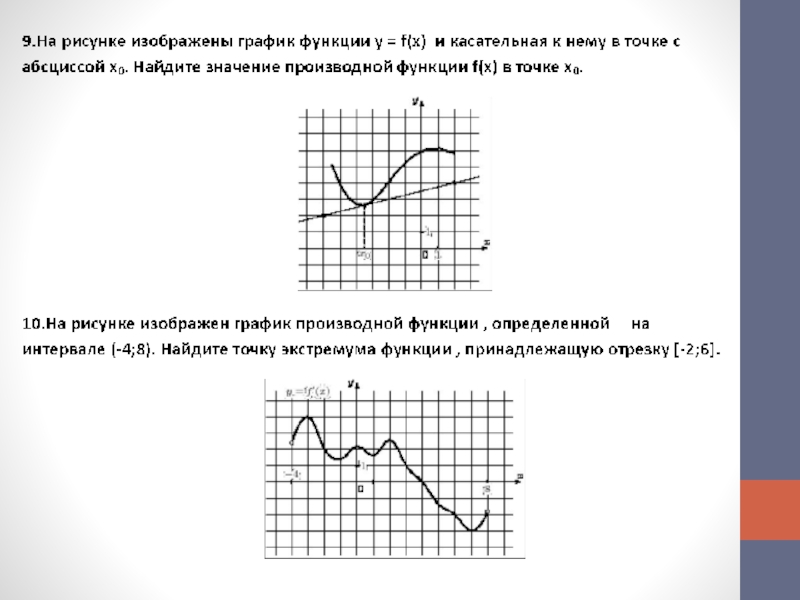
Слайд 13Задача. На рисунке изображен график производной функции f(x), определенной на
интервале (-7; 16). Найдите количество точек минимума функции f(x)
на
отрезке [-3;12]. Ответ: 1




 0 на промежутке, то функция f(x) возрастает на" alt="Если f’(x) > 0 на промежутке, то функция f(x) возрастает на этом промежутке.Если f’(x) < 0 на">
0 на промежутке, то функция f(x) возрастает на" alt="Если f’(x) > 0 на промежутке, то функция f(x) возрастает на этом промежутке.Если f’(x) < 0 на">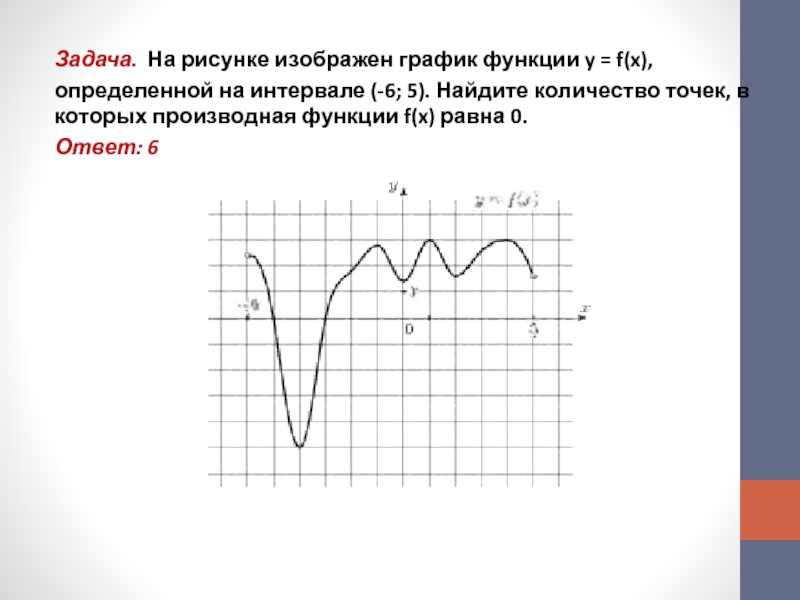
























![Сложение и вычитание вида []+4, []-4](/img/thumbs/605739bbda80b8f279b676f7db1e2062-800x.jpg)
