Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показательная функция, её свойства и график
Содержание
- 1. Показательная функция, её свойства и график
- 2. Цель и задачи урока
- 3. Степень с иррациональным показателемr =
- 4. Определение показательной функции Функция вида y
- 5. Основные свойства степени
- 6. Основные свойства степени6) Если m > n,
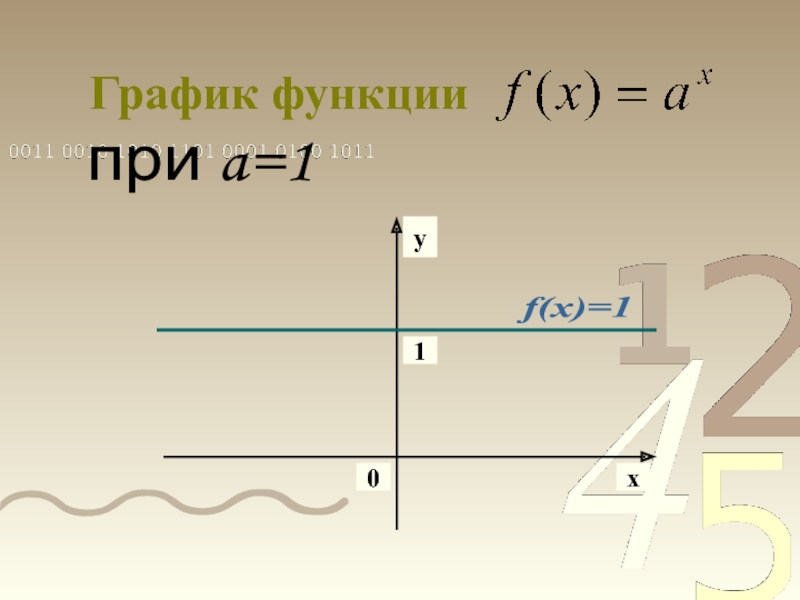
- 7. График функциипри a=1уx01f(x)=1
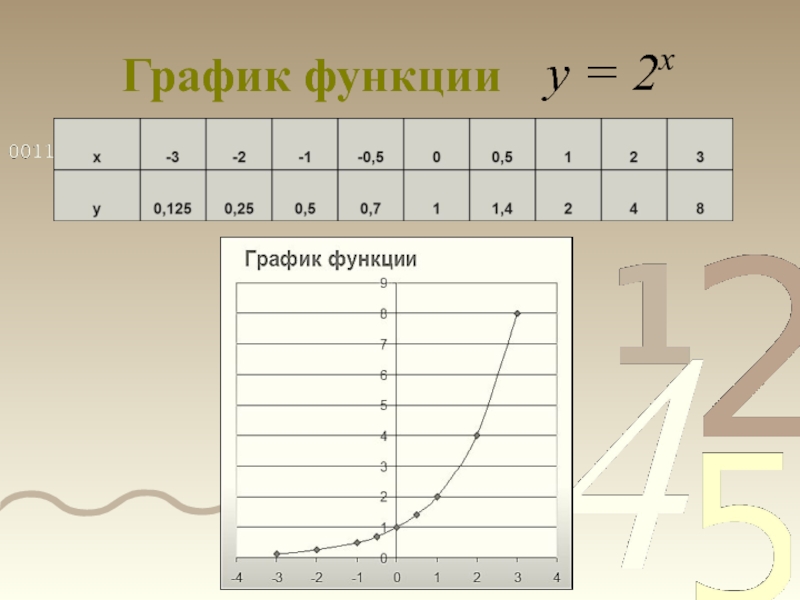
- 8. График функции y = 2x
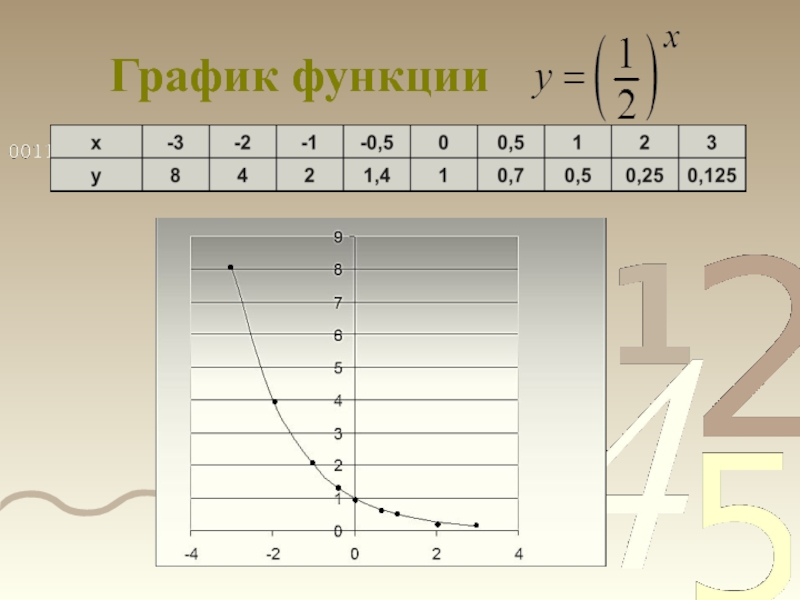
- 9. График функции
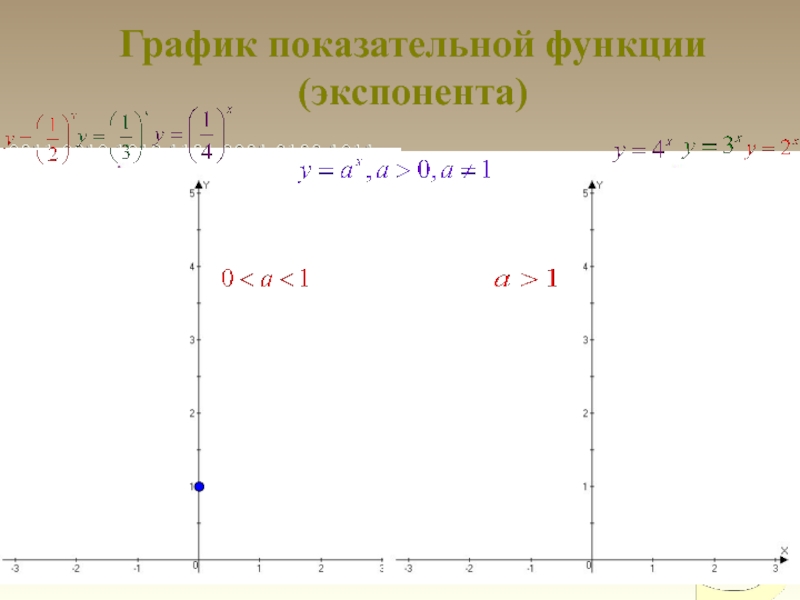
- 10. График показательной функции (экспонента)
- 11. Свойства функции
- 12. Свойства показательной функцииyx1о1) Область определения –
- 13. Выберите возрастающую функцию:
- 14. Выберите убывающую функцию:
- 15. Укажите область значений функции
- 16. Подведём итогОпределениеГрафикСвойстваПримененияПоказательная функцияПоказательная функция
- 17. Скачать презентанцию
Цель и задачи урока
Слайды и текст этой презентации
Слайд 3Степень с иррациональным показателем
r = = 1,414213…
rn
= 1; 1,4; 1,41; 1,414; 1,4142; 1,41421…
r'n = 2;
1,5; 1,42; 1,4115; 1,4143; 1,41422…3 < 3 < 3
Слайд 4Определение показательной функции
Функция вида y = ax
называется
показательной с основанием а.
Замечание.
Вместе с функцией y=ax показательной считают
и функцию вида y=Cax, где С- некоторая постоянная.Слайд 11Свойства функции
Проанализируем по схеме:
1. область определения функции
2. множество значений функции
3. нули функции4. промежутки знакопостоянства функции
5. четность или нечётность функции
6. монотонность функции
7. наибольшее и наименьшее значения
8. периодичность функции
9. ограниченность функции
Слайд 12Свойства показательной функции
y
x
1
о
1) Область определения –
множество всех
действительных чисел (D(у)=R).
2) Множество значений – множество всех
положительных чисел (E(y)=R+).
3) Нулей нет.
4) у>0 при х ϵ R.
5) Функция ни чётная, ни нечётная.
6) Функция монотонна: возрастает на R при а>1
и убывает на R при 0
8) Функция непериодична.
9) Ограничена снизу, не ограничена сверху.