Слайд 1
Министерство образования, науки и молодежи Республики Крым
Государственное бюджетное образовательное учреждение
дополнительного образования Республики Крым «Малая академия наук «Искатель»
«ГРАФИКИ ФУНКЦИЙ,
СОДЕРЖАЩИХ
ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ»
Работу выполнила :
Юдина Анастасияи Олеговна
обучающейся 9-А класса
МБОУ «СОШ №1
им. Маргелова В.Ф.»
г.Красноперекопск
Руководитель:
Коробова Елена Анатольевна
учитель математики
МБОУ «СОШ №1
им. Маргелова В.Ф.»
г.Красноперекопск
Красноперекопск 2018
Слайд 2Цель моей исследовательской работы:
1. Провести исследование и анализ имеющихся
способов построения графиков функций, содержащих переменную под знаком модуля .
2.
Выбрать из найденных способов решения наиболее оптимальные.
3. Провести обобщение и систематизацию имеющего материала:
а) научиться строить графики функций, содержащих переменную под знаком модуля;
б) составить подборку задач по теме "Графики функций, содержащих переменную под знаком модуля".
Слайд 3
ВВЕДЕНИЕ
Понятие «модуль» широко применяется во многих разделах
школьного курса математики, например, в изучении абсолютной и относительной погрешностей
приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках.
Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.
Слайд 4 Задача исследования:
1) используя различные методы исследования (теоретический, практический, исследовательский),
углубить знания по теории модуля и научиться решать задачи, выходящие
за страницы школьных учебников, тем самым расширить познавательный интерес к изучению алгебры;
2) на примере задач посмотреть, можно ли знания по теме "Графики функций, содержащие модуль", использовать для решения задач из реальной жизни.
Объект исследования: Плоскость и поведение на ней различных функциональных зависимостей.
Предмет исследования: Механизм построения графиков кусочно-линейных и кусочно-квадратичных функций определённых на множестве действительных чисел.
Слайд 52. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ, СОДЕРЖАЩИХ МОДУЛИ
Для построения всех типов графиков необходимо понимать определение
модуля и знать виды простейших графиков, изучаемых в школе.
Целесообразно рассматривать построение графиков в следующей последовательности:
у=f(∣x∣); у=∣f(x)∣; у=∣f(∣x∣)∣; у=∣f(x)∣ + ∣g(x)∣ + ...; ∣у∣=f(x); ∣у∣=∣f(x)∣.
Построение графиков следует осуществлять двумя способами:
1) на основании определения модуля;
2) на основании правил (алгоритмов) геометрического преобразования графиков функций.
Слайд 62.1. Построение графика функции у=f(∣x∣)
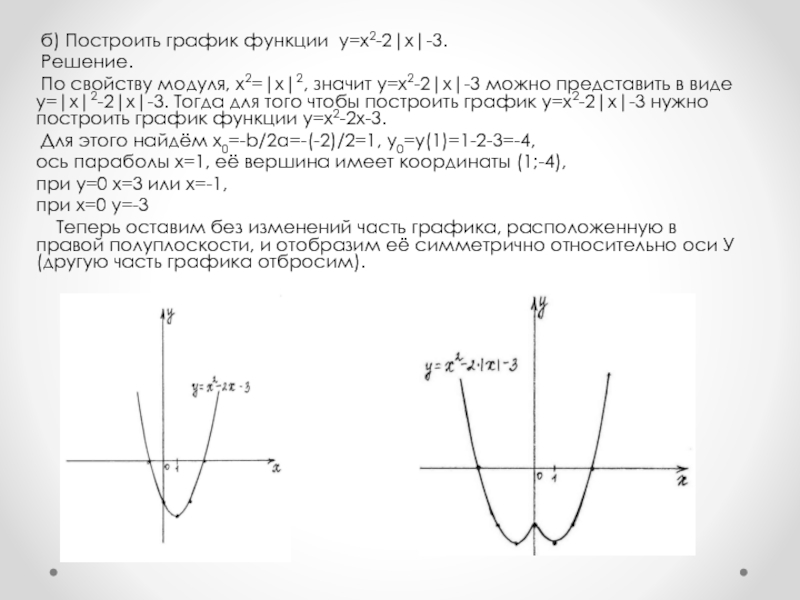
Слайд 7 б) Построить график функции у=х2-2|х|-3.
Решение.
По свойству
модуля, х2=|х|2, значит у=х2-2|х|-3 можно представить в виде у=|х|2-2|х|-3. Тогда
для того чтобы построить график у=х2-2|х|-3 нужно построить график функции у=х2-2х-3.
Для этого найдём х0=-b/2a=-(-2)/2=1, y0=y(1)=1-2-3=-4,
ось параболы х=1, её вершина имеет координаты (1;-4),
при у=0 х=3 или х=-1,
при х=0 у=-3
Теперь оставим без изменений часть графика, расположенную в правой полуплоскости, и отобразим её симметрично относительно оси У(другую часть графика отбросим).
Слайд 82.2. Построение графика функции у=∣f(x)∣
Слайд 102.4. Построение графиков функций вида ∣у∣=f(x)
Слайд 12 Метод вершин
Графиком непрерывной кусочно-линейной функции является ломаная с
двумя бесконечными крайними звеньями.
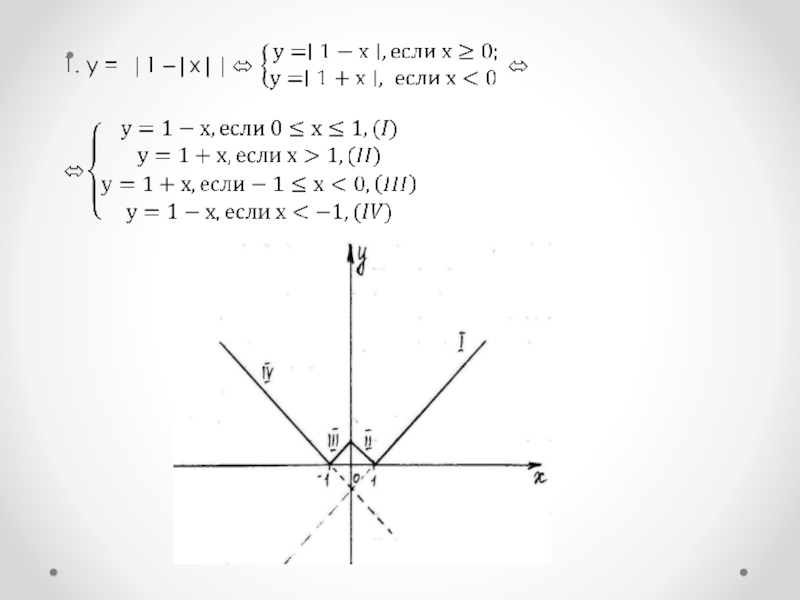
Пример: Построить график функции у=∣х∣-∣х-1∣
Алгоритм построения:
- Найдём
нули каждого подмодульного выражения х=0 и х=1.
- Составим таблицу, в которой кроме 0 и 1 записываем по
одному целому справа и слева от этих значений.
- Наносим эти точки на координатную плоскость и
соединяем последовательно. Точки перелома и есть вершины ломаной
Слайд 134. Решение задач КИМ ГИА по теме "Построение графиков функций,
содержащих переменную под знаком модуля"
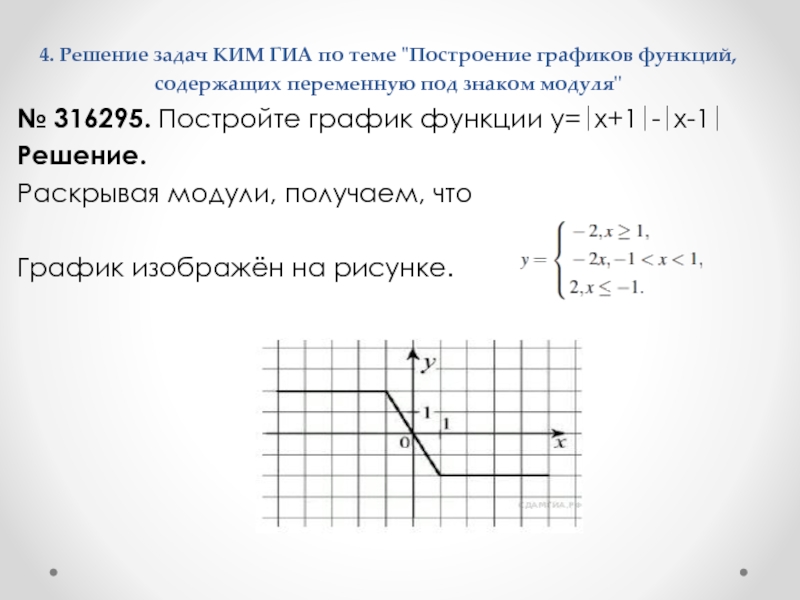
№ 316295. Постройте график функции у=∣х+1∣-∣х-1∣
Решение.
Раскрывая модули, получаем,
что
График изображён на рисунке.
Слайд 145. ЗАКЛЮЧЕНИЕ
В ходе работы мы рассмотрели теоретический материал по абсолютной
величине и решили практические задачи. Многообразие видов таких функций, различия
в построениях их графиков, приобретение новых знаний, сделало нашу работу интересной и увлекательной.
В результате работы над темой я сумела изучить поведения линейных, квадратичных, дробно-рациональных функций. Научилась преобразованию графиков, содержащих знак модуля. Также в ходе выполнения работы я экспериментировала с построением графиков функций, придуманных самостоятельно.
Данная исследовательская работа может быть использована учителями при подготовке к урокам и элективным курсам. Также работа может быть использована учащимися для самоподготовки и самоконтроля при подготовке к экзаменам.
Слайд 15
6.ЛИТЕРАТУРА
1.Гельфанд И. М. и др. « Функции и графики »
- М. Наука, 1973
2. Садыкина И. « Построение графиков
функций и зависимостей, содержащих знак модуля » - Математика №33, 2004
3. Пичурин Л. Ф. « За страницами учебника алгебры » - М. Просвещение, 1999
Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. И. Л. Никольская – М. Просвещение, 1991
4. В.Н.Студенецкая, Л.С.Сагателова "Математика. 8-9 классы: сборник элективных курсов". - Волгоград: Учитель, 2006.
Интернет ресурс
5. Интернет-ресурс:
1) http://www.youtube.com "Построение графиков функций, содержащих модуль". Inna Feldman;
2) http://ppt4web.ru/matematika/postroenie-grafikov-funkcijj-soderzhashhikh-peremennuju-pod-znakom-modulja.html
3) http://www.tutoronline.ru/blog/stroim-grafiki-funkcij,-soderzhawie-modul-chast-1