Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по математике на тему:"Цепные дроби: скрытая красота".
Содержание
- 1. Презентация по математике на тему:"Цепные дроби: скрытая красота".
- 2. Актуальность данной темы состоит в
- 3. Введение В процессе работы я
- 4. Ничто не нравится, кроме красоты, в красоте
- 5. Историческая справкаРафаэль Бомбелли итальянский математик (1526-1572)Христиан Гюйгенснидерландский механик, физик, математик, астроном и изобретатель (1629-1695)Леонард Эйлер швейцарский, немецкий и российский математик и механик(1707-1783).
- 6. ОпределениеЦепная дробь (или непрерывная дробь) — это математическое выражение вида
- 7. Свойства 1. Всякое рациональное
- 8. Реализация алгоритма перевода цепной дроби в действительное
- 9. Реализация алгоритма перевода цепной дроби в действительное
- 10. Реализация алгоритма разложения действительного числа в цепную
- 11. Результаты работы программы1.8 = [1,1,4,0,] 1.6 =
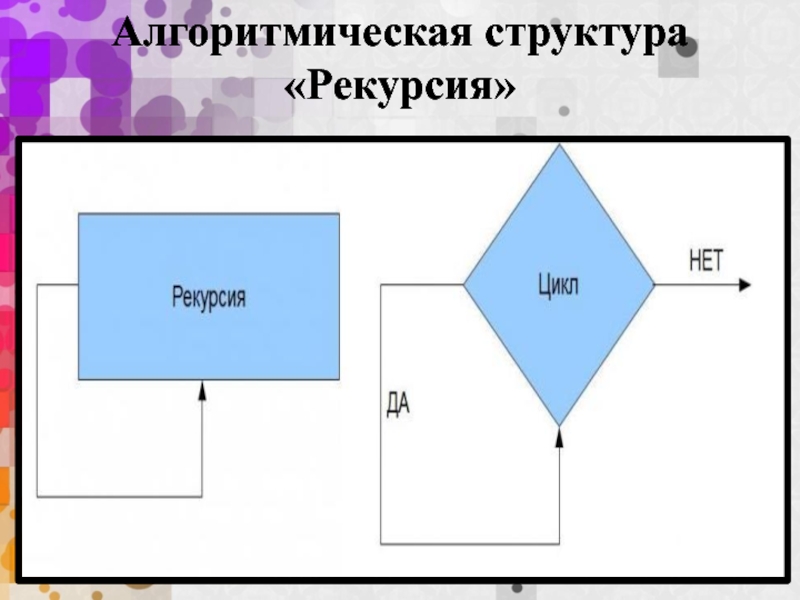
- 12. Алгоритмическая структура «Рекурсия»
- 13. Геометрическое представление цепной дроби
- 14. Бенуа Мандельброт – отец фракталовфранцузский математик, профессор
- 15. Заключение В процессе работы
- 16. Спасибо за внимание!
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПАЛЛАСОВСКИЙ СЕЛЬСКОХОЗЯЙСТВЕННЫЙ ТЕХНИКУМ»
«Цепные дроби: скрытая красота.»
Выполнила:
Сапаргалиева Диана
Албековна студентка группы 1ТВ9
годСлайд 2 Актуальность данной темы состоит в том, что она
интересна своим применением разнообразных задач. Цепные дроби – это вид
действительных чисел. Действительные числа однозначно отображается цепными дробями. Основное значение заключается в том, что зная цепную дробь, изображавшую действительное число, можно определить это число с достаточной точностью. Недостатком цепных дробей является то, что для них никаких практически приемлемых правил арифметических действий не существует. Поэтому широкого применения они не получили.
Объект исследования – дроби.
Предмет исследования – значение цепных дробей.
Цель–изучение истории цепных дробей и применение их при решении заданий.
Задачи:
- изучить историю возникновения цепных дробей;
- исследовать свойства цепных дробей и возможные действия, производимые с ними;
- изучить способы решения заданий с данными дробями;
- найти алгоритмическую структуру, работающую по принципу цепной дроби;
- выяснить возможность геометрического изображения цепных дробей;
- выяснить возможность применения цепных дробей в других науках.
Слайд 3Введение
В процессе работы я пытаюсь раскрыть свойства
подходящих дробей, особенности разложения действительных чисел в неправильные дроби, погрешности,
которые возникают в результате этого разложения, и применение теории цепных дробей для решения ряда алгебраических задач.Цепные дроби были введены в 1572 году итальянским математиком Бом-белли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение. Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.
Слайд 4Ничто не нравится, кроме красоты, в красоте – ничто, кроме
форм, в формах – ничто, кроме пропорций, в пропорциях –
ничто, кроме числа.Аврелий Августин, христианский теолог и философ
Слайд 5Историческая справка
Рафаэль Бомбелли
итальянский математик
(1526-1572)
Христиан Гюйгенс
нидерландский механик, физик, математик,
астроном и
изобретатель
(1629-1695)
Леонард Эйлер
швейцарский,
немецкий и российский
математик и
механик
(1707-1783).
Слайд 7Свойства
1. Всякое рациональное число можно представить
в виде конечной цепной дроби. Числа, входящие в цепную дробь,
называются неполными частными. Иррациональные числа разлагаются в бесконечные цепные дроби. 2. Обрывая цепную дробь, можно получать очень хорошие рациональные приближения к данному числу, которые называются подходящими дробями.
Подходящая дробь – это дробь, которая получается при обрыве бесконечной цепной дроби.
Для числа π = [3; 7, 15, 1, 292, 1, …]
Первые подходящие дроби – это самые известные приближения:
Слайд 8Реализация алгоритма перевода цепной дроби в действительное число
Программа запрашивает
у пользователя знаменатель b и количество вложений n цепной дроби
видаПреобразовывает ее в число и выдает результат в виде десятичной дроби.
Слайд 9Реализация алгоритма перевода цепной дроби в действительное число
Program TO_NUMBER;
var
n, k: integer;
b:real;
begin
write (' введите знаменатель дроби'); read
(b);write (' введите кол-во вложений '); read (n);
for k:=1 to n do b:=1+1/b;
write (' искомое число = ', b); end.
Результаты работы программы
Цепная дробь преобразована в десятичную.
Ошибок не наблюдается.
+ Программа работает корректно.
– Результат представлен в виде десятичной дроби. В случае ее бесконечности компьютер округляет результат.
Слайд 10Реализация алгоритма разложения действительного числа в цепную дробь
Программа просит пользователя
ввести число в виде десятичной дроби. Преобразовав его, выдает результат
видаProgram TO_FRACTION;
var a: array[1..100] of integer;
k, n: integer; x:real;
begin
write (' введите число '); read (x);
k:=1; a[1]:=trunc(x); k:=2;
while frac(x)<>0 do
begin
x:=1/frac(x) ; a[k]:=trunc(x); k:=k+1;
end;
n:=k; write (' искомое число x = [');
for k:=1 to n do write (a[k],',');
write (']');
end.
Слайд 11Результаты работы программы
1.8 = [1,1,4,0,]
1.6 = [1,1,1,1,1,0,0,]
1.65 = [1,1,1,1,5,1,75350303,2,3,1,1,0,0,]
7.3
ошибка 101 – выход за пределы размерности массива
2.5
= [2,2,0,] 4.75 = [4,1,3,0,0,]
Описание ошибок
В большинстве случаев из-за округления бесконечных периодических десятичных дробей происходит накопление погрешности.
В некоторых случаях зафиксирована некорректная работа функции trunс().
В некоторых случаях зафиксирована некорректная работа функции frac().
Реализация алгоритма разложения действительного числа в цепную дробь
Слайд 14Бенуа Мандельброт
– отец фракталов
французский математик, профессор математических наук, почетный
преподаватель Йельского Университета, научный сотрудник компании «IBM», Баттельский член Тихоокеанской
Национальной лаборатории.(1924 - 2010 )
Слайд 15Заключение
В процессе работы над проектом я
изучила много литературы о цепных дробях, научилась использовать их при
вычислении. Также в процессе работы я раскрыла свойства подходящих дробей, особенности разложения действительных чисел в неправильные дроби, погрешности, которые возникают в результате этого разложения, и применение теории цепных дробей для решения ряда алгебраических задач.В данном проекте работа показывает значение цепных дробей в математике. Зная цепную дробь, изображавшую действительное число, можно определить это число с достаточной точностью, успешно применять к решению неопределенных уравнений. Основная трудность при решении таких уравнений состоит в том, чтобы найти какое-нибудь его частное решение. Так вот, с помощью цепных дробей можно указать алгоритм для разыскания такого частного решения.
Цепные дроби можно применить и к решению более сложных неопределённых уравнений. Бесконечные цепные дроби могут быть использованы для решения алгебраических уравнений, для быстрого вычисления значений отдельных функций.
Цель своей работы считаю достигнутой, так как в ходе исследования мною была: изучена история цепных дробей и применение их при решении заданий.
А в настоящее время цепные дроби находят всё большее применение в вычислительной технике, и позволяют строить эффективные алгоритмы для решения задач.










![Презентация по математике на тему: Результаты работы программы1.8 = [1,1,4,0,] 1.6 = [1,1,1,1,1,0,0,]1.65 = [1,1,1,1,5,1,75350303,2,3,1,1,0,0,]7.3 ошибка 101 – выход за](/img/thumbs/336ff5fa734a4ceedbca1ed96ec196f2-800x.jpg)