Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение сечений многогранников геометрия 10 класс
Содержание
- 1. Построение сечений многогранников геометрия 10 класс
- 2. Обучающая цель: формирование умений и навыков построения
- 3. Структура урокаОрганизационный моментЦелеполагание и мотивацияАктуализация знанийИзучение нового материалаЗакреплениеДомашнее заданиеРефлексия.
- 4. Опора - памятка.Аксиома1. Через любые три точки,
- 5. Слайд 5
- 6. Параллелепипед имеетшесть гранейего сечениямимогут быть:Треугольники2) Четырёхугольники3) Пятиугольники4)Шестиугольники
- 7. При построении сечений параллелепипеда следует учитывать:Для построения
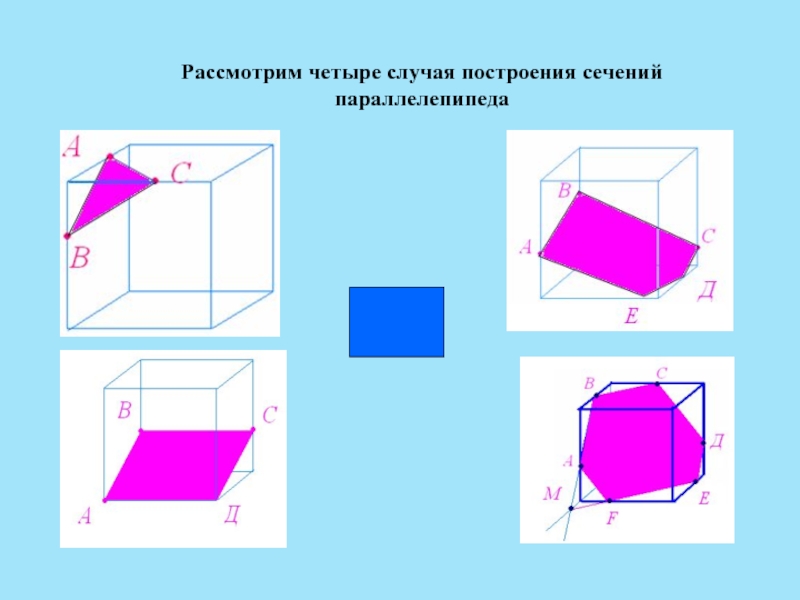
- 8. Рассмотрим четыре случая построения сечений параллелепипеда
- 9. АВАСВС1 случай
- 10. ДАВВССД || АВДА2 случай
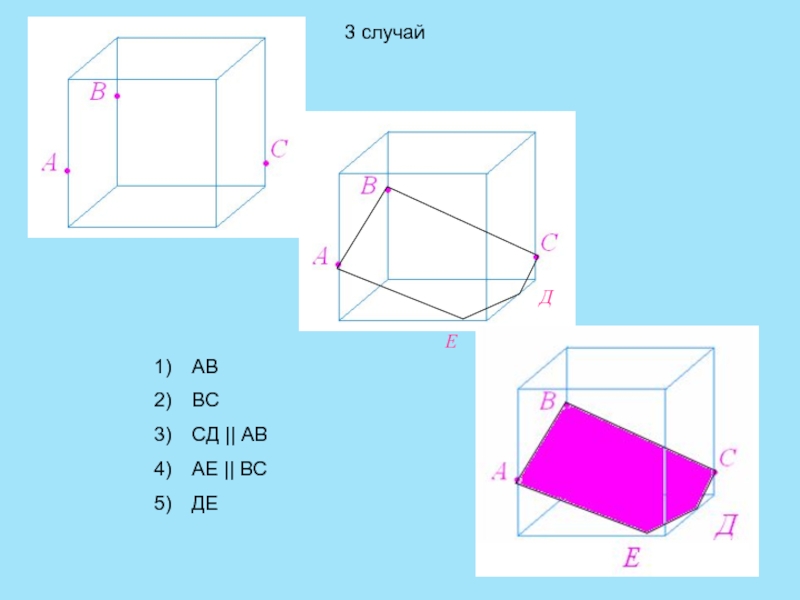
- 11. ДЕАВВССД || АВАЕ || ВСДЕ3 случай
- 12. 1)АВ2)ВС3)М4) МЕ || BC5) AF6) DE || AB7) CD4 случай
- 13. Следом называют прямую пересечения плоскости сечения и
- 14. Метод следов включает три важных пункта:Строим линию
- 15. NLMXNLMXKMLML ∩ D1 A1 =X1) XN ∩ B1 A1 = K2) MK
- 16. NLMKРТ1)ML ∩ DD12) KN ∩ D1 C13) PT4) NT5) LP
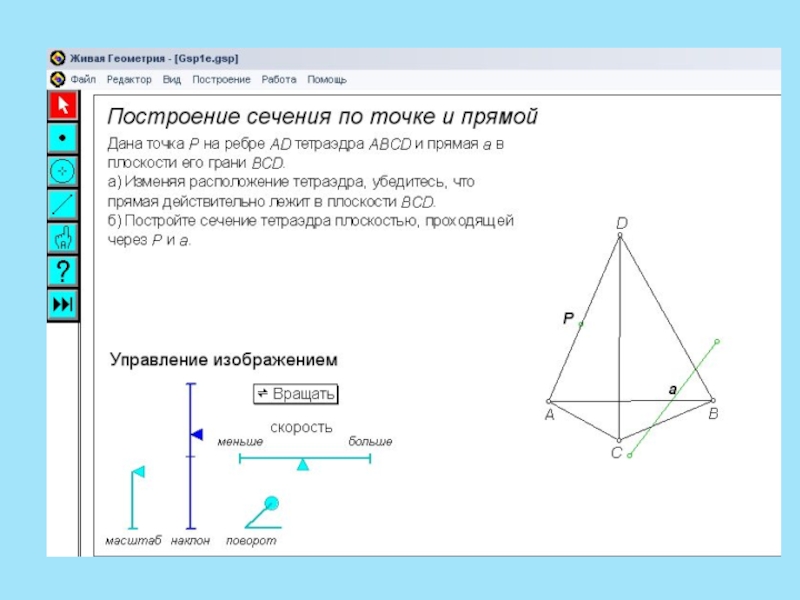
- 17. Самостоятельная работаПостроить сечения тетраэдра плоскостью, проходящие через
- 18. Решения задачПодведение итогов урокаДомашнее задание.
- 19. Метод внутреннего проектирования.Дополнительное изучениеПриложения
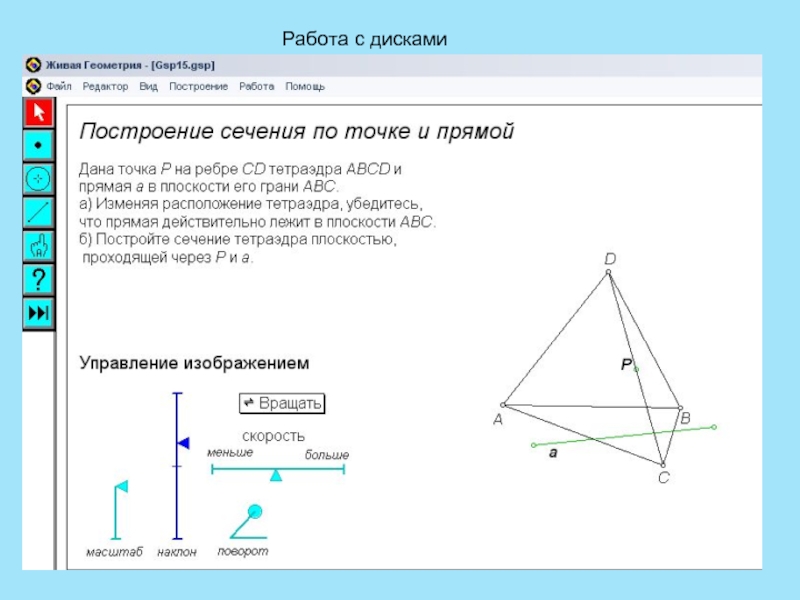
- 20. Работа с дисками
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Построение сечений многогранников
геометрия 10 класс
Выполнил: Старёв А. Е.
МОУ «Судская средняя
общеобразовательная школа №2» Череповецкого района
Слайд 2Обучающая цель: формирование умений и навыков построения сечений.
Развивающая цель: формирование
и развитие у учащихся пространственного представления.
Воспитывающая цель: добиваться поставленной цели
при решении задач.Слайд 3Структура урока
Организационный момент
Целеполагание и мотивация
Актуализация знаний
Изучение нового материала
Закрепление
Домашнее задание
Рефлексия.
Слайд 4Опора - памятка.
Аксиома1. Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и притом только одна.
Аксиома2. Если две
точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.Аксиома3. Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следствия из аксиом:
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Способы задания плоскости
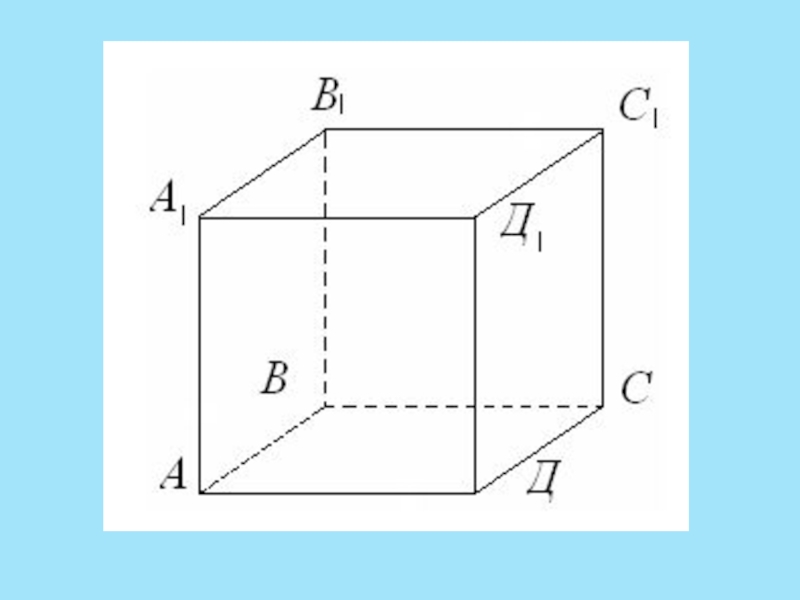
Слайд 6Параллелепипед имеет
шесть граней
его сечениями
могут быть:
Треугольники
2) Четырёхугольники
3) Пятиугольники
4)Шестиугольники
Слайд 7При построении сечений параллелепипеда следует учитывать:
Для построения сечений достаточно построить
точки пересечения секущей плоскости с рёбрами параллелепипеда, после чего остаётся
провести отрезки, соединяющие каждые две построенные точки, лежащие в одной и той же граниЕсли секущая плоскость пересекает
две противоположные грани по каким-то отрезкам, то эти отрезки параллельны
АВ || CD
AE || BC
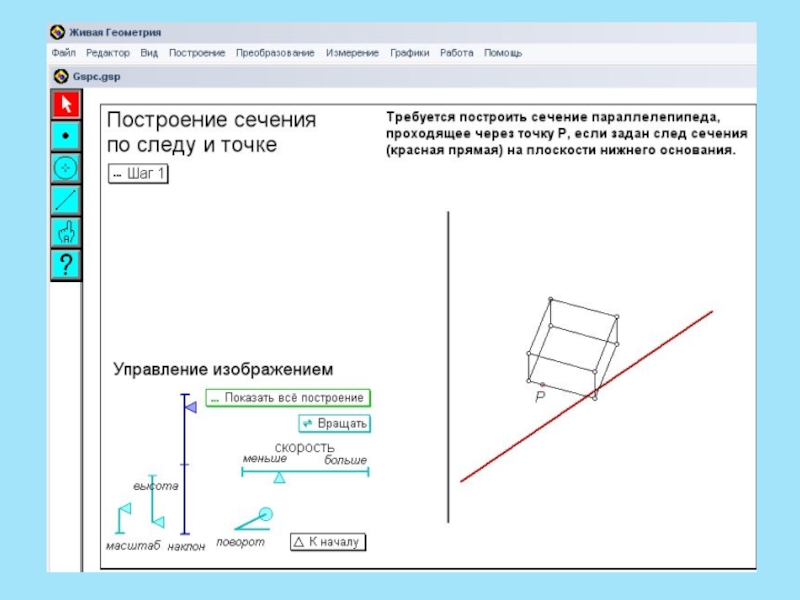
Слайд 13Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани
многогранника. Чтобы построить след, достаточно знать две его точки, т. е.
точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани. Если след построен, то отрезок , по которому он пересекается с плоскостью , дает сторону сечения, лежащую в этой плоскости. Но еще важнее то, что каждая точка его пересечения со стороной грани или ее продолжением лежит и в плоскости другой грани.А
Р
N
Слайд 14Метод следов включает три важных пункта:
Строим линию пересечения (след) секущей
плоскости с плоскостью основания многогранника
Находим точки пересечения секущей плоскости с
рёбрами многогранникаСтроим, заштриховываем сечения
Задача
Построить сечение куба, проходящее через точки M, N, L
N
L
M
Слайд 17Самостоятельная работа
Построить сечения тетраэдра плоскостью,
проходящие через точки
M, N, K
M,
N, P
1)
2)
Построить сечение куба плоскостью, проходящей через точки К, М,
Р3)