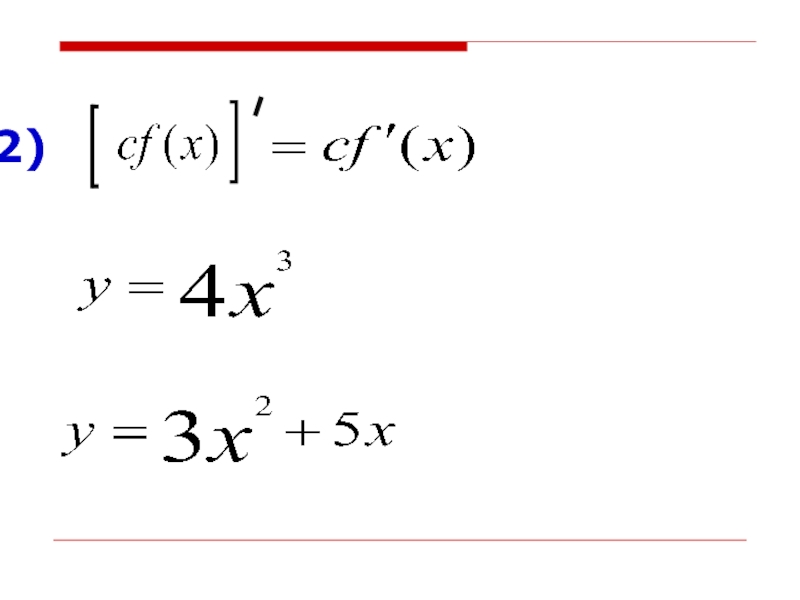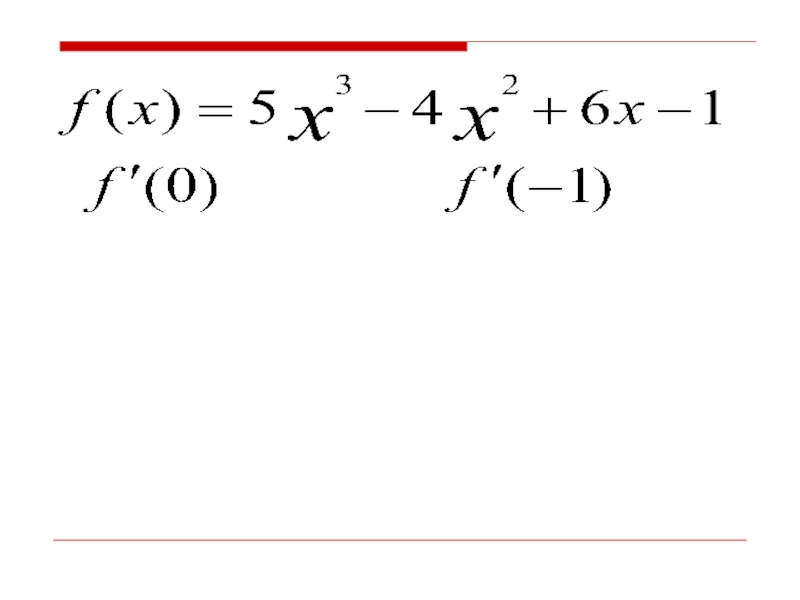Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока математики по теме "Понятие производной функции"
Содержание
- 1. Презентация для урока математики по теме "Понятие производной функции"
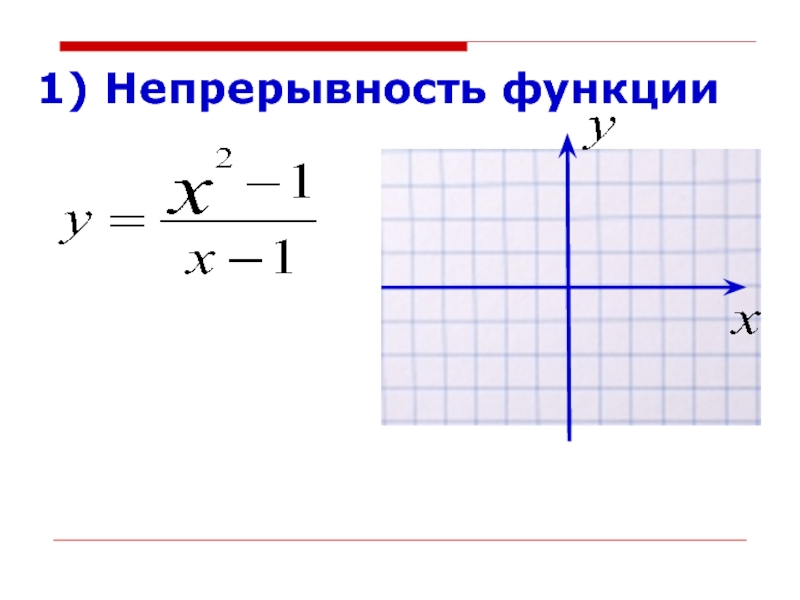
- 2. 1) Непрерывность функции
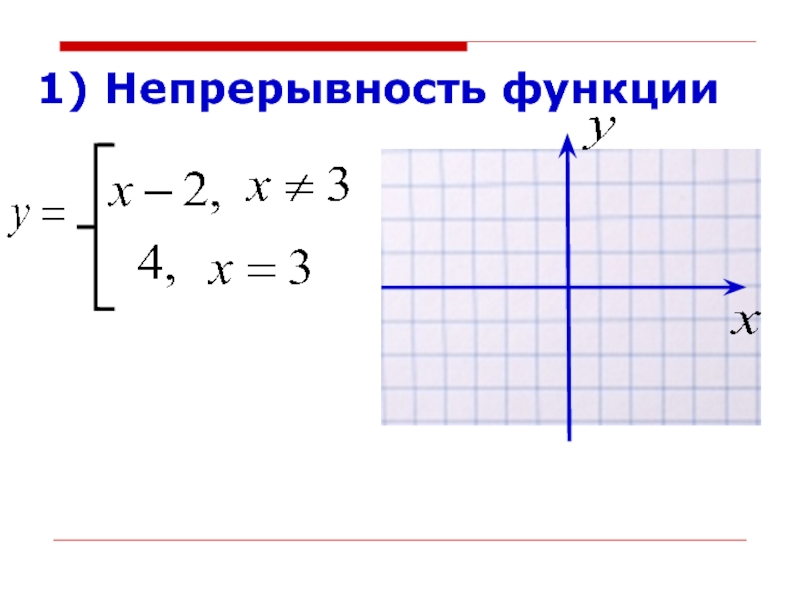
- 3. 1) Непрерывность функции
- 4. 1) Непрерывность функции
- 5. 1) Непрерывность функции
- 6. Непрерывность функции
- 7. 2) Производная функции
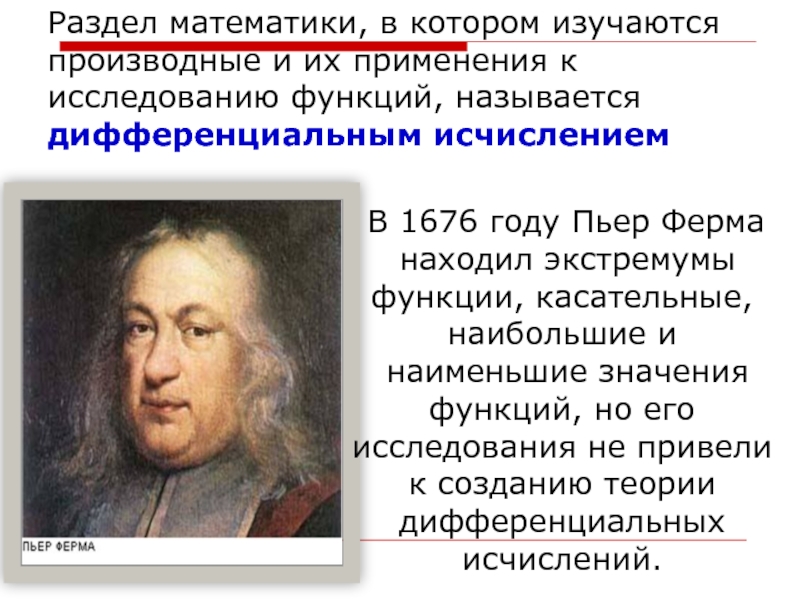
- 8. Раздел математики, в котором изучаются производные и
- 9. В 1736 году Исаак
- 10. Современник Ньютона Лейбниц предложил новый
- 11. И вот в 18 веке величайший математик
- 12. Для чего мы изучаем
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Операцию нахождения производной
- 26. Если функция имеет производную
- 27. Пример
- 28. Пример
- 29. Пример
- 30. Пример
- 31. Пример
- 32. Таблица
- 33. Примеры
- 34. №1 Найти
- 35. №1 Найти
- 36. №1 Найти
- 37. №1 Найти
- 38. №1 Найти
- 39. №1 Найти
- 40. №2 Используя определение
- 41. №3 Найти мгновенную скорость движения точки, если
- 42. №4 Найти мгновенную скорость движения точки, если
- 43. Слайд 43
- 44. 1)
- 45. 2)
- 46. Слайд 46
- 47. №18(2,4,6,8)Найти производные функций:
- 48. №18(2,4,6,8)Найти производные функций:
- 49. №18(2,4,6,8)Найти производные функций:
- 50. №18(2,4,6,8)Найти производные функций:
- 51. №19(2,4,6,8)Продифференцировать функции:
- 52. №19(2,4,6,8)Продифференцировать функции:
- 53. №19(2,4,6,8)Продифференцировать функции:
- 54. №19(2,4,6,8)Продифференцировать функции:
- 55. №20(2,4)Найти:
- 56. №20(2,4)Найти:
- 57. №21(2,4,6,8)Найти значения х , при которых производная функции f(x) равна нулю:
- 58. №21(2,4,6,8)Найти значения х , при которых производная функции f(x) равна нулю:
- 59. №21(2,4,6,8)Найти значения х , при которых производная функции f(x) равна нулю:
- 60. №21(2,4,6,8)Найти значения х , при которых производная функции f(x) равна нулю:
- 61. Домашнее задание Выучить определение
- 62. Скачать презентанцию
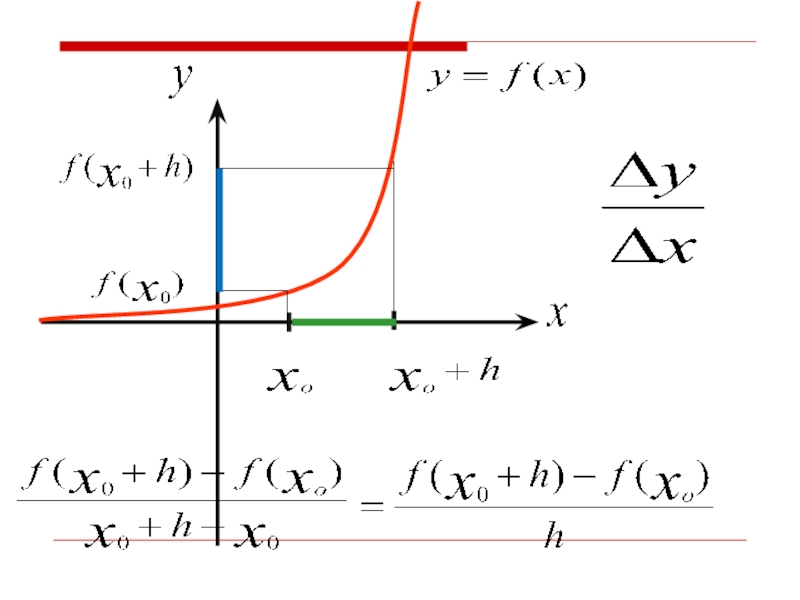
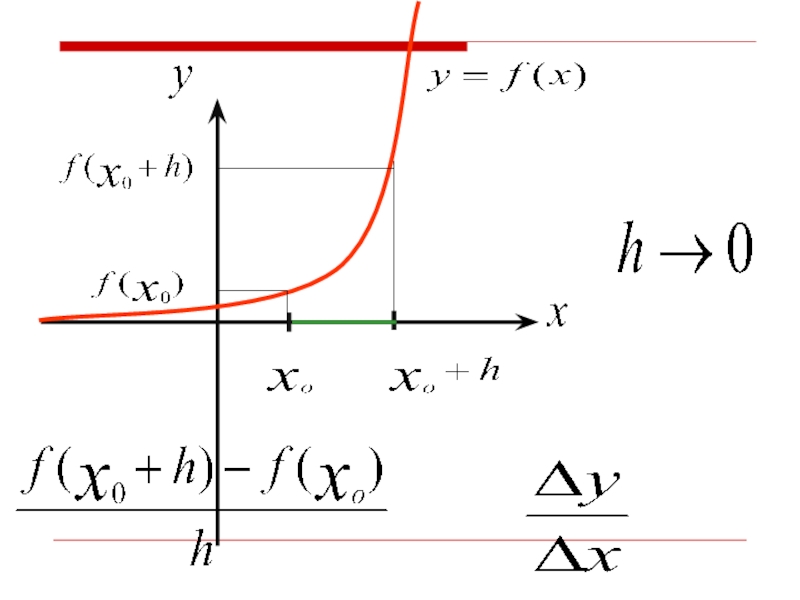
1) Непрерывность функции
Слайды и текст этой презентации
Слайд 8Раздел математики, в котором изучаются производные и их применения к
исследованию функций, называется дифференциальным исчислением
В 1676 году Пьер Ферма
находил экстремумы функции, касательные, наибольшие и
наименьшие значения функций, но его исследования не привели к созданию теории дифференциальных исчислений.
Слайд 9 В 1736 году Исаак
Ньютон назвал производную функции флюксией, а саму функцию
– флюентой. Он получил теорию дифференциальныхисчислений методом флюксий, но вся теория была осмыслена с точки зрения физики. Математики хотели строгих логических обоснований.
Слайд 10 Современник Ньютона Лейбниц предложил новый подход: он ввел
обозначения дифференциала, функции,такие понятия как ордината, абсцисса, координата. Но и
в его теории было много «темных» мест.
Слайд 11И вот в 18 веке величайший математик Леонард Эйлер создал
теорию дифференциальных и интегральных исчислений, и в таком виде она
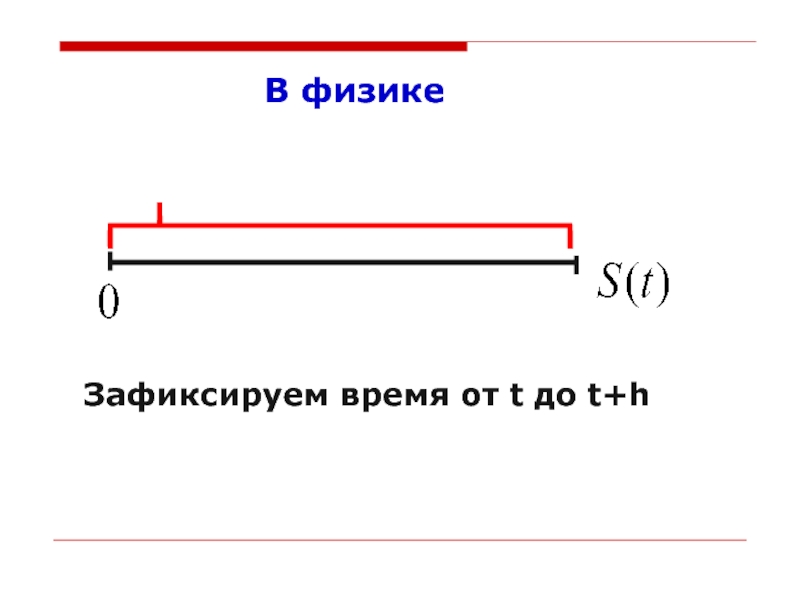
изучается и по сей день.
Слайд 17
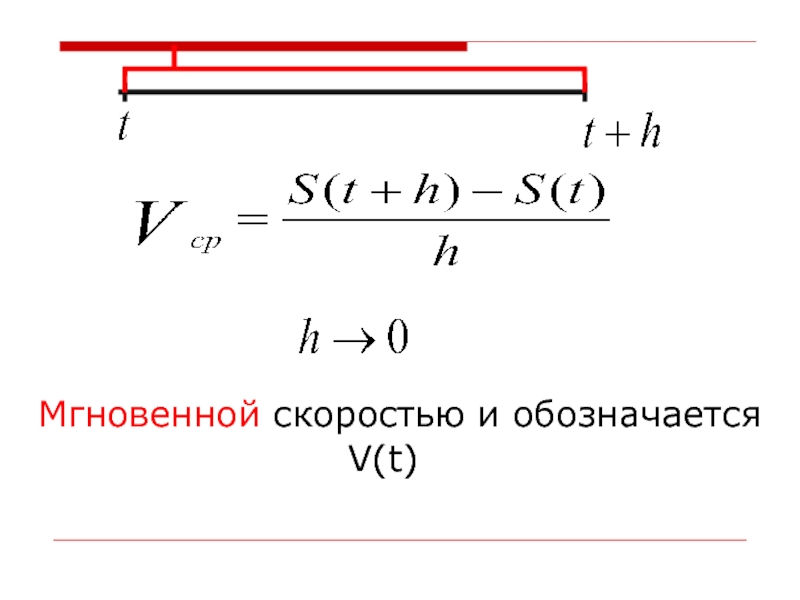
Мгновенная скорость
Мгновенную скорость V(t) называют производной функции S(t) и обозначают
Слайд 26
Если функция имеет производную в
точке х, то функция называется
дифференцированной
в этой точке.
Слайд 61 Домашнее задание
Выучить определение производной на оценку
№№
11(2), 12, 14(1),
18, 19, 20,21 - нечётные
