Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока "Теорема Пифагора"
Содержание
- 1. Презентация для урока "Теорема Пифагора"
- 2. Слайд 2
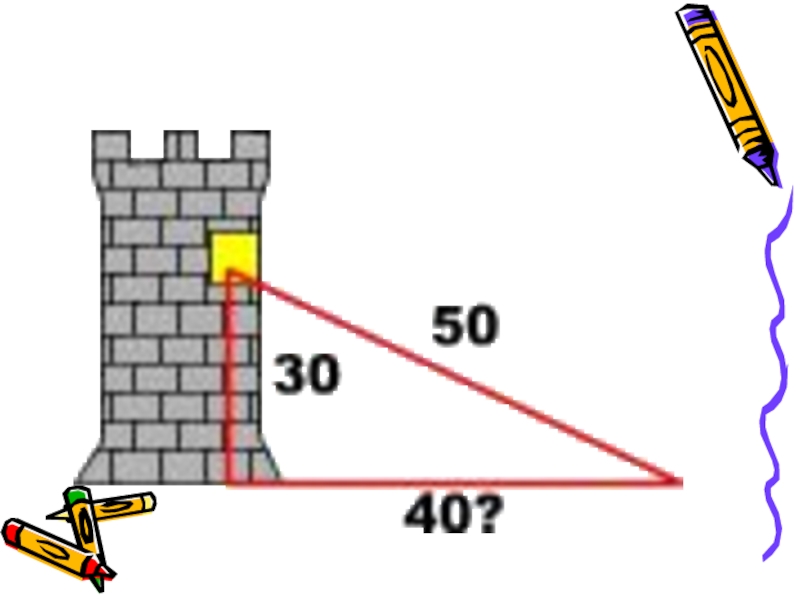
- 3. Найти а, в, с6ва4вс106апроверь45 °30°Устные задачи
- 4. ТЕОРЕМА ПИФАГОРА
- 5. "Геометрия обладает двумя великими сокровищами Первое-это теорема Пифагора..." содержание
- 6. Содержательная цель урока: -знакомство с теоремой Пифагора-знакомство
- 7. Знать зависимость между сторонами прямоугольного треугольника.Уметь доказывать теорему Пифагора.Уметь применять теорему Пифагора при решении задач. Планируемый результат:
- 8. План урока:Повторение пройденного материала.Сообщение о жизни Пифагора.Историческая
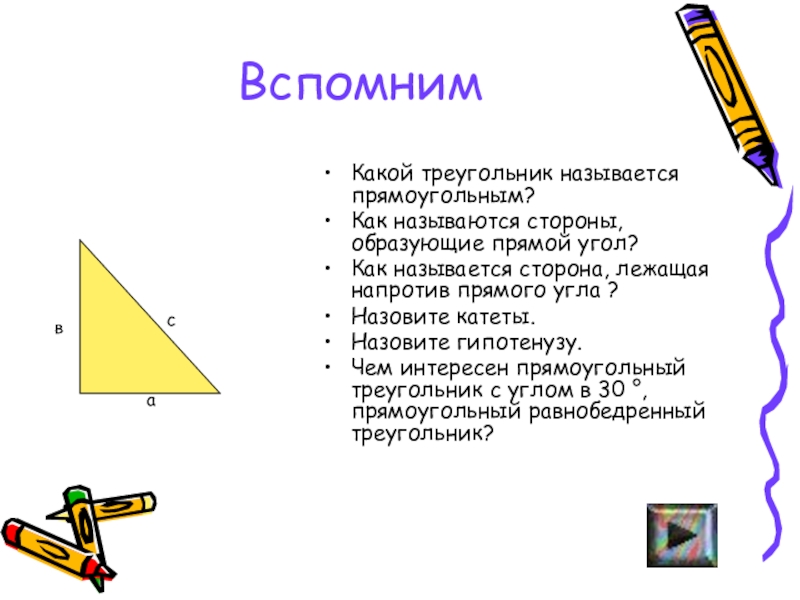
- 9. ВспомнимКакой треугольник называется прямоугольным?Как называются стороны, образующие
- 10. СОДЕРЖАНИЕ:
- 11. О Пифагоре сохранились десятки легенд
- 12. Мы не
- 13. Мыслитель, математик, философ Был
- 14. Пифагорейцы разделили математику на
- 15. В сферу
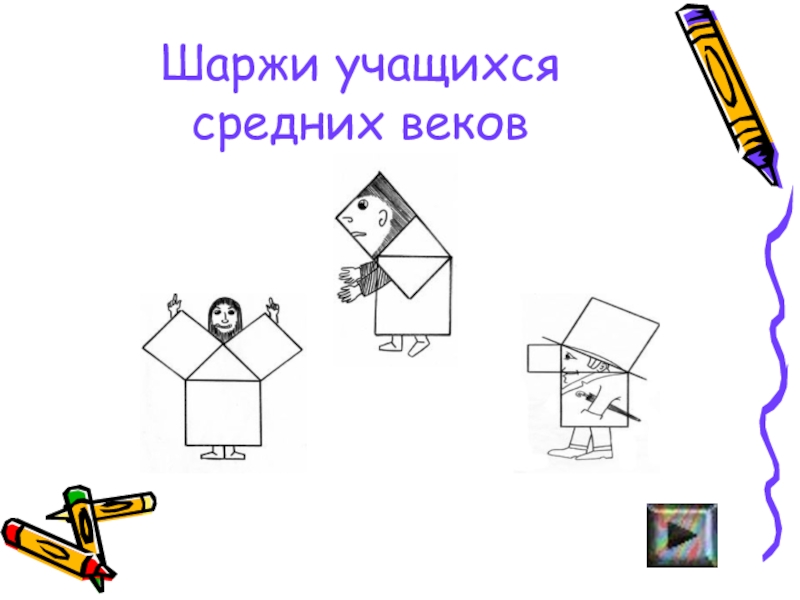
- 16. Теорема Пифагора считалась у учащихся средних
- 17. Шаржи учащихся средних веков
- 18. Гармония (греч. harmonia) означает "согласованность, соразмерность, единство
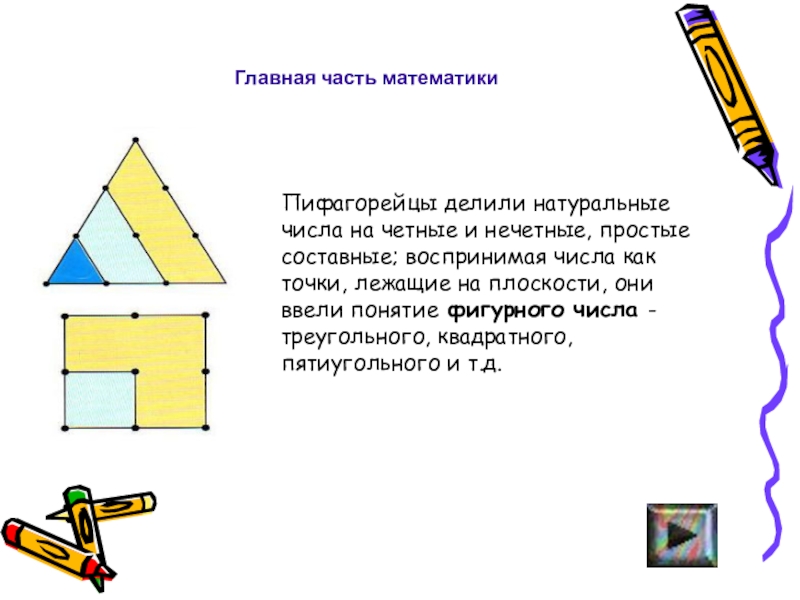
- 19. Главная часть математикиПифагорейцы делили натуральные числа на
- 20. Теорема Пифагора издавна широко применялась в разных
- 21. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.а2+в2=с2 содержание
- 22. Доказательство теоремы Дано: прямоугольный треугольник, а,в -
- 23. авс
- 24. "Да не войдет сюда не знающий
- 25. Устная задача 1. Существует ли прямоугольный треугольник
- 26. ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК Землемеры Древнего Египта для
- 27. Прямоугольные треугольники с целочисленными сторонами называют египетскими,
- 28. Старинные задачи, в которых будет «работать теорема
- 29. 2. задача индийского математика 12 в. Бхаскары:
- 30. 3. Над озером тихим, С полфута
- 31. О теореме ПифагораСуть истины вся в том
- 32. Проверь себя: ответыУстная задача 1 (да)Устная задача 2 ( 10см )Устная задача 3Устные задачисодержаниеСтаринные задачи
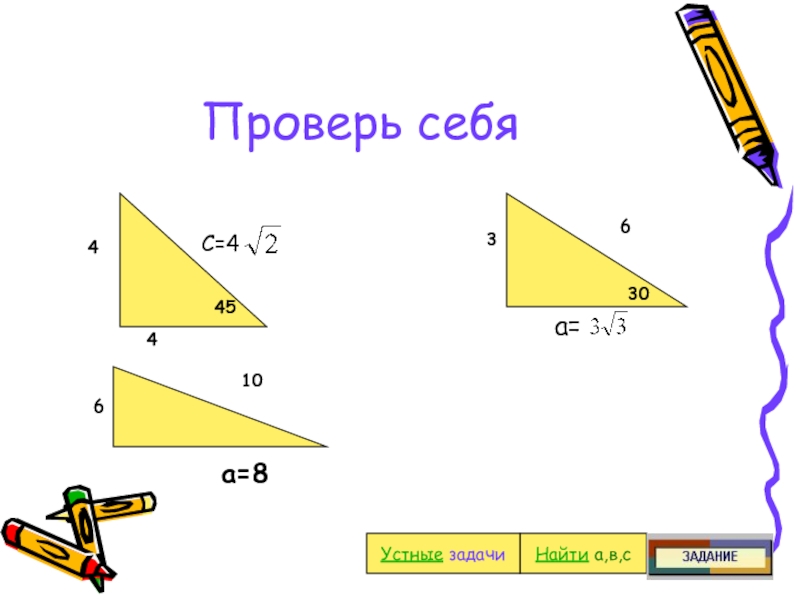
- 33. Проверь себя63034454С=4 2106а=8Найти а,в,сС=4а=Устные задачи
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. МОЛОДЕЦСтаринная задача 2Старинная задача 1Старинная задача 3
- 39. ТЫ ОШИБАЕШЬСЯСтаринная задача 3Старинная задача 2Старинная задача 1
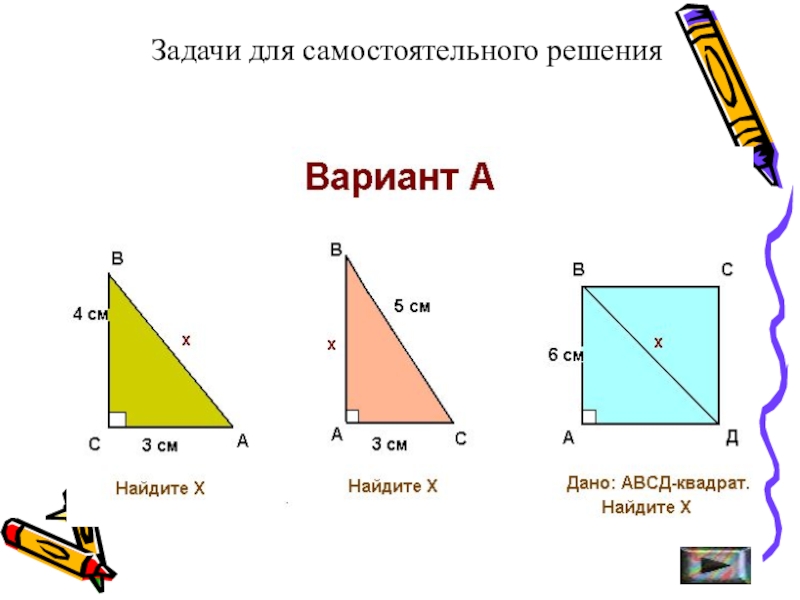
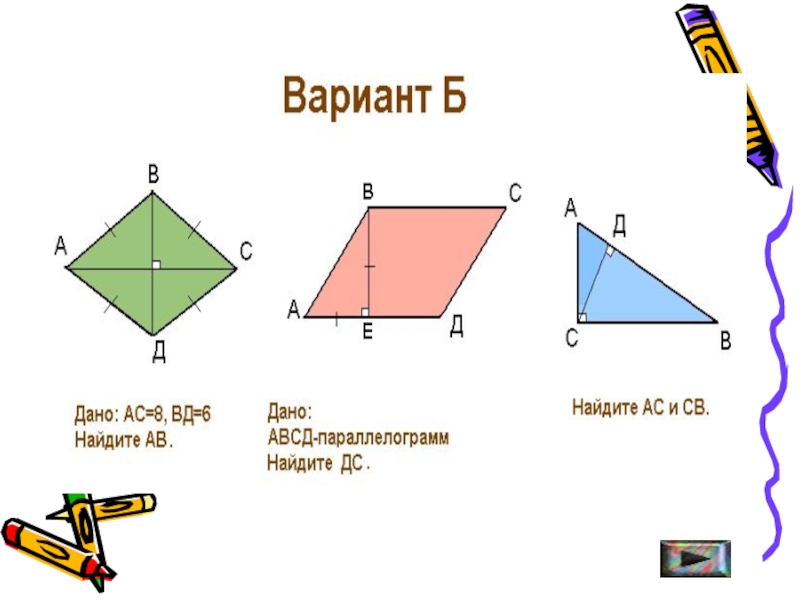
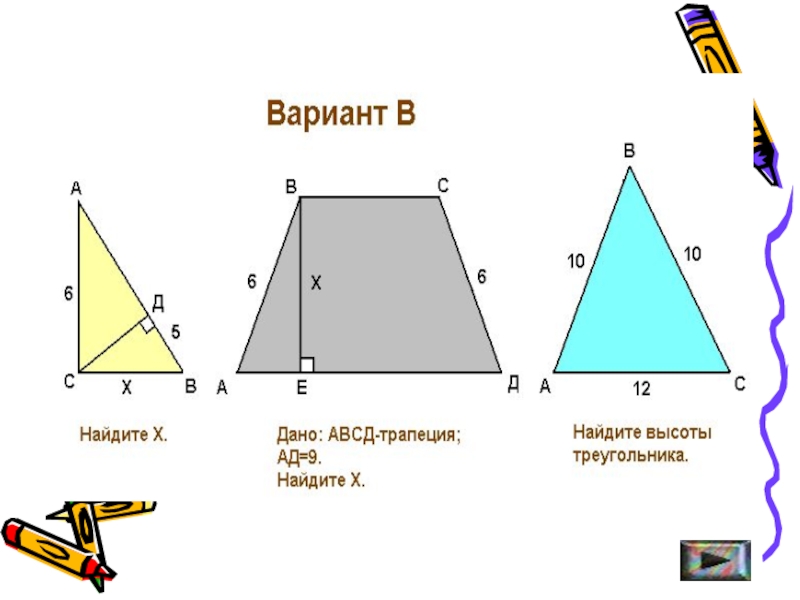
- 40. Задачи для самостоятельного решения
- 41. Слайд 41
- 42. Слайд 42
- 43. Верно ли утверждение «если квадрат
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 6
Содержательная цель урока:
-знакомство с теоремой Пифагора
-знакомство с основными этапами
жизни и деятельности Пифагора.
теорему Пифагора при решении задач. Слайд 7Знать зависимость между сторонами прямоугольного треугольника.
Уметь доказывать теорему Пифагора.
Уметь применять
теорему Пифагора при решении задач.
Планируемый результат:
Слайд 8План урока:
Повторение пройденного материала.
Сообщение о жизни Пифагора.
Историческая справка о теореме
Пифагора.
Работа над теоремой.
Решение задач с применением теоремы.
Подведение итога урока.
Домашнее задание.
Слайд 9Вспомним
Какой треугольник называется прямоугольным?
Как называются стороны, образующие прямой угол?
Как называется
сторона, лежащая напротив прямого угла ?
Назовите катеты.
Назовите гипотенузу.
Чем интересен прямоугольный
треугольник с углом в 30 °, прямоугольный равнобедренный треугольник? а
в
с
Слайд 11 О Пифагоре сохранились десятки легенд и мифов, с
его именем связано многое в математике и в первую очередь,
конечно, теорема, носящая его имя, которая занимает важнейшее место в школьном курсе геометрии.содержание
Слайд 12
Мы не знаем даже точных
дат его рождения и смерти: по некоторым данным Пифагор родился
около 580 г. и умер в 500 г. до н.э. Родившись на острове Самос, расположенном у самых берегов Малой Азии, от путешественников и капитанов кораблей он узнавал о близких и далеких чудесных странах Египта и Вавилонии, мудрость жрецов которых изумляла молодого Пифагора и манила. Совсем юным он покинул родину, сначала приплыв к берегам Египта, где 22 года внимательно присматривался к окружающим, прислушивался к жрецам. В Египте, рассказывают, Пифагор попал в плен к Камбизу, персидскому завоевателю, и его увели в Вавилон. Грандиозная панорама города, раскинувшего свои дворцы и высокие оборонительные стены по обоим берегам Ефрата, привела Пифагора в восторг и изумление. Он быстро осваивается со сложными вавилонскими традициями, у халдейских магов и жрецов изучает теорию чисел. И, может быть, отсюда пошла та числовая мистика приписывания числам божественной силы, которая Пифагором была преподнесена как философия. После возвращения на Самос он создал свою школу (лучше назвать – секту, общину), которая преследовала не только научные, но и религиозно-этические и политические цели. Деятельность союза была окружена тайной, и все научные открытия, сделанные пифагорейцами, приписывались самому Пифагору.Слайд 13Мыслитель, математик, философ
Был учеником Анаксимандра
и Ферекида. Имел красивую внешность, носил длинную бороду, а на
голове золотую диадему. Во время пребывания в Египте учился у жреца Ониуфиса из Гелиополя. Жил на острове Самос, а также в городе Кротон на юге Италии, где учредил философское общество, члены которого впервые занялись математикой как "чистой наукой".Пифагор - это не имя, а прозвище, которое о философ получил за то, что всегда говорил верно и убедительно, как греческий оракул.(Пифагор - "убеждающий речью";этимология восходит к Аполлону Пифийскому.) Своими речами приобрел 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Утверждал, что числа управляют звуками, гармоническое сочетание которых пленяет слух. По утрам философ, прежде чем приступить к занятиям с учениками, успокаивал душу игрой на лире. По одной из легенд, Пифагор говорил, что, пребывая вне тела, он слышал небесную мелодию. Первым ввел понятия философия (любомудрие) и космос. Сформулировал теорему, носящую его имя: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов".
Слайд 14 Пифагорейцы разделили математику на философию, арифметику, геометрию,
астрономию ,гармонию.
По этим дисциплинам и проводятся состязания между
участниками праздника, в ходе которых определяются достойные члены союза мудрейших.Слайд 15
В сферу интересов членов союза
входили научные исследования, религиозно - философские искания, политическая деятельность. Они
вели суровый образ жизни, превыше всего ценили самообладание, смелость и коллективную дисциплину. Пифагорейцы жили вместе, у них было совместное имущество, и даже свои открытия они считали общим достоянием.Краеугольным камнем философии пифагорейцев было мистическое учение о числе: числа руководят миром, числа лежат в основе вещей, числа - основа мира. У пифагорейцев появились экзотические числа: квадратные и треугольные, дружественные и совершенные, четно - четные, нечетно - нечетные, пятиугольные, кубические, пиромедальные.
Числам поклонялись, так как они служили гармонии, которую превыше всего ценили пифагорейцы.
Символом пифагорейской школы была пятиконечная звезда,
пентограмма.
"Все есть число ,"- говорили пифагорейцы, и при изучении геометрии их особенно интересовали числовые соотношения.
К математическим наукам пифагорейцы относили арифметику, геометрию, астрономию... и музыку! Они установили, что высота звучания струны зависит от ее длины, то есть опять же от числа! И создали первую математическую теорию музыки.
Слайд 16
Теорема Пифагора считалась у учащихся средних веков очень трудной
и называлась иногда- ослиный мост или- бегство убогих, т. к
. некоторые "убогие" ученики, не имевшие серьезной подготовки, бежали от геометрии .Слабые ученики, заучившие теорему наизусть без понимания и прозванные поэтому "ослами", не были в состоянии преодолеть теорему Пифагора, служившую для них вроде непроходимого моста . Теорему Пифагора учащихся называли так же "ветряной мельницей", составляли стихи вроде:« Пифагоровы штаны во все стороны равны».
Слайд 18
Гармония (греч. harmonia) означает "согласованность, соразмерность, единство частей и целого,
обуславливающее внутреннюю и внешнюю формы предмета, события, явления, их совершенство".
Пифагорейцы
считали, что Земля имеет форму самого совершенного тела - шара и находится в центре Вселенной. Остальные известные им планеты - Солнце, Луна, Меркурий, Венера, Марс, Юпитер и Сатурн - движутся вокруг нее. При этом расстояние от Земли до каждой из планет таково, что вместе они составляют семиструнную арфу, и при их движении возникает прекрасная музыка сфер. Обычные люди не слышат ее из-за суеты жизни и могут наслаждаться ею лишь после смерти. Великий Пифагор слышал ее и при жизни.Во всем царит гармонии закон
И в мире все суть ритм, аккорд и тон
Дж.Драйден
Слайд 19Главная часть математики
Пифагорейцы делили натуральные числа на четные и нечетные,
простые составные; воспринимая числа как точки, лежащие на плоскости, они
ввели понятие фигурного числа - треугольного, квадратного, пятиугольного и т.д.Слайд 20Теорема Пифагора издавна широко применялась в разных областях науки. О
ней писали в своих произведениях римский архитектор и инженер Витрувий,
греческий писатель Плутарх, математик Прокл.Слайд 21
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
а2+в2=с2
содержание
Слайд 22Доказательство теоремы
Дано: прямоугольный треугольник, а,в - катеты, с-гипотенуза
Доказать: а2+в2=с2
Доказательство:
Рассмотрим прямоугольный треугольник с
катетами а, в и гипотенузой с. Достроим его до квадрата со стороной а+в.Площадь этого квадрата равна (а+в)2.
С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна 1/2ав, и квадрата со стороной с, поэтому S=4*1/2ав+с2=2ав+с2.
Таким образом, (а+в)2=2ав+с2, откуда
а2+2ав+в2-2ав=с2
а2+в2=с2.
Теорема доказана.
Слайд 24 "Да не войдет сюда не знающий геометрии" (Платон)
Пифагорейцами была создана геометрия прямолинейных фигур, учение о подобии, введен
принцип математического доказательства.Задание
Используйте чертеж (рис.а), восстановите доказательство теоремы Пифагора, которое приписывают индийскому математику и астроному Ариабхате (467 - ок.550 гг.)
Слайд 25Устная задача 1. Существует ли прямоугольный треугольник со сторонами 3м,4м и
5м?
Устная задача 2.
Стороны прямоугольника 6 см и 8 см.Чему равна
диаго-
наль этого прямоугольника?Устная задача 3.
В прямоугольном треугольнике a,b-катеты,c-гипотенуза Заполните пустые клеточки таблицы:
проверь
Слайд 26
ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК
Землемеры Древнего Египта для построения прямого угла
пользовались следующим приёмом. Бечёвку узлами делили на 12 равных частей
и концы связывали. Затем бечёвку растягивали на Земле так, что получался треугольник со сторонами 3,4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой. В связи с указанным способом построения прямого угла треугольник со сторонами 3,4 и 5 ед. называют египетским..
Слайд 27Прямоугольные треугольники с целочисленными сторонами называют египетскими, а тройки целых
чисел, для которых выполняется соотношение, связывающее стороны прямоугольного треугольника, –
пифагоровыми тройками.Проверь, являются ли пифагоровыми следующие тройки чисел:
3, 4, 5
5, 12, 13
7, 24, 25?
Придумай два-три примера египетских треугольников, стороны которых образуют пифагоровы тройки.
содержание
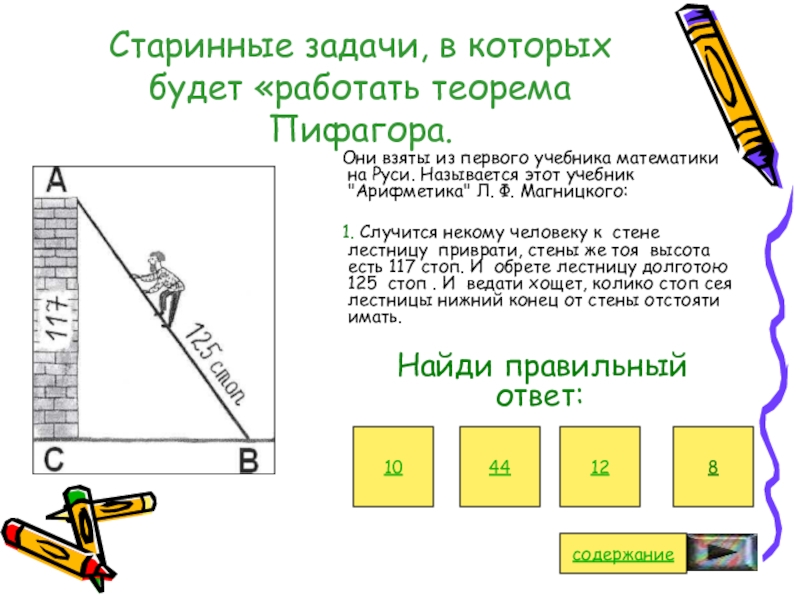
Слайд 28Старинные задачи, в которых будет «работать теорема Пифагора.
Они взяты из первого учебника математики на Руси.
Называется этот учебник "Арифметика" Л. Ф. Магницкого:1. Случится некому человеку к стене лестницу приврати, стены же тоя высота есть 117 стоп. И обрете лестницу долготою 125 стоп . И ведати хощет, колико стоп сея лестницы нижний конец от стены отстояти имать.
Найди правильный ответ:
содержание
10
12
44
8
Слайд 292. задача индийского математика 12 в. Бхаскары:
На берегу реки рос тополь одинокий. Вдруг ветра
порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота?ПРОВЕРЬ СЕБЯ:
содержание
1,5
4
8
10
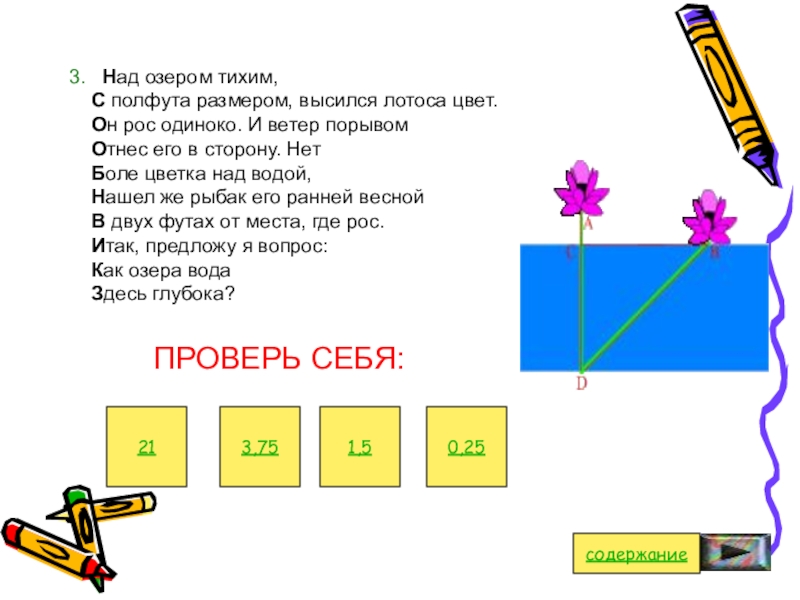
Слайд 30 3. Над озером тихим, С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом Отнес его в сторону.
Нет Боле цветка над водой, Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода Здесь глубока?ПРОВЕРЬ СЕБЯ:
содержание
1,5
3,75
0,25
21
Слайд 31О теореме Пифагора
Суть истины вся в том , что она-
навечно,
Когда хоть раз в прозрении ее увидим свет,
И теорема Пифагора
через столько летДля нас. Как для него, бесспорна, безупречна.
А. Шамиссо
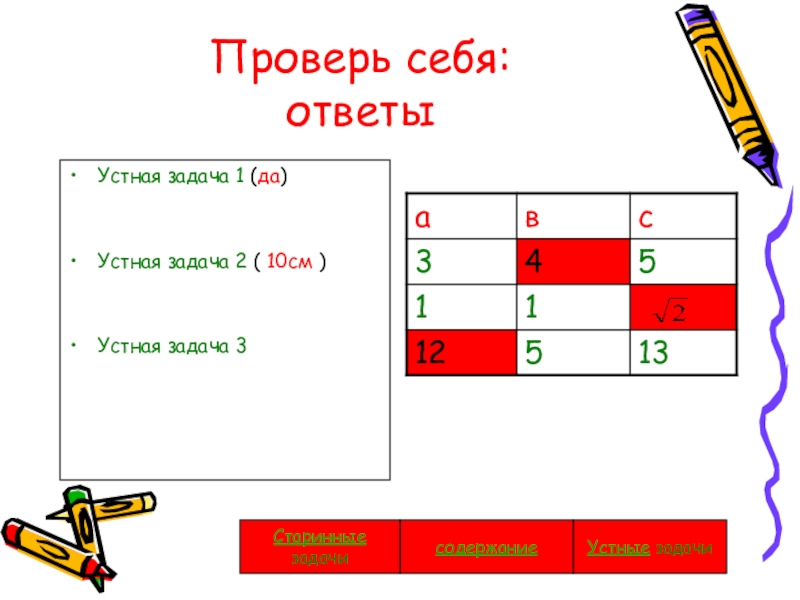
Слайд 32Проверь себя:
ответы
Устная задача 1 (да)
Устная задача 2 ( 10см )
Устная
задача 3
Устные задачи
содержание
Старинные задачи
Слайд 34
1 вариант
1. Диагонали ромба равны 14 см и 48
см. Найдите сторону ромба.2. В треугольнике два угла равны 45ºи 90 º, а большая сторона-20 см. Найдите две другие стороны треугольника.
2 вариант
1. Стороны треугольника равны 8 см и 12 см. Найдите его диагональ.
2. В треугольнике АВС ∠ А=90 º, ∠ В=30 º, АВ=6 см. Найдите стороны треугольника.
1 уровень
Слайд 35
1 вариант
1. В прямоугольной трапеции основания равны
5 см и 17 см, а большая боковая сторона-13 см. Найдите площадь трапеции.2. В треугольнике две стороны равны 10 см и 12см, а угол между ними 45 º. Найдите площадь треугольника.
2 вариант
В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание -20 см. Найдите площадь трапеции.
2. В треугольнике две стороны равны 12 см и 8 см, а угол между ними 60 º. Найдите площадь треугольника.
2 уровень
Слайд 36
1 вариант
1. В прямоугольной трапеции основания равны
5 см и 17 см, а большая боковая сторона-13 см. Найдите площадь трапеции.2. В треугольнике две стороны равны 10 см и 12см, а угол между ними 45 º. Найдите площадь треугольника.
2 вариант
В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание -20 см. Найдите площадь трапеции.
2. В треугольнике две стороны равны 12 см и 8 см, а угол между ними 60 º. Найдите площадь треугольника.
2 уровень
Слайд 37
1 вариант
1. В параллелограмме АВСД ВД=2 41 см, АС=26
см, АД=16 см. Через точку О- точку пересечения диагоналей параллелограмма проведена прямая, перпендикулярная стороне ВС. Найдите отрезки, на которые эта прямая разделила сторону АД.2. В треугольнике АВС АВ=ВС. Высота АК делит сторону ВС на отрезки ВК=24 см и КС=1 см. Найдите площадь треугольника и сторону АС.
2 вариант
1. Две окружности радиусами 13 см и 15 см пересекаются. Расстояние между их центрами О1 и О2 равно 14 см. Общая хорда этих окружностей АВ пересекает отрезок О1О2 в точке К. Найдите О1К и КО2 (О1- центр окружности радиусом 13 см).
2. В треугольнике АВС АВ=АС. Высота ВМ=9 см и делит сторону АС на два отрезка так, что АМ=12 см. Найдите площадь и периметр треугольника.
3 уровень
содержание
Слайд 43 Верно ли утверждение «если квадрат какой-либо стороны треугольника
равен сумме квадратов длин двух других его сторон, то этот
треугольник прямоугольный»??