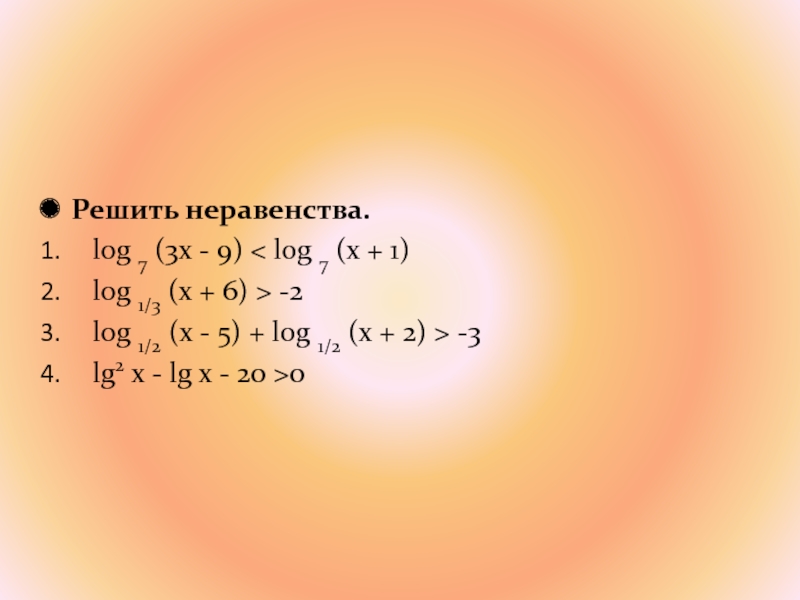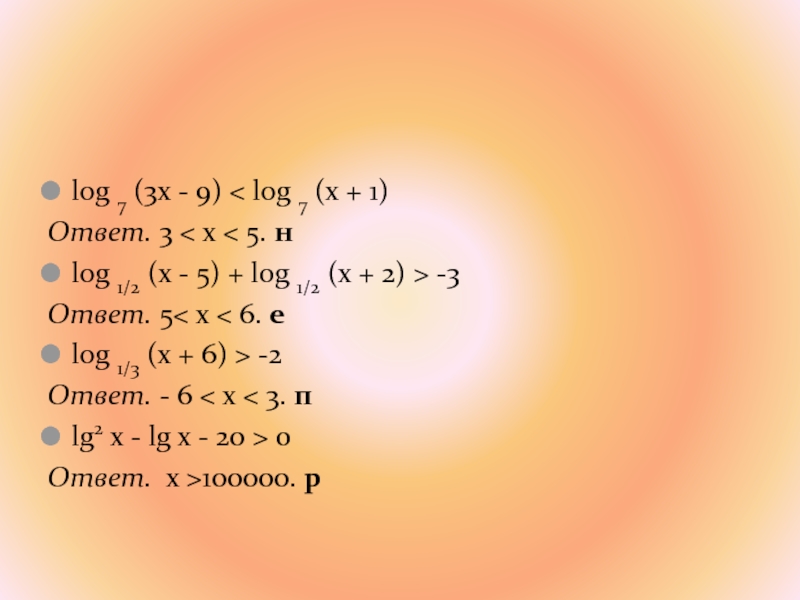Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по математике на тему "Логарифмы".
Содержание
- 1. Презентация по математике на тему "Логарифмы".
- 2. Урок «Логарифмы»Подготовила и провела:Размарилова Татьяна Ивановна, учитель математики высшей квалификационной категории
- 3. Тема: « Логарифмы».Тип урока: урок обобщения и
- 4. Учебно-методический комплекс1. Учебник: Алгебра и начала математического
- 5. Задачи урокаПредметные: добиться усвоения учащимися систематических, осознанных
- 6. Методы обучения: частично-поисковый, исследовательскийПедагогические технологии: личностно-ориентированное обучение, проектный метод.Форма работы: фронтальная, индивидуальная, групповая
- 7. Оснащение урока:Мультимедийный проекторМаркерная доскаПрезентации, подготовленные учителем и
- 8. Ход урока:Организационный моментВступительное слово учителяПредставление
- 9. Логарифмы Холодные числа, внешне сухие формул
- 10. В чем проявляется взаимосвязь развития математической науки
- 11. Значимость логарифмов «С точки зрения вычислительной практики,
- 12. Из истории логарифмов Слово логарифм происходит
- 13. Лаборатории
- 14. Лаборатория теоретиков
- 15. Логарифмом положительного числа b по основанию a,
- 16. В зависимости от значения основания приняты два
- 17. Можно выделить три формулыИз определения логарифма следует следующее тождество:Примеры:
- 18. 1. Логарифм произведения равен сумме логарифмов множителей:2. Логарифм частного равен разности логарифмов :
- 19. 3. Логарифм степени равен произведению показателя степени
- 20. 5. Переход от одного основания к другому
- 21. 1. Вычислить: 2. Вычислить: а) 16
- 22. ответы1. 1(в)2. 64(б)3. (а)4. 1,5 (г)
- 23. Исследовательская лабораторияЧто же такое логарифм?
- 24. ГРАФИКИ И СВОЙСТВА ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ1)
- 25. 1)
- 26. Свойства функции:Область определения (0; ∞)Область значений RЧётность
- 27. Применение логарифмической функцииЛогарифмическая функция крайне важна в
- 28. Выводы: Логарифмической функцией называется функция вида f(x) = log а x, определённая при
- 29. РЕШИТЕ ПРИМЕРЫ, ОСНОВЫВАЯСЬ НА СВОЙСТВА ЛОГАРИФМА. ПРИ
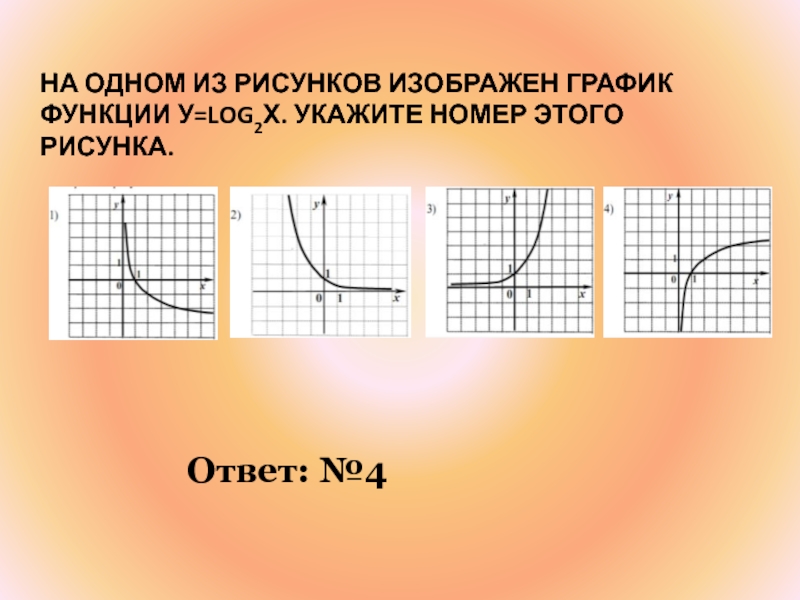
- 30. НА ОДНОМ ИЗ РИСУНКОВ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ У=LOG2Х. УКАЖИТЕ НОМЕР ЭТОГО РИСУНКА. Ответ: №4
- 31. Лаборатория мыслителей
- 32. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ Уравнения, содержащие переменную
- 33. МЕТОДЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙФункционально-графический С использованием определенияПотенцированиеВведение новой переменнойЛогарифмирование обеих частей уравнения, если они положительны
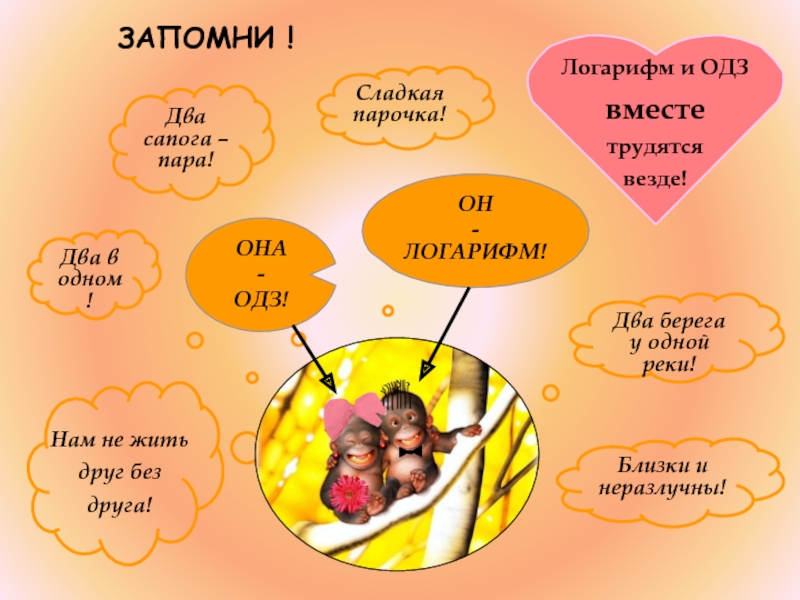
- 34. ЗАПОМНИ !Сладкая парочка!Два в одном!Два берега у
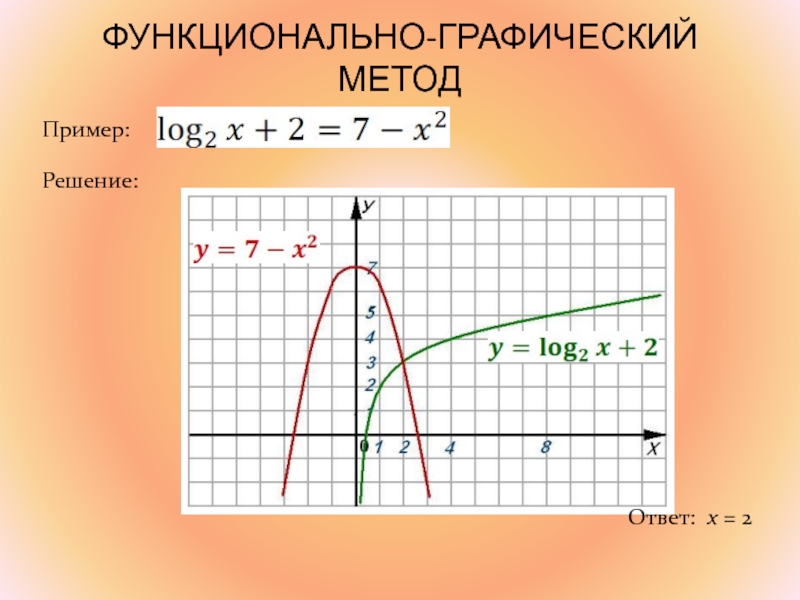
- 35. ФУНКЦИОНАЛЬНО-ГРАФИЧЕСКИЙ МЕТОДПример:Решение:Ответ: x = 2
- 36. МЕТОД С ИСПОЛЬЗОВАНИЕМ ОПРЕДЕЛЕНИЯПример:Решение:
- 37. ПОТЕНЦИРОВАНИЕПример: Решение:
- 38. ВВЕДЕНИЕ НОВОЙ ПЕРЕМЕННОЙПример:Решение:
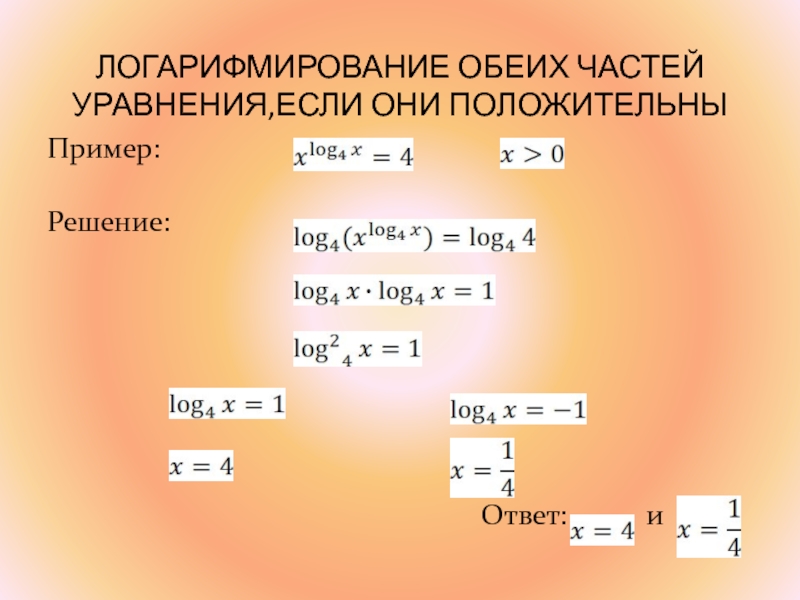
- 39. ЛОГАРИФМИРОВАНИЕ ОБЕИХ ЧАСТЕЙ УРАВНЕНИЯ,ЕСЛИ ОНИ ПОЛОЖИТЕЛЬНЫПример:Решение:
- 40. Работа у доски с проверкой
- 41. Работа у доски с проверкой
- 42. Экспериментальная лаборатория
- 43. Логарифмические неравенства
- 44. Логарифмическим неравенством называют неравенства вида logaf(x) >
- 45. При решении логарифмических неравенств следует учитывать общие
- 46. Традиционный способ
- 47. Традиционный способ
- 48. Индивидуальная работа по теме:Вариант 1:1.2.Вариант 2:1.2.Вариант 3:1.2.
- 49. ОтветыВариант 1:Вариант 2:Вариант 3:
- 50. Работа у доски Решение неравенств log3 (2х-4)>log3(14-x)Log1/3(2х-4)>log1/3(14-x)6
- 51. Практическая лаборатория
- 52. Логарифмы в деятельности человекав животноводстве
- 53. Логарифмы в природераковинагалактикасемечки подсолнухапаутинарога козла
- 54. Логарифмическая спираль – единственный тип спирали, не
- 55. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали
- 56. Рога животных растут лишь с одного конца.
- 57. Также происходит рост раковин морских животных .
- 58. По логарифмической спирали формируется тело циклона
- 59. По логарифмическим спиралям закручены и многие галактики, в частности – Галактика Солнечной системы.
- 60. Логарифмы в музыке«… Даже изящные искусства питаются
- 61. Музыканты редко увлекаются математикой, но
- 62. Слайд 62
- 63. Логарифмы в живописи Логарифмические линии в
- 64. “Музыка может возвышать или умиротворять душу, Живопись
- 65. Продукт исследований
- 66. Слайд 66
- 67. Слайд 67
- 68. Домашнее задание
- 69. Дополнительные задания
- 70. Решить неравенства.log 7 (3x - 9) <
- 71. log 7 (3x - 9) < log
- 72. Слайд 72
- 73. рефлексияПродолжите фразу:“Сегодня на уроке я узнал…” “Сегодня
- 74. СПАСИБОЗА РАБОТУ!
- 75. СПАСИБО ЗА УРОК!!!
- 76. Судьба Вселенной в ваших руках!До свидания!
- 77. Скачать презентанцию
Урок «Логарифмы»Подготовила и провела:Размарилова Татьяна Ивановна, учитель математики высшей квалификационной категории
Слайды и текст этой презентации
Слайд 2Урок «Логарифмы»
Подготовила и провела:
Размарилова Татьяна Ивановна,
учитель математики высшей квалификационной
категории
Слайд 3Тема: « Логарифмы».
Тип урока: урок обобщения и систематизация знаний.
Продолжительность
урока: 2 часа
Цель урока: закрепить, обобщить и систематизировать знания и
умения учащихся в вычислении логарифмов, логарифмических уравнений и неравенств.Слайд 4Учебно-методический комплекс
1. Учебник: Алгебра и начала математического анализа. 10 класс:
учебник для общеобразовательных учреждений: базовый и профильный уровни \(Ю.М. Колягин,
М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин); под редакцией А.Б. Жижченко. –2 издание.-М.: Просвещение ,2009.
2. Методические пособия: Книга для учителя. Изучение алгебры и начал математического анализа в 10 классе: \ Н.Е. Федорова, М.В. Ткачева. – М.: Просвещение ,2009.
3. Дидактические материалы. 10 класс: профильный уровень/ (М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва)- 2 издание.-М.: Просвещение ,2009.
3. Сайты: www.edu.ru; www.shool.edu.ru; www.ege.edu.ru;
www. Center.fio.ru/method/getblob.asp?id=10000768 – разработки нетрадиционных уроков.
Слайд 5Задачи урока
Предметные: добиться усвоения учащимися систематических, осознанных сведений о логарифме;
формировать навыки использования свойств логарифмов при решении задач.
Метапредметные: развивать познавательный
интерес у учащихся через раскрытие практической необходимости и теоретической значимости темы и использование возможности ИКТ в изучении темы, умение находить творческий подход к решению разнообразных задач, продолжить формирование математической речи.Личностные: формирование представлений о математике как части общечеловеческой культуры, понимание значимости математики для общественного прогресса; воспитание познавательной активности, чувство ответственности, культуры общения, способствовать умению работать в коллективе и в команде, создать условия для развития у учащихся умений ставить проблемы и предлагать пути их решения;
Слайд 6Методы обучения:
частично-поисковый, исследовательский
Педагогические технологии:
личностно-ориентированное обучение, проектный метод.
Форма работы:
фронтальная, индивидуальная, групповая
Слайд 7Оснащение урока:
Мультимедийный проектор
Маркерная доска
Презентации, подготовленные учителем и учащимися
Подборка разноуровневых упражнений
для совершенствования навыков вычисления логарифмов, решения логарифмических уравнений и неравенств
Слайд 8 Ход урока:
Организационный момент
Вступительное слово учителя
Представление лабораторий и их
проблем
Работа в лаборатории и отчет о проделанной работе каждой лаборатории
Домашнее
заданиеРефлексия
Слайд 9Логарифмы
Холодные числа, внешне сухие формул математики полны внутренней
красоты и жара сконцентрированной в них мысли.
Александров А.Д.Слайд 10
В чем проявляется взаимосвязь развития математической науки и развития общества?
Математические
расчеты помогают
делать открытия;
Математика помогает вычислять
стоимость
покупки;Математические формулы помогут
рассчитать площадь комнаты;
Логарифмические формулы облегчат
вычисления степеней.
Слайд 11Значимость логарифмов
«С точки зрения вычислительной практики, изобретение логарифмов по
важности можно смело поставить рядом с другим, более древним великим
изобретением индусов – нашей десятичной системой нумерации.»Успенский Я. В.,
русский математик
Слайд 12Из истории логарифмов
Слово логарифм происходит от греческого λογοφ
(число) и ρίνμοφ (отношение) и переводится, следовательно, как отношение чисел.
Выбор изобретателем (1594 г.) логарифмов Джоном Непером такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое – геометрической.Слайд 15Логарифмом положительного числа b по основанию a, где a>0,
a≠1, называется показатель степени, в которую нужно возвести а чтобы
получить b.Пример:
Слайд 16В зависимости от значения основания приняты два обозначения
Если основанием является
10, то вместо log10 x пишут
lg x.2. Для введения следующего определения стоит понимать что за число e. Число е есть предел, к которому стремится при неограниченном возрастании n. Т.е Вместо loge x принято писать ln x.
Слайд 181. Логарифм произведения равен сумме логарифмов множителей:
2. Логарифм частного равен
разности логарифмов :
Слайд 193. Логарифм степени равен произведению показателя степени на логарифм ее
основания:
4. Логарифм корня равен отношению логарифма подкоренного выражения и показателя
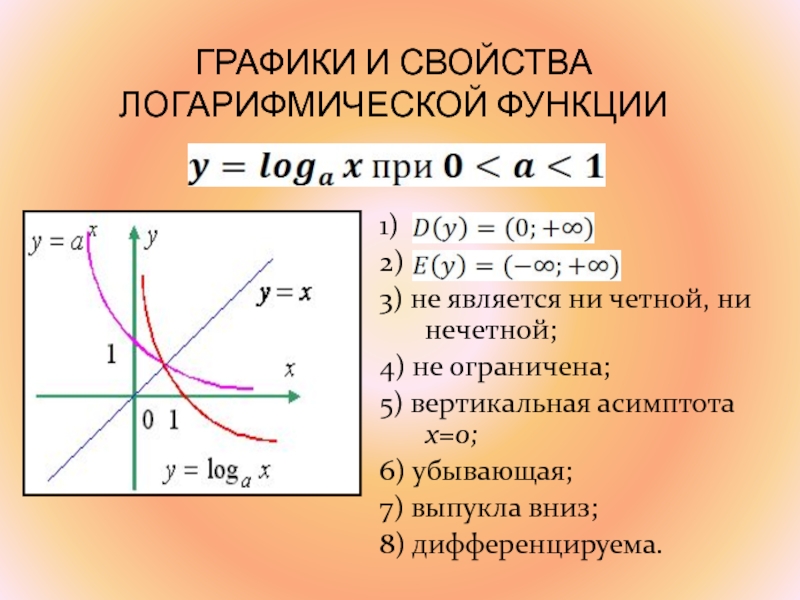
корня:Слайд 24ГРАФИКИ И СВОЙСТВА ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ
1)
;
2)
;3) не является ни четной, ни нечетной;
4) не ограничена;
5) вертикальная асимптота x=0;
6) убывающая;
7) выпукла вниз;
8) дифференцируема.
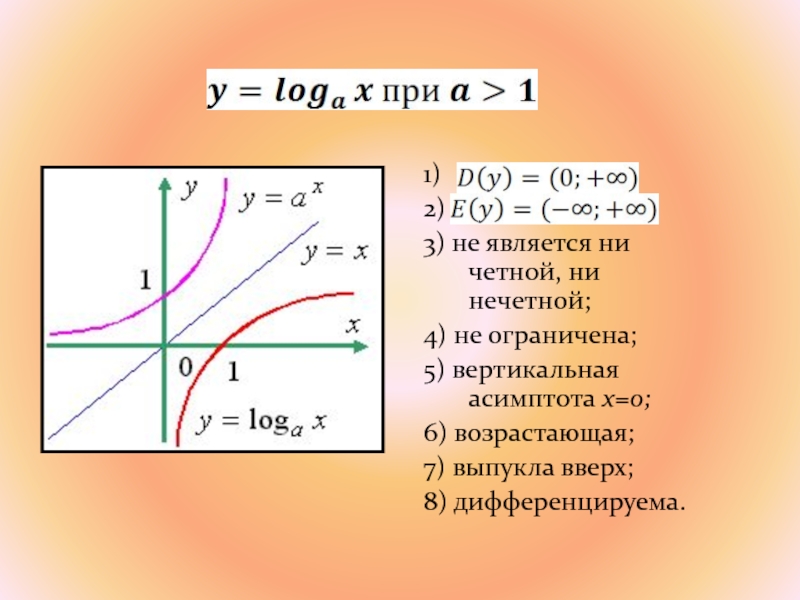
Слайд 251)
2)
3) не является ни четной, ни нечетной;
4) не ограничена;
5) вертикальная асимптота x=0;
6) возрастающая;
7) выпукла вверх;
8) дифференцируема.
Слайд 26Свойства функции:
Область определения (0; ∞)
Область значений R
Чётность /нечётность: функция не
является ни четной, ни нечетной
Нули функции: y = 0 при
x = 1Промежутки знакопостоянства: если 0 < a < 1, то y >0 при x € (0; 1), y < 0 при x € (1; ∞), если a > 1, то y >0 при x € (1; ∞), y < 0 при x € (0; 1)
Промежутки монотонности : при 0 < a < 1 функция убывает при x € (0; ∞) при a > 1 функция возрастает при x € (0; ∞)
Экстремумов нет.
График функции проходит через точку: (1; 0)
Асимптота x = 0
Слайд 27Применение логарифмической функции
Логарифмическая функция крайне важна в экономике, физике, при
проведении научных, экспериментальных расчетов, астрономии и др. Форма логарифмической спирали
присуща многим природным объектам.Физика — интенсивность звука (децибелы).
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.
Слайд 29РЕШИТЕ ПРИМЕРЫ, ОСНОВЫВАЯСЬ НА СВОЙСТВА ЛОГАРИФМА. ПРИ ОТВЕТЕ ПРОГОВОРИТЕ ЭТИ
СВОЙСТВА
Найдите области определения функций:
Слайд 30НА ОДНОМ ИЗ РИСУНКОВ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ У=LOG2Х. УКАЖИТЕ НОМЕР
ЭТОГО РИСУНКА.
Ответ: №4
Слайд 32ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
Уравнения, содержащие переменную под знаком логарифма
называются
логарифмическими.Простейшим примером логарифмического уравнения служит уравнение
loga х = b (где а > 0, а ≠1).
Его решение x = ab.
Слайд 33МЕТОДЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ
Функционально-графический
С использованием определения
Потенцирование
Введение новой переменной
Логарифмирование обеих
частей уравнения, если они положительны
Слайд 34ЗАПОМНИ !
Сладкая парочка!
Два в одном!
Два берега у одной реки!
Два сапога
– пара!
Близки и неразлучны!
Нам не жить
друг без
друга!
Логарифм и
ОДЗ вместе
трудятся
везде!
ОН
- ЛОГАРИФМ!
ОНА
-
ОДЗ!
Слайд 40Работа у доски с проверкой
Решение:
По определению логарифма:
4+x=52
4+x=25
x=21
Ответ:
x = 21.
Решение:
По определению логарифма:
8+x=2 3
8+x=8
x=0
Ответ: x
= 0.Слайд 41Работа у доски
с проверкой
Решение:
По определению логарифма:
9+x=34
9+x=81
x=72
Ответ: x
= 72.
Решение:
По определению логарифма:
3+x=27
3+x=128
x=125
Ответ: x = 125.
Слайд 44Логарифмическим неравенством называют неравенства вида
logaf(x) > logag(x),
где
а- положительное число, отличное от 1.
При а>1 logaf(x) > logag(x)
и f(x)>0, g(x) >0,то f(x)>g(x)
При 0 < а < 1 logaf(x) > logag(x) и
f(x)>0, g(x) > 0, то f(x) < g(x)
Слайд 45При решении логарифмических неравенств следует учитывать общие свойства неравенств, свойство
монотонности логарифмической функции и область её определения.
Слайд 50Работа у доски
Решение неравенств
log3 (2х-4)>log3(14-x)
Log1/3(2х-4)>log1/3(14-x)
6
Слайд 52Логарифмы в деятельности человека
в животноводстве
в астрономии
в экономике
в электротехнике
в музыке
в технике
Слайд 54Логарифмическая спираль – единственный тип спирали, не меняющей своей формы
при увеличении размеров. Видимо, это свойство и послужило причиной того,
что в живой природе логариф-мическая спираль встречается чаще других.Ночные бабочки, которые пролетают большие расстояния, ориентируясь по параллельным лунным лучам, инстинктивно сохраняют постоянный угол между направлением полета и лучом света.
Если они ориентируются на
точечный источник света,
инстинкт их подводит, и ба-
бочки попадают в пламя по
скручивающейся логариф-
мической спирали.
Слайд 56Рога животных растут лишь с одного конца. Этот рост осуществляется
по логарифмической спирали. Например, рога баранов, коз, антилоп и других
рогатых животных.Слайд 57Также происходит рост раковин морских животных . Поэтому раковины многих
моллюсков, улиток, закручены по логарифмической спирали.
Слайд 59По логарифмическим спиралям закручены и многие галактики, в частности –
Галактика Солнечной системы.
Слайд 60Логарифмы в музыке
«… Даже изящные искусства питаются ею
Набор передовых логарифмов?»
Из «Оды экспоненте»
Слайд 61 Музыканты редко увлекаются математикой, но
соприкасаются с
математикой гораздо чаще, чем сами подозревают. Известный физик Эйхенвальд вспоминал:«Представьте
же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах…»Слайд 62 Номера клавишей рояля представляют собой лога-рифмы чисел колебаний соответствующих звуков.
Слайд 63Логарифмы в живописи
Логарифмические линии в природе замечают не
только математики, но и художники. О копии картины Вермера «Кружевница»
Сальвадор Дали писал: я инстинктивно провелна холсте строгие
логарифмические кривые…»
Слайд 64“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия
- пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело –
совершенствовать материальную сторону жизни людей,а математика способна достичь всех этих целей”.
« Морис Клайн.»
Слайд 70Решить неравенства.
log 7 (3x - 9) < log 7 (x
+ 1)
log 1/3 (x + 6) > -2
log 1/2
(x - 5) + log 1/2 (x + 2) > -3 lg2 x - lg x - 20 >0
Слайд 71log 7 (3x - 9) < log 7 (x +
1)
Ответ. 3 < x < 5. н
log 1/2
(x - 5) + log 1/2 (x + 2) > -3 Ответ. 5< x < 6. е
log 1/3 (x + 6) > -2
Ответ. - 6 < x < 3. п
lg2 x - lg x - 20 > 0
Ответ. x >100000. р














 0, a≠1, называется" alt="Логарифмом положительного числа b по основанию a, где a>0, a≠1, называется показатель степени, в которую нужно">
0, a≠1, называется" alt="Логарифмом положительного числа b по основанию a, где a>0, a≠1, называется показатель степени, в которую нужно">
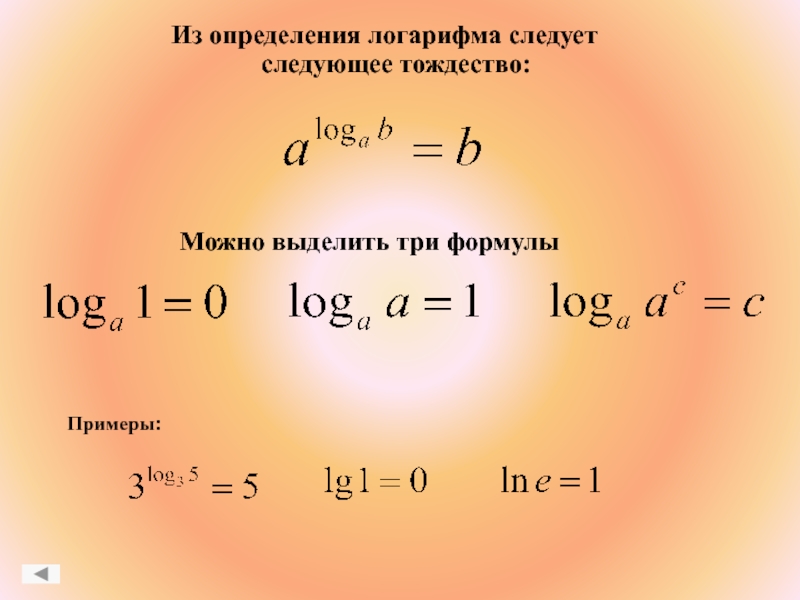
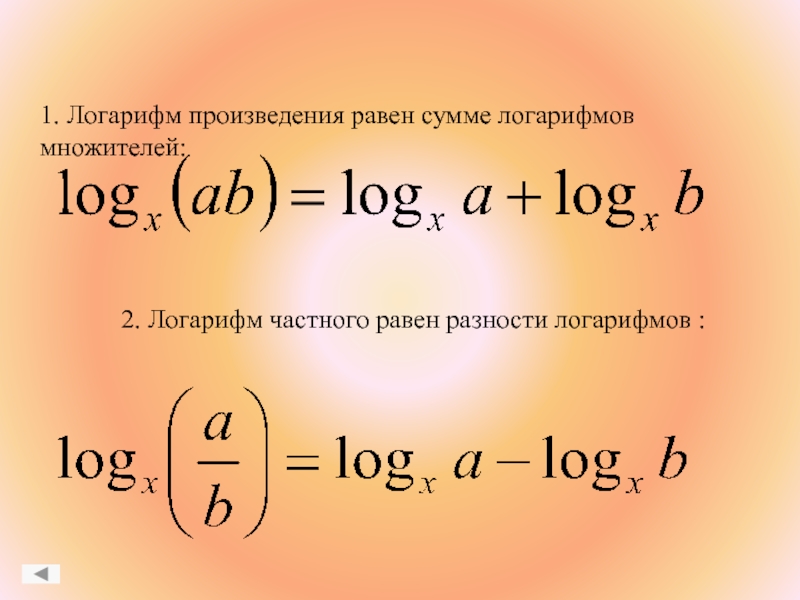
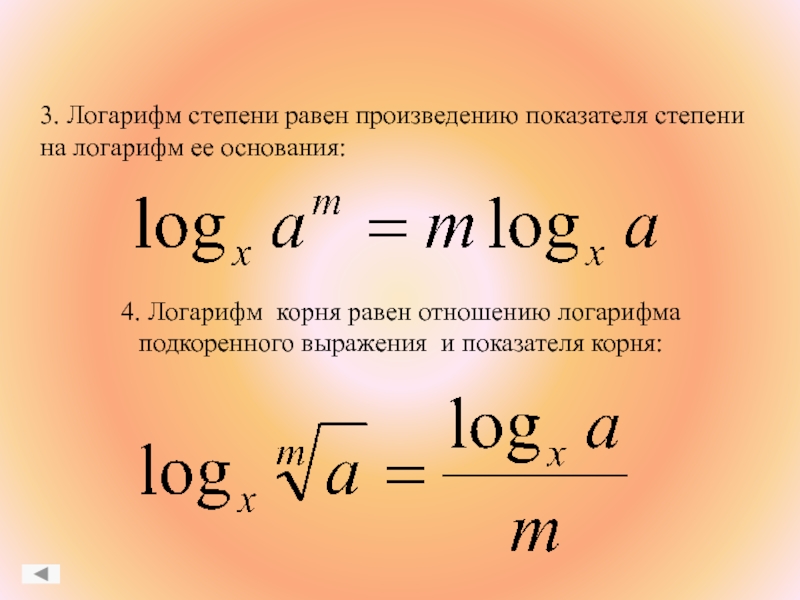
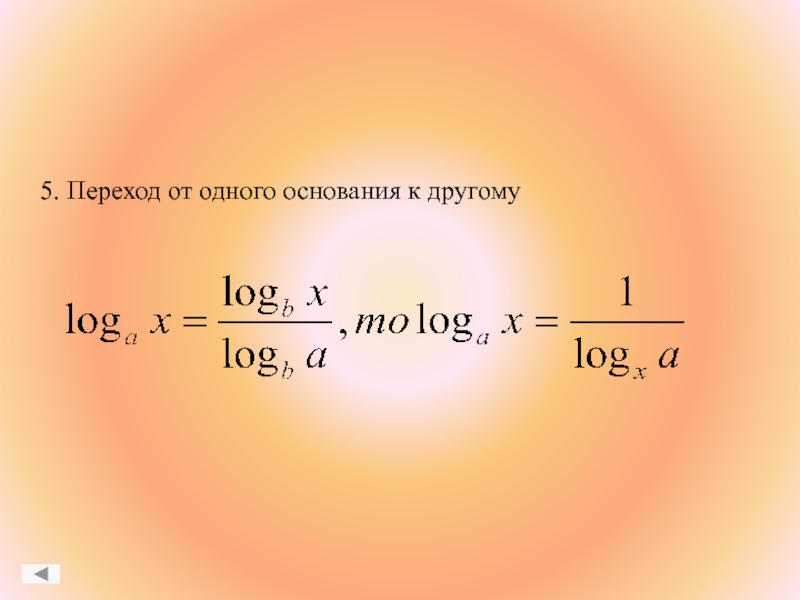

















 logag(x), где а- положительное" alt="Логарифмическим неравенством называют неравенства вида logaf(x) > logag(x), где а- положительное число, отличное от 1.При а>1 logaf(x)">
logag(x), где а- положительное" alt="Логарифмическим неравенством называют неравенства вида logaf(x) > logag(x), где а- положительное число, отличное от 1.При а>1 logaf(x)">




 log3(14-x)Log1/3(2х-4)>log1/3(14-x)6" alt="Работа у доски Решение неравенств log3 (2х-4)>log3(14-x)Log1/3(2х-4)>log1/3(14-x)6">
log3(14-x)Log1/3(2х-4)>log1/3(14-x)6" alt="Работа у доски Решение неравенств log3 (2х-4)>log3(14-x)Log1/3(2х-4)>log1/3(14-x)6">