Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме Иррациональные уравнения
Содержание
- 1. Презентация по теме Иррациональные уравнения
- 2. «Мне приходится делить время между политикой и
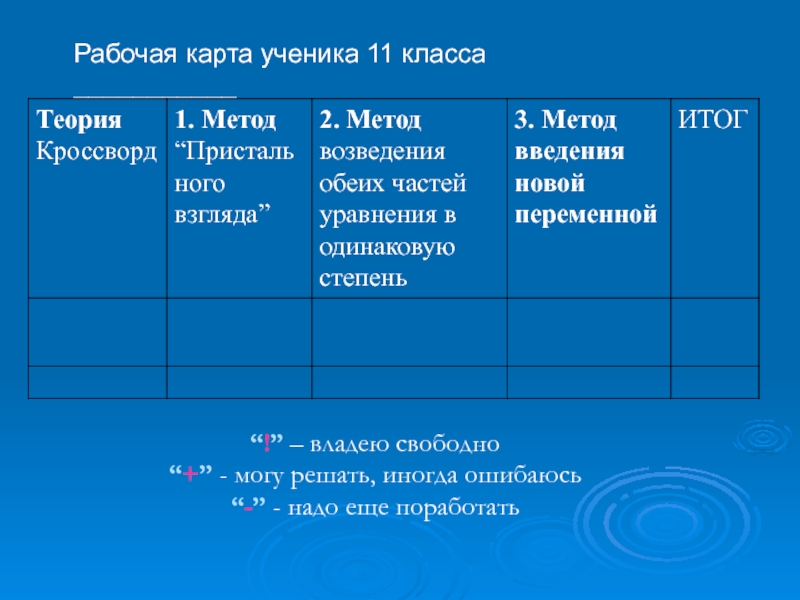
- 3. Рабочая карта ученика 11 класса ___________“!” –
- 4. «Иррациональное» в переводе с греческого: “Уму непостижимое,
- 5. Древнегреческий ученый-исследователь, который впервые доказал существование иррациональных чисел
- 6. 1. Какой этап является обязательным при решении
- 7. Е В К Л И ДПознание мира ведет к совершенствованию души.
- 8. Кто впервые ввёл изображение корня?
- 9. 1.Сколько решений имеет уравнение х2=0. 2.Корень какой
- 10. Кто ввел современное изображение корня?
- 11. 1.Как называется равенство двух алгебраических выражений? 2.Как
- 12. Назовите основные методы решения иррациональных уравнений
- 13. Метод возведения обеих частей уравнения в одинаковую степеньМетод «Пристального взгляда»Метод введения новой переменной
- 14. 1 группа2 группа3 группа
- 15. Свойства иррациональных выражений: А р и ф
- 16. Мажоранта и миноранта – (от франц.),
- 17. М – мажоранта.Если f(х) = g(х) и
- 18. Метод мажорант- Оценим левую часть- Оценим правую частьСоставим систему уравнений- Сделаем вывод- Проверка
- 19. Равноускоренное движение 1 и 2 космические
- 20. «Начала»Необходимость введения иррациональных чисел была описана в
- 21. Духовное самосовершенствованиеЧерты характера:трудолюбие, аккуратность, целеустремленность, терпениеТеорияМетоды решения
- 22. «Да, мир познания не гладок.И знаем мы со школьных летЗагадок больше, чем разгадокИ поискам предела нет!»
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2«Мне приходится делить время между политикой и уравнениями.
Однако, уравнения,
по – моему, гораздо важнее.
уравнения будут существовать вечно». ЭйнштейнСлайд 3Рабочая карта ученика 11 класса ___________
“!” – владею свободно
“+” -
могу решать, иногда ошибаюсь
“-” - надо еще поработать
Слайд 4«Иррациональное»
в переводе с греческого:
“Уму непостижимое,
неизмеримое,
немыслимое”
Открытие
иррациональности опровергало теорию
Пифагора о том, что
“всё
есть число”. 1
1
Слайд 5Древнегреческий ученый-
исследователь,
который впервые доказал
существование иррациональных
чисел
Слайд 61. Какой этап является обязательным при решении иррациональных уравнений?
2.
Способ, с помощью которого выполняется проверка решения иррационального уравнения.
3.
Как называется знак корня?4. Сколько решений имеет уравнение х2=а, если а<0?
5. Как называются уравнения, в которых под знаком корня содержится переменная?
6. Как называется корень второй степени?
проверка
радикал
ноль
иррациональные
квадратный
подстановка
Слайд 91.Сколько решений имеет уравнение х2=0.
2.Корень какой степени существует из
любого числа?
3.Как называется корень третьей степени?
4.Сколько решений имеет уравнение
х2=а, если а >0? 5.Как называется корень уравнения, который получается в результате неравносильных преобразований?
6.Корень какой степени существует только из неотрицательного числа?
одно
нечётной
кубический
два
посторонний
чётной
Слайд 111.Как называется равенство двух алгебраических выражений?
2.Как называют значение переменной,
при котором уравнение обращается в верное числовое равенство?
3.Какая черта
личности поможет при решении иррациональных уравнений? 4.Какой должен быть взгляд на уравнения, чтобы не вычисляя, назвать ответ?
5.Как называются уравнения, если они имеют одни и те же корни?
6.Как называется иррациональное выражение, содержащее противоположное арифметическое действие?
уравнение
корень
трудолюбие
пристальный
равносильные
сопряженное
Слайд 13
Метод возведения обеих частей уравнения в одинаковую степень
Метод «Пристального взгляда»
Метод
введения новой переменной
Слайд 15Свойства иррациональных выражений:
А р и ф м е т
и ч е с к и й корень четной степени
есть величина неотрицательная.Сумма, частное, произведение таких выражений будут также неотрицательны.
Арифметический корень четной степени существует только из неотрицательного числа.
Слайд 16 Мажоранта и миноранта –
(от франц.),
две функции, значение
первой из которых не меньше,
а второй не больше соответствующих
значений данной функции.Мажорирование – нахождение точек ограничения функции (словарь).
Метод мажорант – метод оценки левой и правой части уравнения.
Слайд 18 Метод мажорант
- Оценим левую часть
- Оценим правую часть
Составим
систему
уравнений
- Сделаем вывод
- Проверка
Слайд 19
Равноускоренное движение
1 и 2 космические скорости
Среднее значение
скорости теплового движения молекул
Период радиоактивного полураспада и другие.
А
также иррациональные уравнения использует статистика. Применение иррациональных уравнений