Слайд 1Презентация к уроку алгебры в 7 классе
по теме: «Определение степени
с натуральным показателем»
Выполнила
Яковлева В.Н.
учитель математики
первой квалификационной категории
МБОУ
«Карповская основная школа» муниципального образования - Ершичский район Смоленской области
2017 год
Слайд 2
Определение степени с натуральным показателем
Цели:
развить навыки возведения в степень;
научить находить значение выражений, содержащих степени с помощью калькулятора, используя
компьютер;
формировать приёмы умственного мышления как обобщение, классификация, абстрагирование;
воспитание интереса к математике решением задач на материале истории и культуры родного края
Слайд 3Ход урока
Самоопределение к деятельности
Актуализация знаний
Историческая справка
Групповая работа
Создание условий для постановки
учебной задачи
Открытие учащимися нового знания
Первичное закрепление
Включение в систему знаний
Самостоятельная работа
Творческие
задания
Итог урока
Домашнее задание
Слайд 4Жизнь украшается двумя вещами: занятием математикой и её преподаванием.
(Пуассон С.Д.)
Если хочешь строить мост,
Наблюдать движенье звёзд,
Управлять машиной в
поле
Иль вести машину ввысь,
Хорошо работай в школе,
Добросовестно учись.
(М. Бозаковский)
Слайд 5Проверка домашнего задания
1. Дать определение степени числа а с натуральным
показателем п, большим 1.
2.Что называется степенью числа а с натуральным
показателем 1?
3. Каким числом является степень отрицательного числа с чётным показателем?
4. Каким числом является степень отрицательного числа с нечётным показателем?
Слайд 6Устная работа
1.Найти а2; 2а2; (-а)2; -а2, если а=0,5.
2. Определить знак
степени: (-2)7; (-8)4; (-5)6; (-10)9.
3. Вычислить: (4∙2)2-4∙22.
4. Вычислить, используя таблицу
квадратов на форзаце учебника:
352-3; 712+1; 272-10; 432+12.
Слайд 7Историческая справка
Первое упоминание о Смоленске было в 863 году, и
уже тогда он был «велик и мног людьми». Смоленск -
город ключ и носит гордое звание города героя. Давайте решим задачу связанную с нашим прекрасным городом.
Слайд 8В Смоленске множество памятников архитектуры
Слайд 9
Успенский собор – православный храм
Задача
Окно в православном храме имеет форму прямоугольника, завершающегося полукругом. Составить формулу для вычисления его площади S (в квадратных сантиметрах), если известно, что основание прямоугольника равно а см, высота прямоугольника в 3 раза больше основания.
Найти площадь окна, если а=80. (Указание. Площадь круга равна πr² , где r – радиус круга,
π ≈ 3,14.)
Слайд 10Групповая работа
Группа «Исследователи» составляют выражение для решения задачи.
Группа «Вычислители» находят
значение выражения 3а2+ πа2/8, если а=80
Слайд 11Проверка решения задачи
Решение.
S=3а2+ πа2/8, если а=80,
то S=3∙6400+3,14∙6400/8=19200+3,14∙800=
=19200+2512=21712(см2)
Слайд 12Проблема: 2,75
Укажите способы нахождения значения степени
Слайд 13Способы
1.Пользуясь правилом умножения десятичных дробей
2. Использовать таблицу квадратов: 7,29*7,29*2,7
3. Использовать
для вычислений калькулятор
Слайд 14Назовите тему урока
Определение степени с натуральным показателем
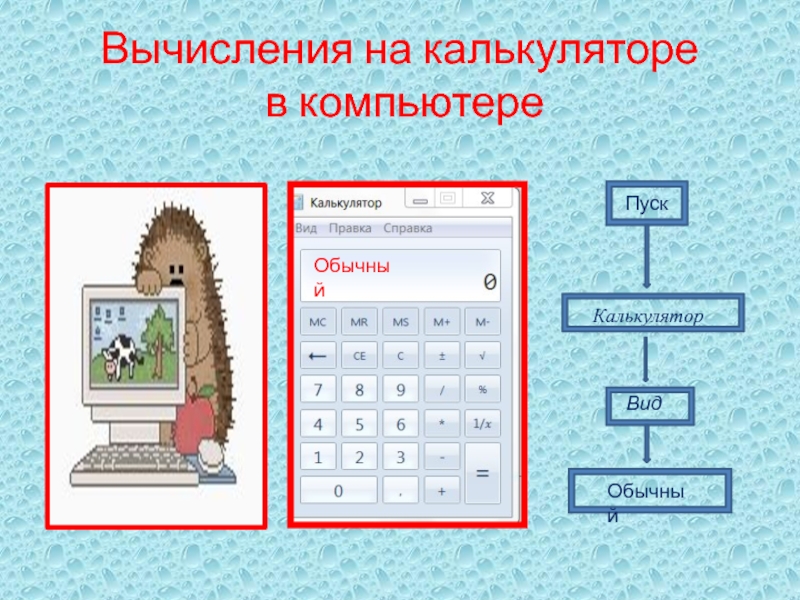
Слайд 15Вычисления на калькуляторе
в компьютере
Обычный
Калькулятор
Пуск
Вид
Обычный
Слайд 16Виды калькуляторов
3,2 4=104,8576
Инженерный
Слайд 18Работа по учебнику
Пример 3. Найти с помощью калькулятора значение степени
2,75.
Схема1.
2,7 x 2,7 х 2,7 х 2,7
х 2,7 = 143,48907;
Схема2.
2,7 х = = = = 143,48907
Вывод: более удобна схема 2.
Слайд 19Калькулятор в компьютере
Пуск
Калькулятор
378. Вычислить
с помощью калькулятора:
а) 4,153; в) 1,426; д) 1,674·8,3.
б) (-0,98)5; г) 2,083:1,56;
Ответы:
а) 71,473375; в) 8,198418170944;
б) -0,9039207968; г) 5,7685(3);
д) 64,557094643.
Слайд 20А сейчас вам предстоит выполнение самостоятельной работы
Используя калькулятор,
нужно заполнить таблицу.
Откройте, пожалуйста, страницу 90 вашего учебника.
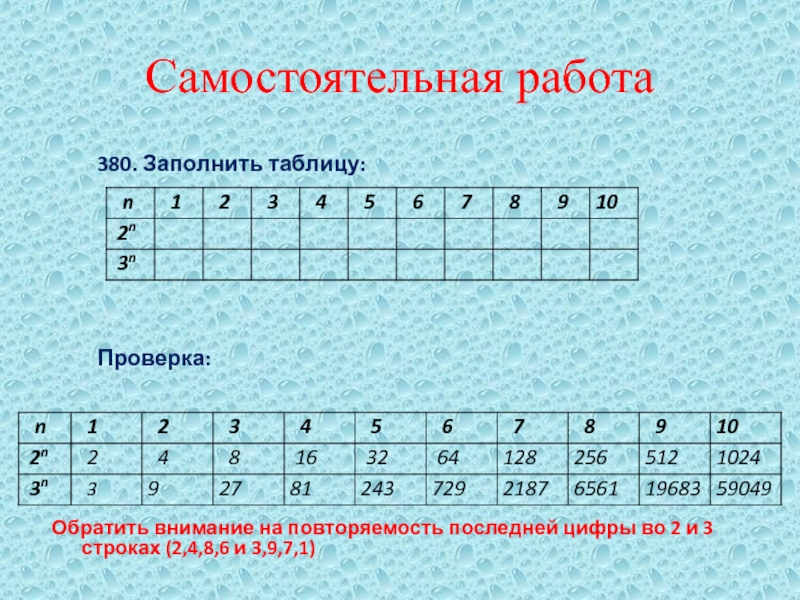
Слайд 21Самостоятельная работа
380. Заполнить таблицу:
Проверка:
Обратить внимание на повторяемость
последней цифры во 2 и 3 строках (2,4,8,6 и 3,9,7,1)
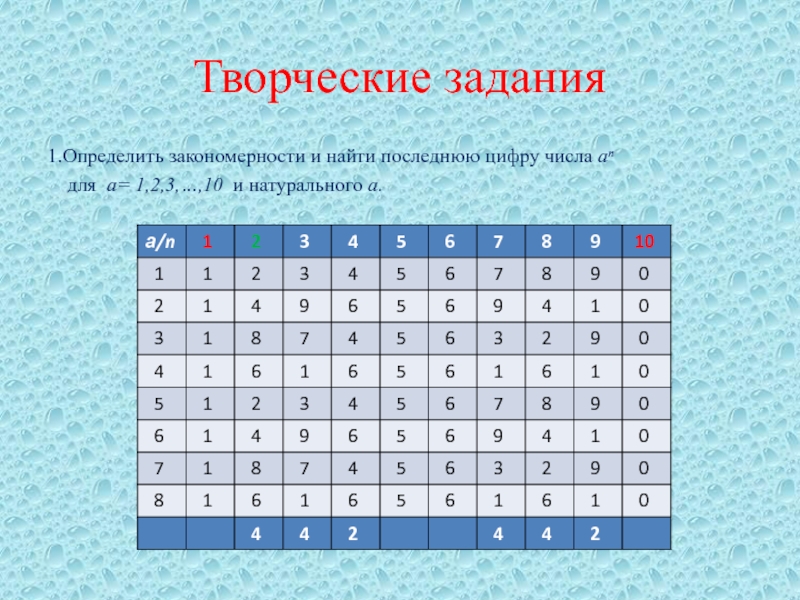
Слайд 22Творческие задания
1.Определить закономерности и найти последнюю цифру числа аⁿ
для а= 1,2,3,…,10 и натурального а.
Слайд 23Ответ:
Результаты указаны в таблице.
Сверху указано основание а,
слева
– степень n=1,2,3,…,8.
В последней строке указана повторяемость последней цифры.
Видно .что при возведении а=1;5;6;10 в любую степень последняя цифра не меняется.
При возведении а=2;3;7;8 последняя цифра повторяется при изменении показателя степени
на 4.
При возведении а=4;9 последняя цифра повторяется при изменении показателя степени на 2.
Слайд 24Устали?
Физкультминутка
Быстро встали, улыбнулись.
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо-влево
повернитесь,
Рук коленями коснитесь.
Сели-встали. Сели-встали.
И на месте побежали.
Слайд 25Творческие задания
2. Используя результаты предыдущей задачи (смотри таблицу), найти последнюю
цифру числа:
а) 20042004;
б) 1936537; в)58671993; г) 2435183;
д) 36481734.
Слайд 26Ответ:
а) 6 (последняя цифра основания 4, показатель степени 2004 кратен
4);
б) 6 (последняя цифра основания 6, число 6 в любой
степени оканчивается на 6);
в) 7 (последняя цифра основания 7, показатель 1993 при делении на 4 даёт остаток 1, то есть 1993=4∙498+1);
г) 5 (последняя цифра основания 5. Число 5 в любой степени оканчивается на 5);
д) 4 (последняя цифра основания 8, показатель степени 1734 при делении на 4 даёт остаток 2, то есть 1734=4∙433+2).
Слайд 27Рефлексия
1. Дать определение основания степени.
2.
Дать определение показателя степени.
3. Какое число получается
при возведении нуля в степень?
4. Какое число получается при возведении положительного числа в степень?
Отрицательного? От чего зависит результат?
5. Найти значение степени 3,2⁴ с помощью калькулятора.
3,2 х = = = 104,8576
Пуск Калькулятор
Слайд 28Домашнее задание
379. Найти с помощью калькулятора значение выражения.
390. Составить формулу
для вычисления площади кольца, если R=6,4 см, r=3,6 см.
r
R