окружности.
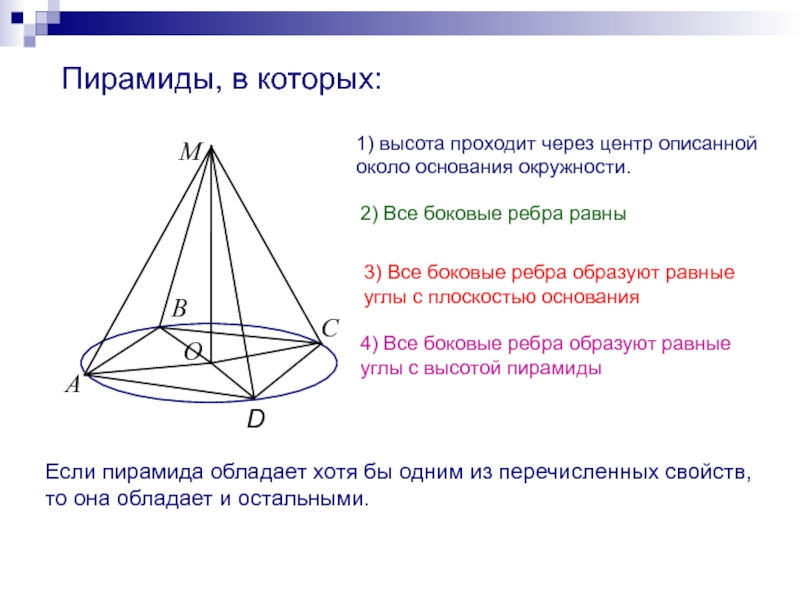
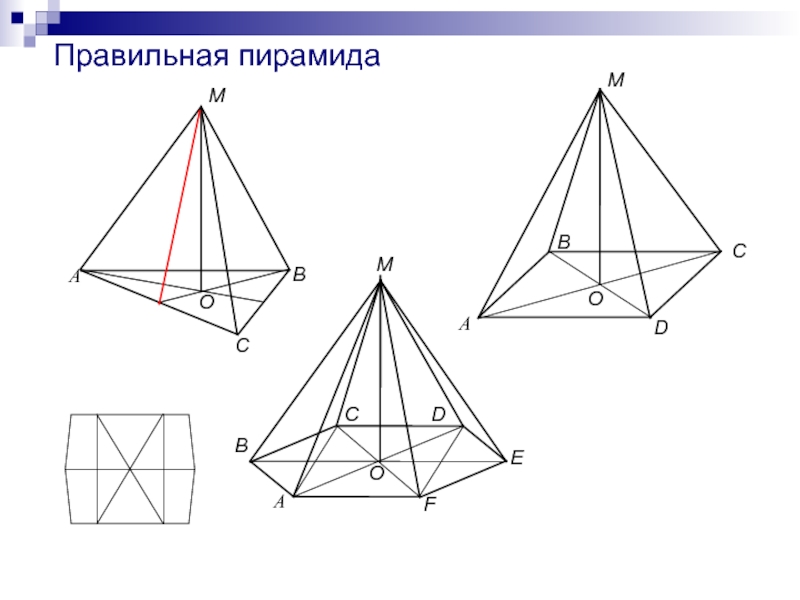
2) Все боковые ребра равны
3) Все боковые ребра образуют равные
углы с плоскостью основания4) Все боковые ребра образуют равные углы с высотой пирамиды
Если пирамида обладает хотя бы одним из перечисленных свойств, то она обладает и остальными.