Пирамида
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация темы: Пирамида
Презентация на тему Презентация на тему Презентация темы: Пирамида из раздела Математика. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 19 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
Слайды и текст этой презентации
А1
А2
Аn
Р
А3
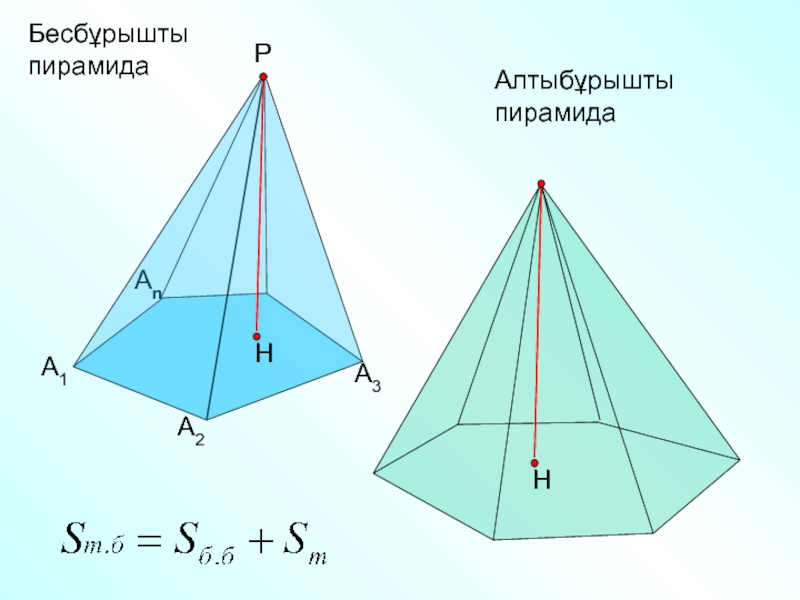
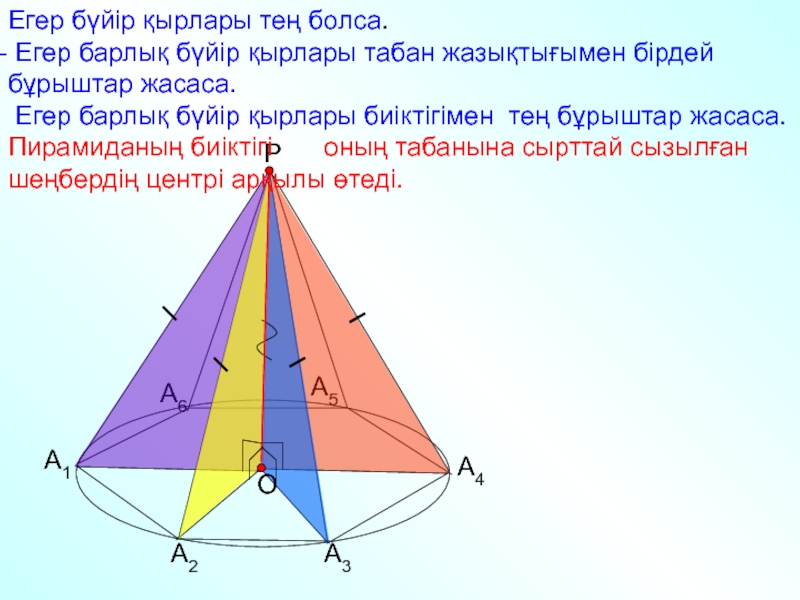
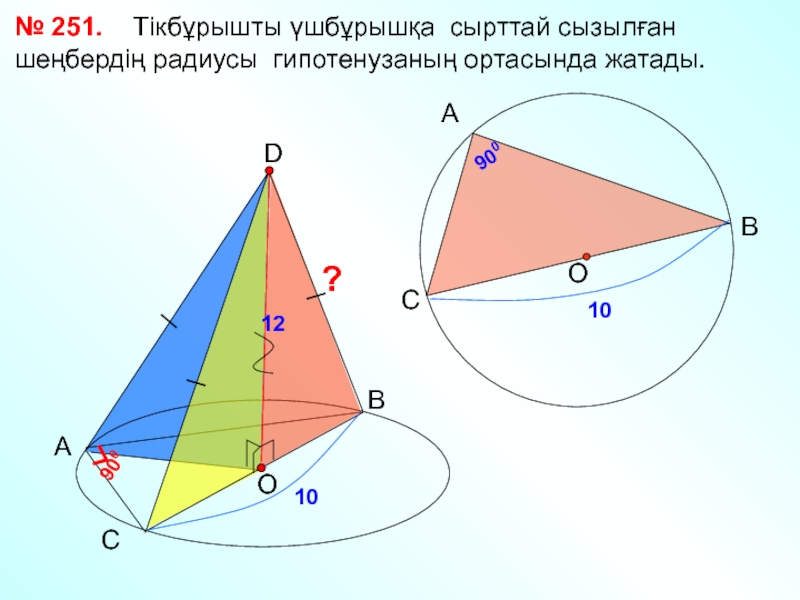
Пирамида деп бір жағы кез келген көпбұрыш ,ал қалған п жағы төбелері ортақ үшбұрыштардан тұратын көпжақты атайды..
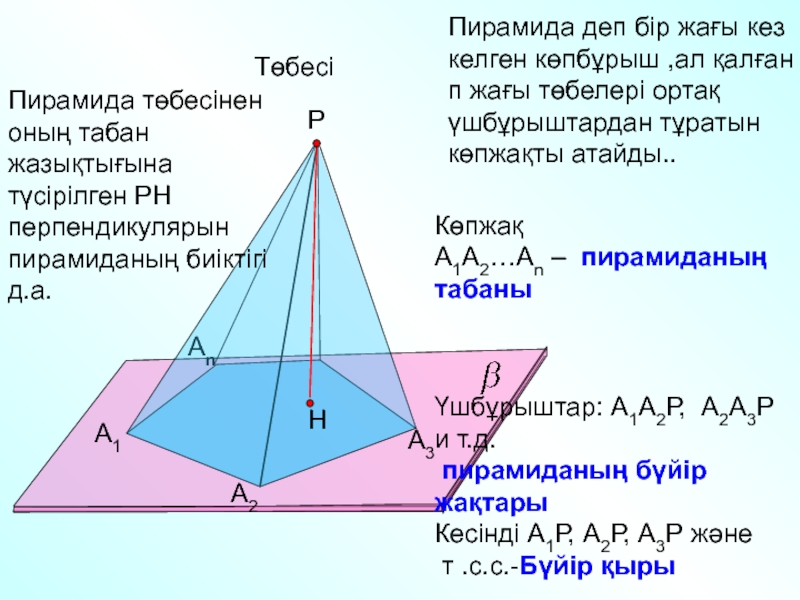
Төбесі
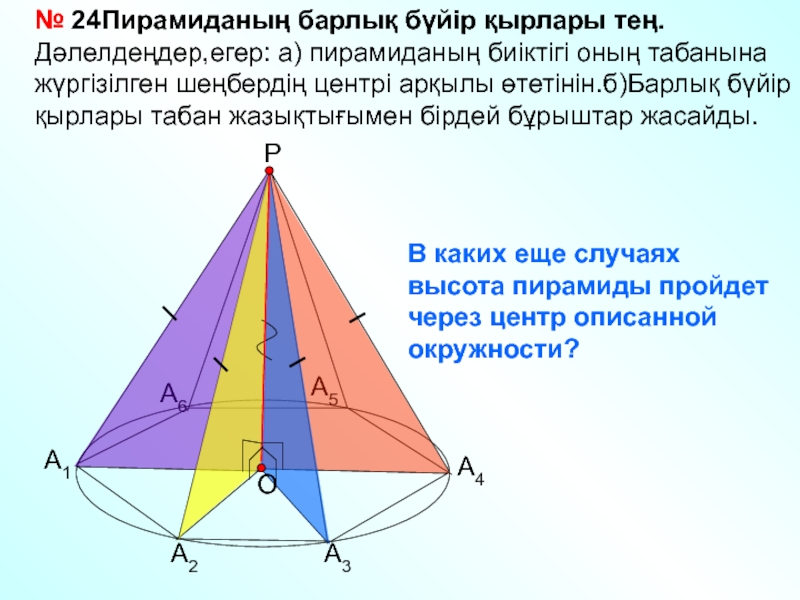
Пирамида төбесінен оның табан жазықтығына түсірілген РН перпендикулярын пирамиданың биіктігі д.а.
Көпжақ
А1А2…Аn – пирамиданың табаны
Үшбұрыштар: А1А2Р, А2А3Р и т.д.
пирамиданың бүйір жақтары
Кесінді А1Р, А2Р, А3Р және
т .с.с.-Бүйір қыры
Табаны дұрыс көпбұрыш болып төбесінің проекциясы табанының центріне дәл түссе оны дұрыс пирамида д.а..
Дұрыс көпбұрыштың центрі деп оған сырттай (іштей) сызылған шеңбердің центрін айтады.
Дұрыс пирамиданың бүйір жағының пирамида төбесінен түсірілген биіктігі пирамиданың апофемасы д.а.
А1
А2
А3
А4
А5
А6
Р
Дұрыс пирамиданың бүйір бетінің ауданы оның табанының жарты периметрі мен апофемасының көбейтіндісіне тең.
А1
А2
А3
А4
А5
А6
Р
Дұрыс пирамиданың барлық бүйір қырлары тең,ал бүйір жақтары тең болып келген теңбүйірлі үшбұрыштар екенін дәлелдейік.
А1
А2
А3
А4
А5
А6
Р
С
А
В
Н
№1Пирамиданың табаны қабырғасы 5см тең ромб,ал оның бір диагоналі 8 см. Бүйір қырын тап,егер оның биіктігі табанының диагоналдарының қилысу нүктесі арқылы өтсе және 7 см болса.
O
D
5 см
5 см
7
4
3
С
В
А
D
DАВС пирамиданың табаны АВС үшбұрышына тең, яғни мұндағы АВ = АС = 13 см, ВС = 10 см. АД бүйір қыры 9 см және табан жазықтығына перпендикуляр .Пирамиданың бүйір бетінің ауданын табыңдар.
№ 2.
13
9
10
13
С
В
А
D
Пирамиданың табаны тікбұрышты үшбұрыш АВС-ға тең.. АВ = 29 см, катет АС = 21 см. АД бүйір қыры 20 см және табан жазықтығына перпендикуляр болса Sб.б DАВС тап.
№3.
21
20
29
Пирамиданың табаны параллелограмм оның қабырғалары 20см және 36 см тең,ал ауданы 360 см2. Пирамиданың биіктігі табанының диагоналдарының қилысу нүктесі арқылы өтеді және 12 см-ге тең. Sт,б тап.
D
Н
O
А
B
№4.
С
20
36
12
№ 24Пирамиданың барлық бүйір қырлары тең. Дәлелдеңдер,егер: а) пирамиданың биіктігі оның табанына жүргізілген шеңбердің центрі арқылы өтетінін.б)Барлық бүйір қырлары табан жазықтығымен бірдей бұрыштар жасайды.
А1
А2
А3
А4
А5
А6
Р
В каких еще случаях высота пирамиды пройдет через центр описанной окружности?
А1
А2
А3
А4
А5
А6
Р
Егер бүйір қырлары тең болса.
Егер барлық бүйір қырлары табан жазықтығымен бірдей бұрыштар жасаса.
Егер барлық бүйір қырлары биіктігімен тең бұрыштар жасаса. Пирамиданың биіктігі оның табанына сырттай сызылған шеңбердің центрі арқылы өтеді.
№ 250.Пирамиданың табаны арасы 1200 болып келген теңбүйірлі үшбұрыш. Бүйір қырлары оның биіктігімен 450 бұрыш жасайды және биіктігі 16см.Табанының ауданын тап.
А
В
С
Р
1200
450
16
На чертеже ошибка!
№ 250.Доғал бұрышты үшбұрышқа сырттай сызылған шеңбердің радиусы оның сыртқы облысында жатады.
А
В
С
Р
1200
SАВС
А
№ 251. DABC пирамиданың табаны гипотенузасы ВС болатын тікбұрышты үшбұрыш.Бүйір қырлары бір-біріне тең,биіктігі 12 см.Егер ВС = 10 см болса бүйір қырларын тап.
В
С
D
900
На чертеже ошибка!
№ 251. Тікбұрышты үшбұрышқа сырттай сызылған шеңбердің радиусы гипотенузаның ортасында жатады.
А
В
С
D
900
10
