Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация Замечательные кривые
Содержание
- 1. Презентация Замечательные кривые
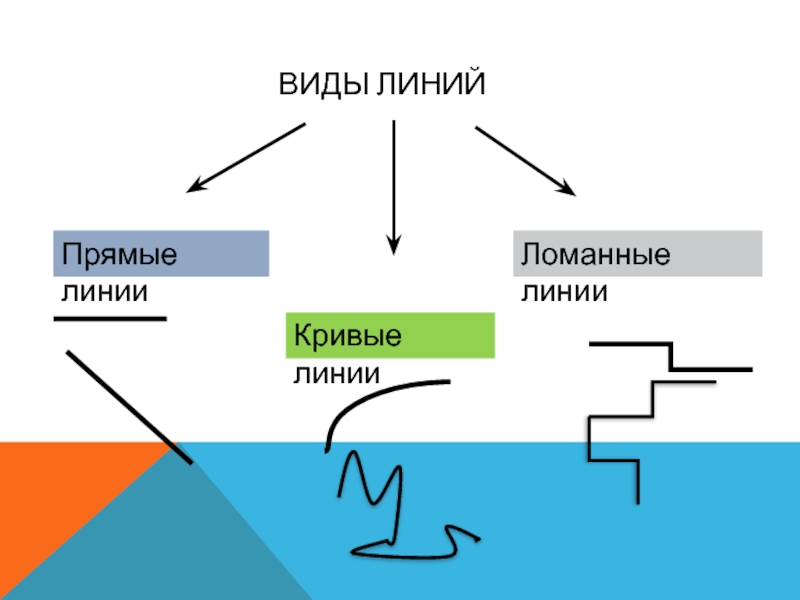
- 2. ВИДЫ ЛИНИЙПрямые линииКривые линииЛоманные линии
- 3. Слайд 3
- 4. Слайд 4
- 5. ЭЛЛИПС…Практика: на картоне поставьте две точки (фокусы)
- 6. ЭЛЛИПС?Итог и выводы: каким свойством обладают все
- 7. Слайд 7
- 8. ЗАДАЧАЭллипс: АС+СВ=26 см АD+BD
- 9. Слайд 9
- 10. О, ЭЛЛИПС (ИЗ ИСТОРИИ)
- 11. ЭЛЛИПС В ЖИЗНИ
- 12. ЭЛЛИПС В ЖИЗНИ
- 13. Закономерные кривые линииПознакомимся ещё с несколькими закономерными
- 14. Слайд 14
- 15. Слайд 15
- 16. ЗадачаГипербола: MB-AM=100 см. АТ - ? ТВ=24
- 17. Эту замечательную кривую можно встретить в повседневной
- 18. ПАРАБОЛА
- 19. ПАРАБОЛА
- 20. ПАРАБОЛА
- 21. ПАРАБОЛА
- 22. Слайд 22
- 23. Слайд 23
- 24. 1) Представьте, что конус разрезается плоскостью, параллельной основанию. Какая получится фигура на плоскости разреза (в сечении)?
- 25. 2) Представьте, что конус разрезается плоскостью под
- 26. 3) Представьте, что конус разрезается плоскостью,
- 27. 1. Круг (рис.А); 2. Эллипс (рис.Б); 3. Парабола (рис.В) и ветвь гиперболы (рис. Г)
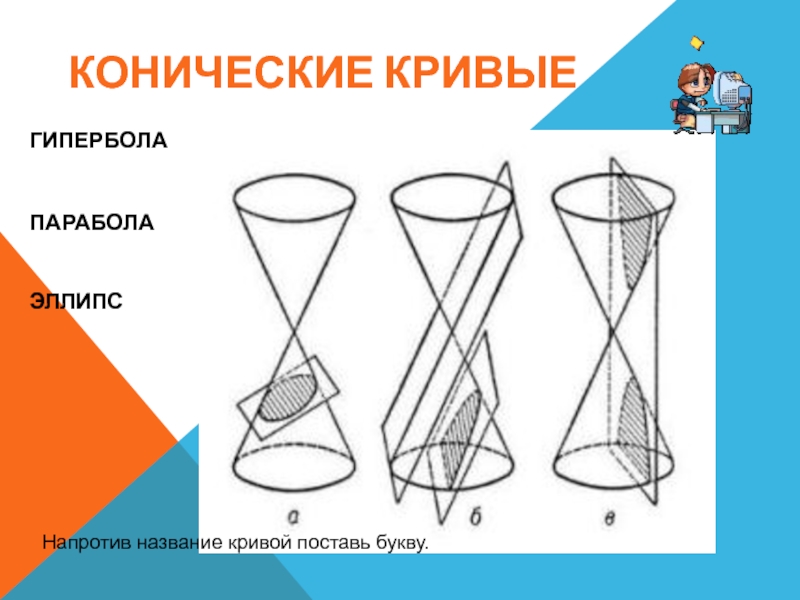
- 28. КОНИЧЕСКИЕ КРИВЫЕГИПЕРБОЛАПАРАБОЛАЭЛЛИПСНапротив название кривой поставь букву.
- 29. СПИРАЛЬ АРХИМЕДА
- 30. Спираль АрхимедаСлово «спираль» в переводе с латыни
- 31. Спираль Архимеда
- 32. Спираль Архимеда
- 33. Паук плетёт паутину по спирали.Головка подсолнуха состоит
- 34. Слайд 34
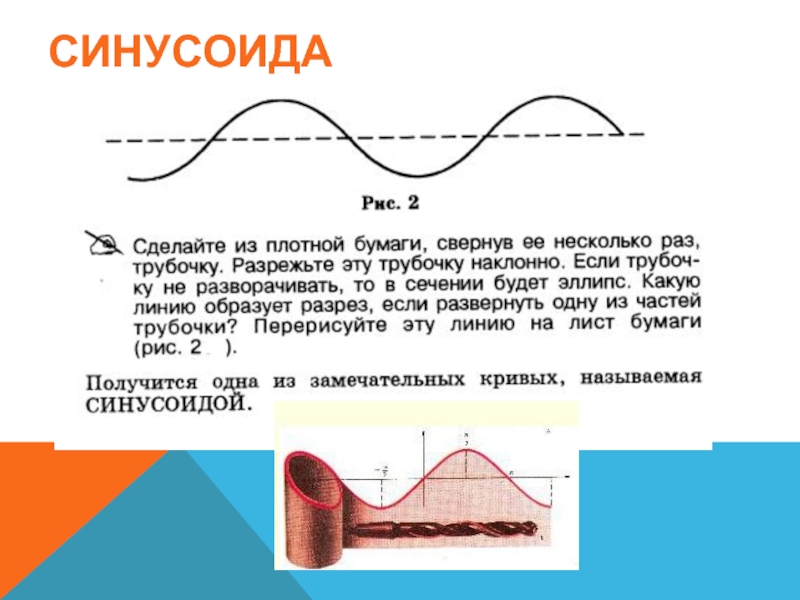
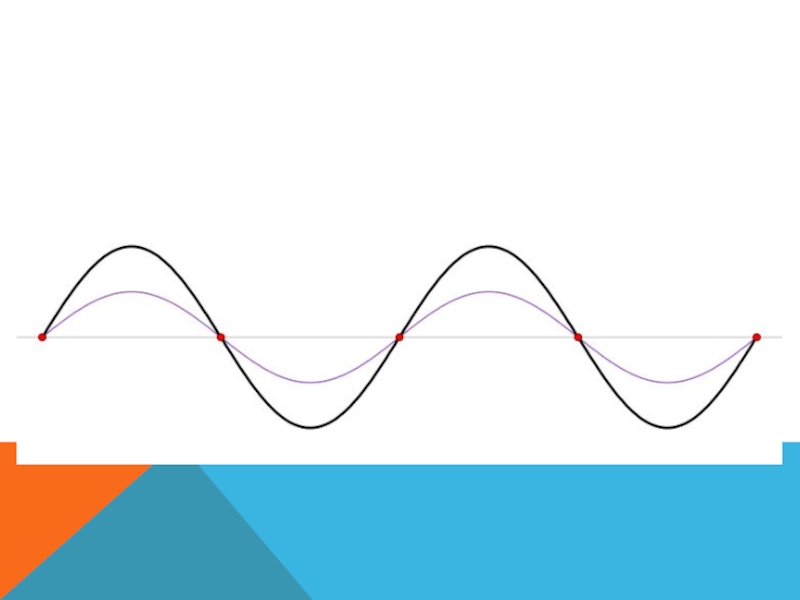
- 35. СИНУСОИДА
- 36. Слайд 36
- 37. МЫ все живем в пределах синусоиды.То на
- 38. СИНУСОИДА
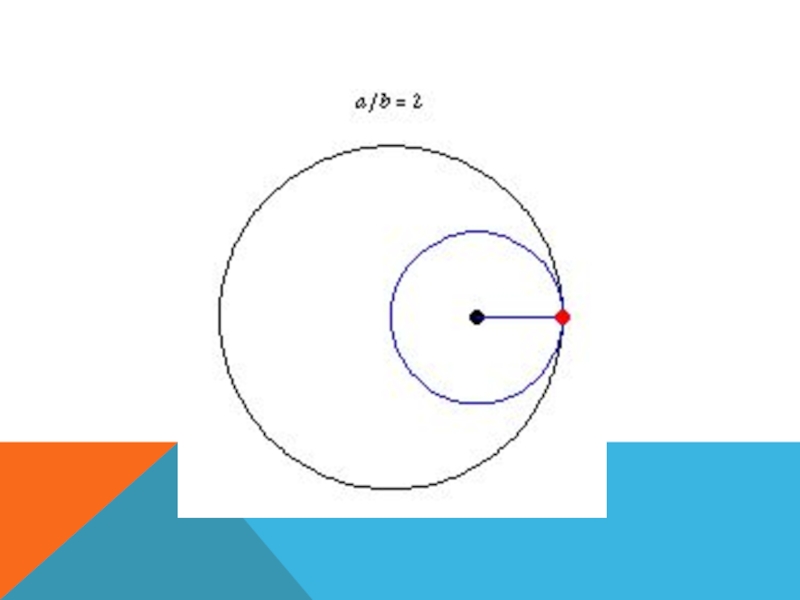
- 39. КАРДИОИДА …Практика (на компьютере):
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. ЭТО КАРДИОИДА. ТАКОЕ НАЗВАНИЕ ОНА ПОЛУЧИЛА ИЗ-ЗА
- 44. Слайд 44
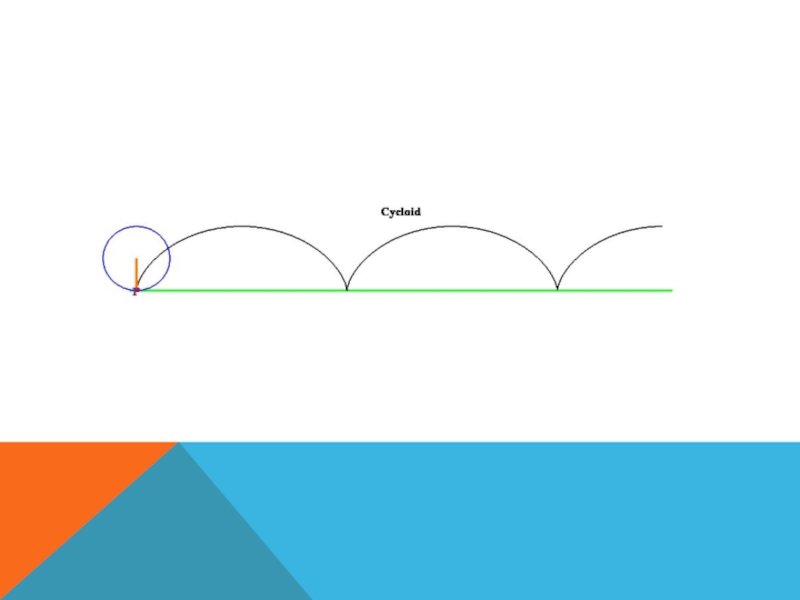
- 45. ЦИКЛОИДА …Практика (в Википедии компьютерная модель) :
- 46. Слайд 46
- 47. Слайд 47
- 48. - Прямолинейный желоб? - Итальянский ученый Галилео
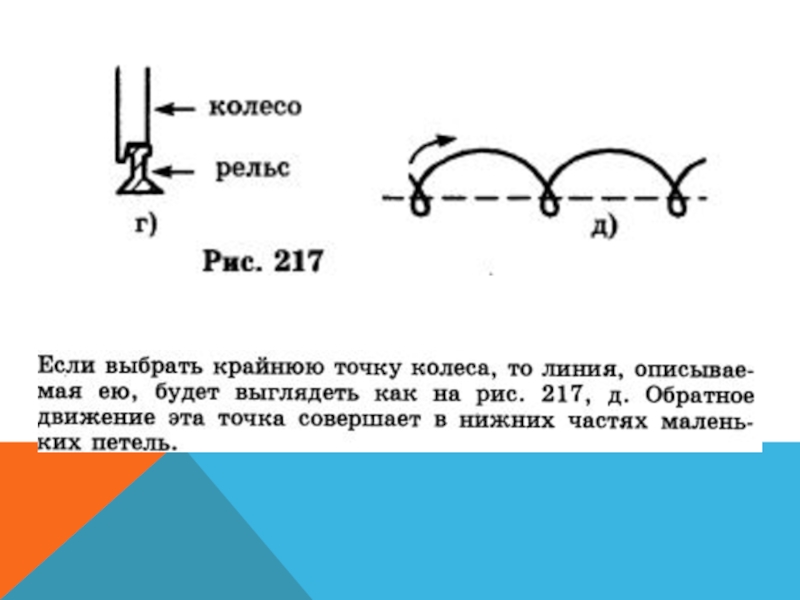
- 49. КАК ДВИЖУТСЯ КОЛЕСА ПОЕЗДА?
- 50. Слайд 50
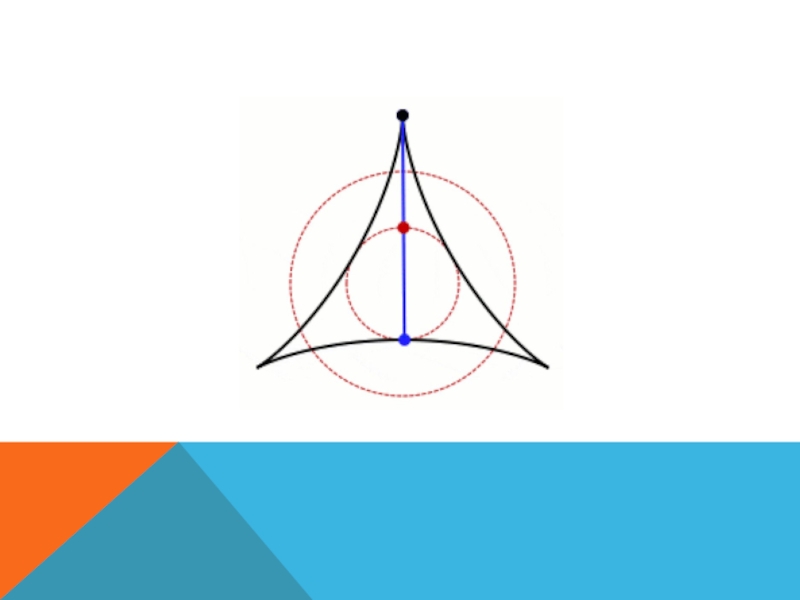
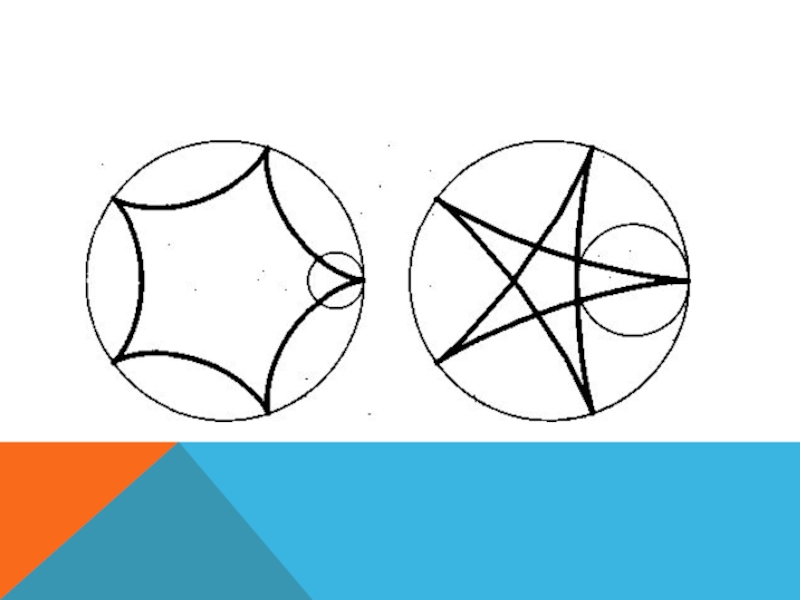
- 51. ГИПОЦИКЛОИДА …Практика (демонстрация на доске или в энциклопедии):
- 52. Слайд 52
- 53. ГИПОЦИКЛОИДА?Исследование:Итоги исследования: ________________________________________________________________________________________________________________________________________________________________________________________________
- 54. Слайд 54
- 55. Слайд 55
- 56. Слайд 56
- 57. Передо мной овал пруда, Я – с
- 58. Слайд 58
- 59. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1«ПОСТРОЕНИЕ ЗАМЕЧАТЕЛЬНЫХ КРИВЫХ»
Наглядная геометрия 6 класс
Эллипс. Гипербола. Парабола. Конус.
Спираль Архимеда
Ельца Караулова М.С.Слайд 5ЭЛЛИПС…
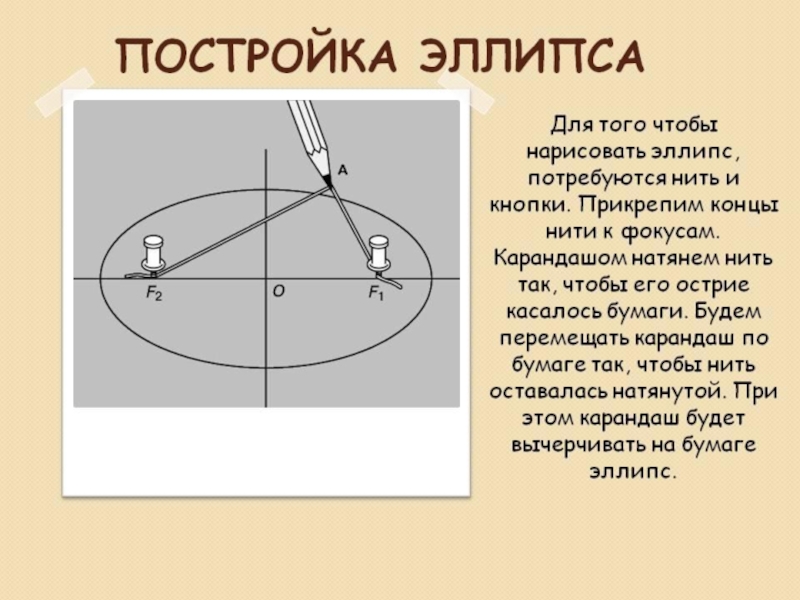
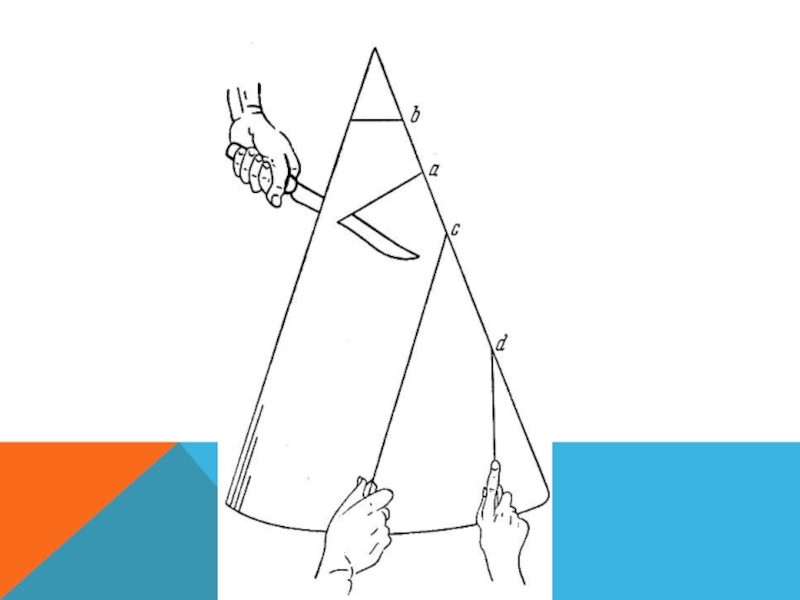
Практика: на картоне поставьте две точки (фокусы) и протяните через
них нитку. Натяните нитку карандашом и нарисуйте фигуру.
Исследование: что произойдет,
если 1 ряд фокусы приблизить друг к другу;
2 ряд фокусы удалить друг от друга;
3 ряд фокусы совместить?
Слайд 6ЭЛЛИПС?
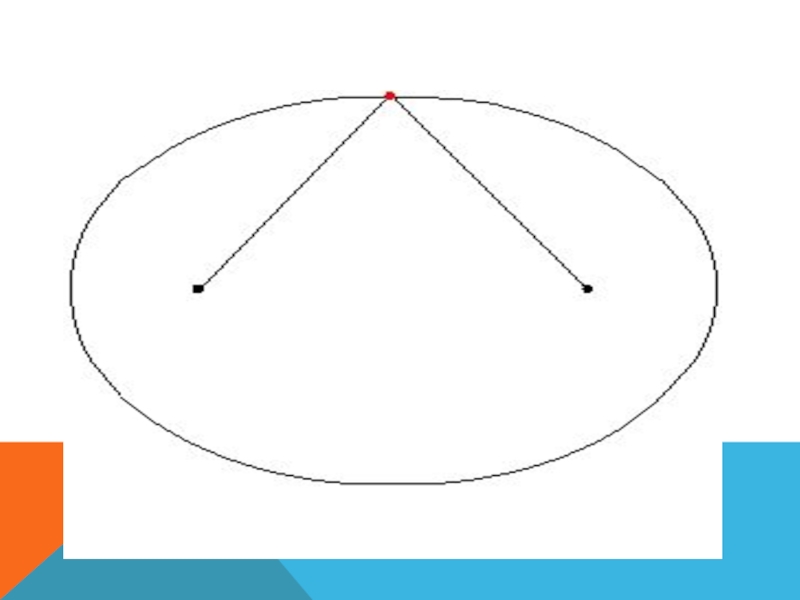
Итог и выводы: каким свойством обладают все точки эллипса (вспомните
как мы строили эту кривую).
Итак, сумма расстояний от любой точки
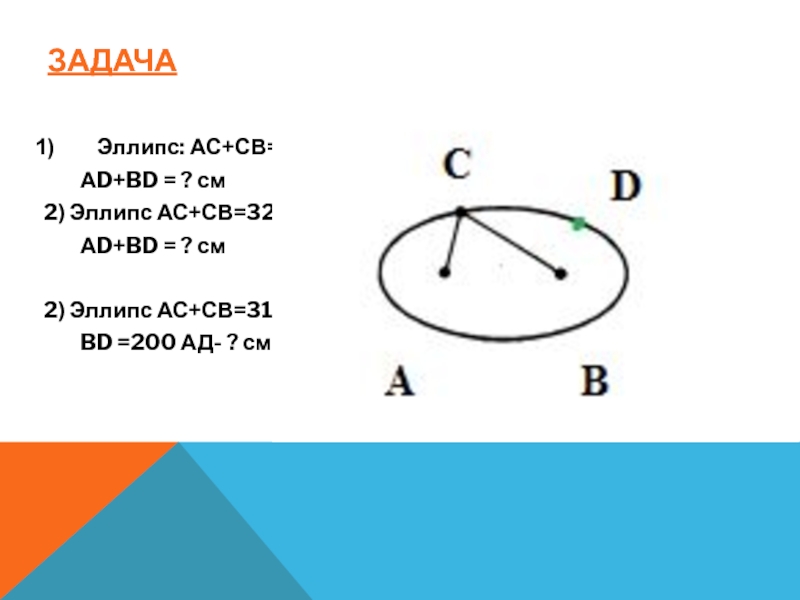
эллипса до двух точек плоскости (фокусов) есть величина постоянная. Окружность частный случай эллипса.Слайд 8ЗАДАЧА
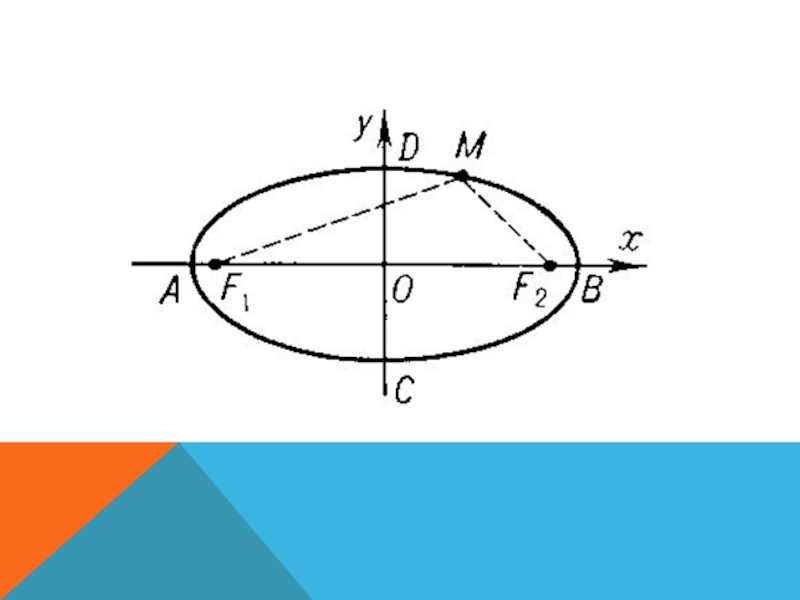
Эллипс: АС+СВ=26 см
АD+BD = ? см
2)
Эллипс АС+СВ=32 см
АD+BD = ? см
2)
Эллипс АС+СВ=310 смBD =200 АД- ? см
Слайд 13Закономерные кривые линии
Познакомимся ещё с несколькими закономерными кривыми линиями.
Гипербола.
Эта кривая,
так же как и эллипс, имеет два фокуса, но в
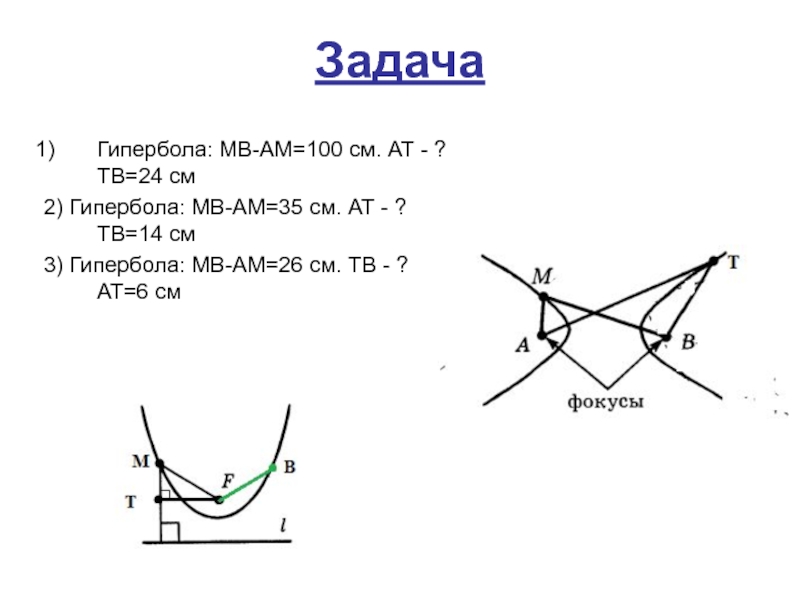
отличие от эллипса, гипербола состоит из двух отдельных ветвей. Основное свойство гиперболы: разность расстояний от любой точки гиперболы до двух её фокусов является постоянной величиной.Слайд 16Задача
Гипербола: MB-AM=100 см. АТ - ? ТВ=24 см
2) Гипербола: MB-AM=35
см. АТ - ? ТВ=14 см
3) Гипербола: MB-AM=26 см. ТВ
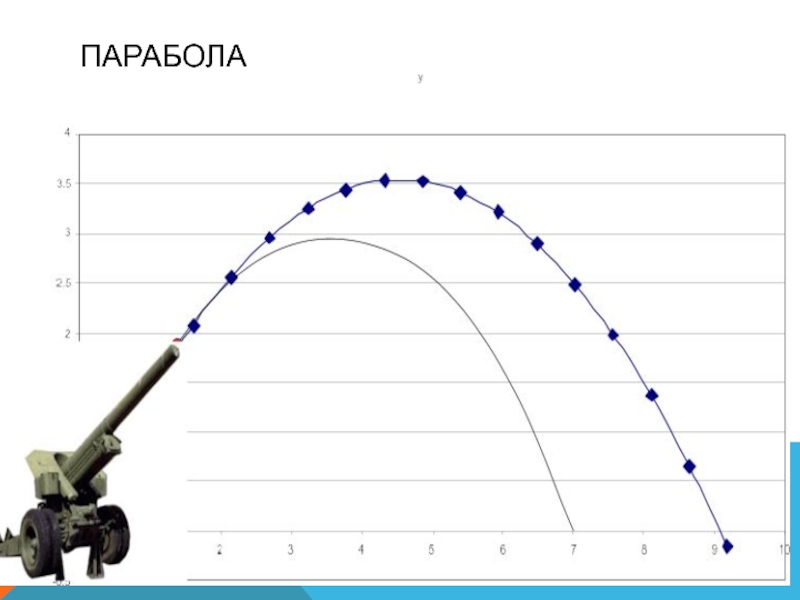
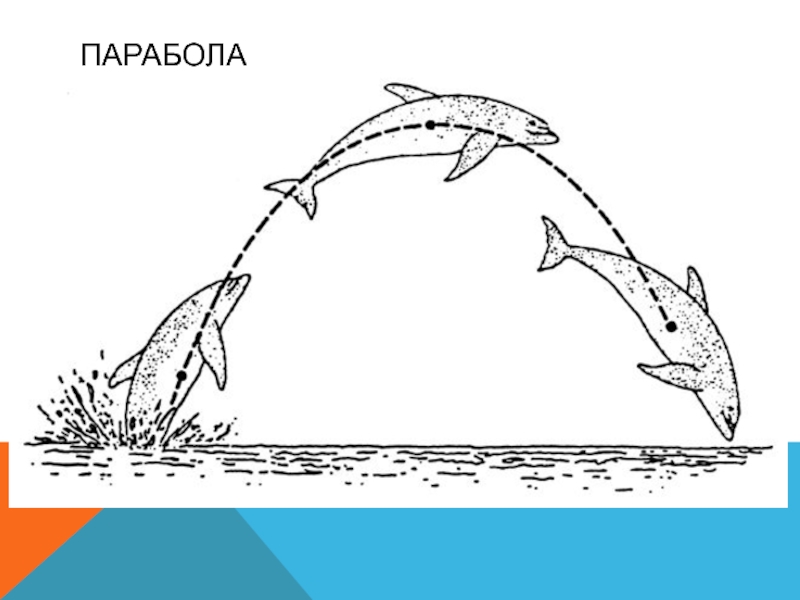
- ? АТ=6 смСлайд 17Эту замечательную кривую можно встретить в повседневной жизни. Например камень,
брошенный под углом к поверхности Земли, или стрела, пущенная из
лука также под углом к земле, двигаются по параболе. Траектории полёта тел изучались с древних времён в военных целях: было замечено, что снаряды летят по одинаковым кривым, а их вид меняется в зависимости от угла выстрела и начальной скорости.Парабола
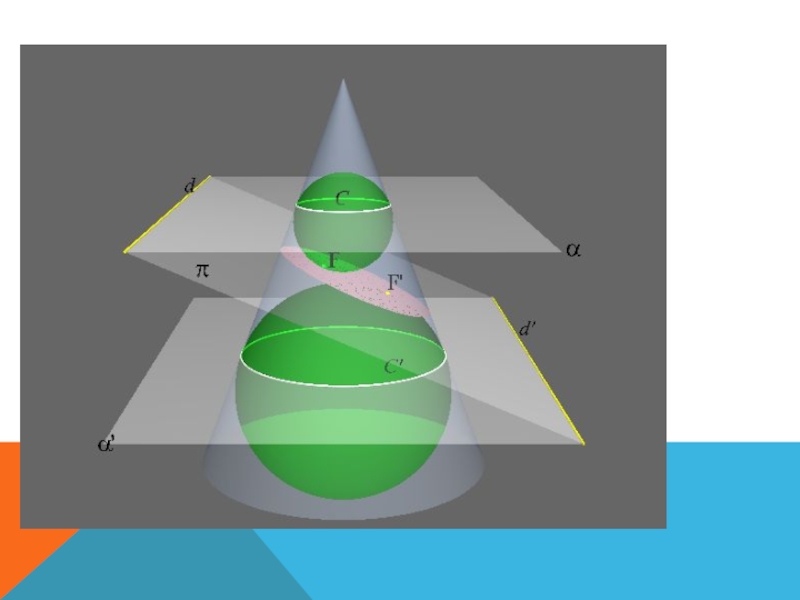
Слайд 241) Представьте, что конус разрезается плоскостью, параллельной основанию. Какая получится
фигура на плоскости разреза (в сечении)?
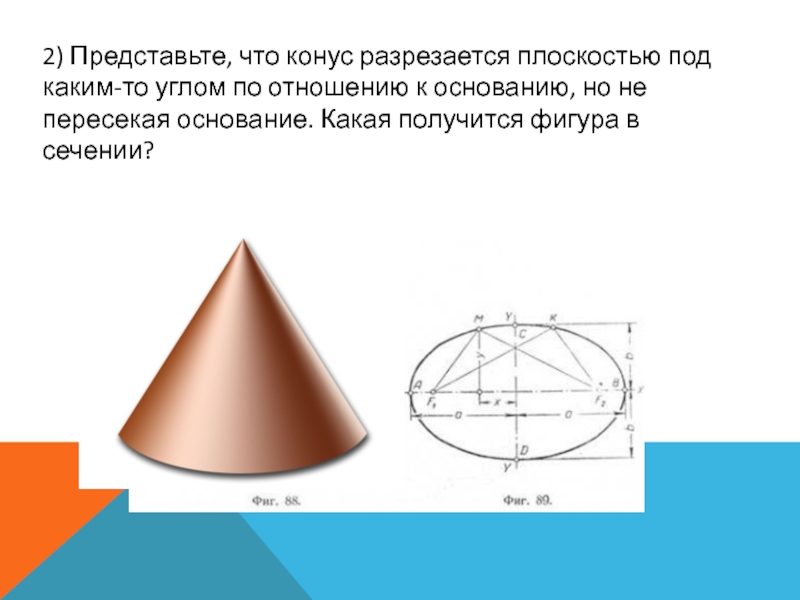
Слайд 252) Представьте, что конус разрезается плоскостью под каким-то углом по
отношению к основанию, но не пересекая основание. Какая получится фигура
в сечении?Слайд 26
3) Представьте, что конус разрезается плоскостью, проходящей через боковую поверхность
и основание. Какая получится фигура в сечении?
Слайд 30Спираль Архимеда
Слово «спираль» в переводе с латыни означает «изгиб». Такую
кривую первым рассмотрел Архимед в 225 году до н.э. в
своём сочинении «О спиралях», но узоры в виде спиралей были обнаружены в захоронениях бронзового века, их можно увидеть на греческих вазах и на кельтских украшениях.Нарисовать её на глиняном кувшине древнему художнику было не очень сложно: достаточно было вращать гончарный круг и одновременно смещать кисть в фиксированном направлении от центра к краю с постоянной скоростью.
Слайд 33Паук плетёт паутину по спирали.
Головка подсолнуха состоит из спиралей Архимеда,
одни из которых закручены по часовой стрелке, другие - против.
Слайд 37МЫ все живем в пределах синусоиды.
То на плаву, то утопая.
Границы
для падения и взлета.
Жизнь – синусоида. Не обессудь.
То, чем один
заканчивает путь,Другому служит точкою отсчета.
Слайд 43ЭТО КАРДИОИДА. ТАКОЕ НАЗВАНИЕ ОНА ПОЛУЧИЛА ИЗ-ЗА СХЕМАТИЧНОГО СХОДСТВА С
СЕРДЦЕМ (ПО ГРЕЧЕСКИ ΚΑΡΔΊΑ — СЕРДЦЕ, ΕἾΔΟΣ — ВИД). НАЗВАНИЕ
ПРИДУМАЛ ИТАЛЬЯНСКИЙ МАТЕМАТИК ДЖОВАННИ КАСТИЛЬОНИ (1708 – 1791).
Слайд 48- Прямолинейный желоб?
- Итальянский ученый Галилео Галилей (16-17 в.в.)
: желоб выгнуть по дуге окружности.
- Швейцарский ученый Иоганн Бернулли
(1696 г.) установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз (рис. 217, в)Слайд 53ГИПОЦИКЛОИДА?
Исследование:
Итоги исследования: ________________________________________________________________________________________________________________________________________________________________________________________________
Слайд 57Передо мной овал пруда, Я – с удочкой, рыбачу! Овал похож чуть-чуть
на круг,
А чем? Реши задачу!
В кардиоиде круг за кругом,
Друг за
другом
И около друга
Две души, две спирали бегут.
Там и тут, все бегут и бегут...Поэзия о кривых