Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приемы устного умножения
Содержание
- 1. Приемы устного умножения
- 2. Приемы устного умножения Руководитель: Полетавкина Людмила ДмитриевнаМОБУ СОШ с.В-Авзян2013 год
- 3. Сейчас, на этапе стремительного развития информатики и
- 4. Объектом исследования являются алгоритмы счета. Предметом
- 5. Задачи: - рассмотреть некоторые приемы устного
- 6. В Средние века совсем немногие владели
- 7. При работе я пользовалась следующими методами: поисковый
- 8. Актуальность данной темы заключается в том, что
- 9. Результаты анкетирования: Для того чтобы выяснить, знают
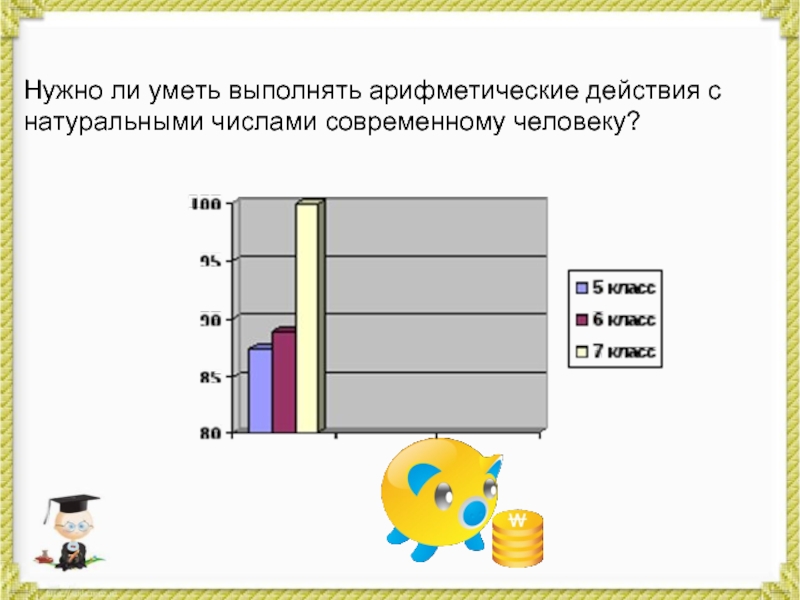
- 10. Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
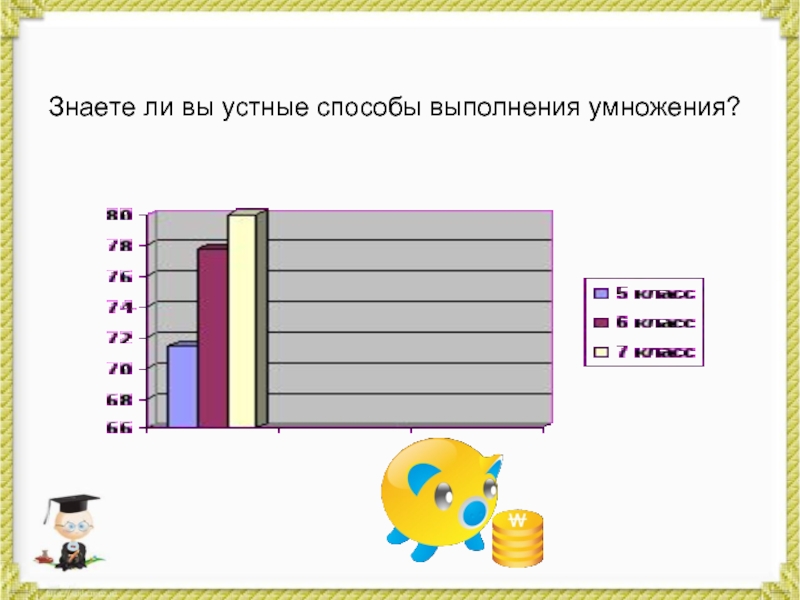
- 11. Знаете ли вы устные способы выполнения умножения?
- 12. Этот опрос показал, что современные школьники не
- 13. Умножение на 1132 · 11 = 3+2=532543
- 14. Умножение на 2524 · 25 = 24
- 15. Умножение на себя двухзначных чисел , оканчивающихся
- 16. А теперь сами попробуйте:45 · 45 =75 · 75 =85² =15² =Проверим202556257225225
- 17. Пальцевый счет при запоминании таблицы умножения.
- 18. Например, нужно умножить 6 на 7. Зажимаем
- 19. Еще один пример: необходимо умножить 8 на
- 20. А теперь сами попробуйте:7 · 6=5 · 8 =Проверим4240
- 21. Существует немало способов запоминания — в стихах, картинках, играх.
- 22. Допустим, нам надо умножить 3 на 9. Чтобы
- 23. А теперь сами попробуйте:7 · 9 =9 · 4 =5 · 9 =9 · 9 =Проверим63364581
- 24. А этому ,вас учили?
- 25. Мало кто знает, но японцы настоящие маньяки
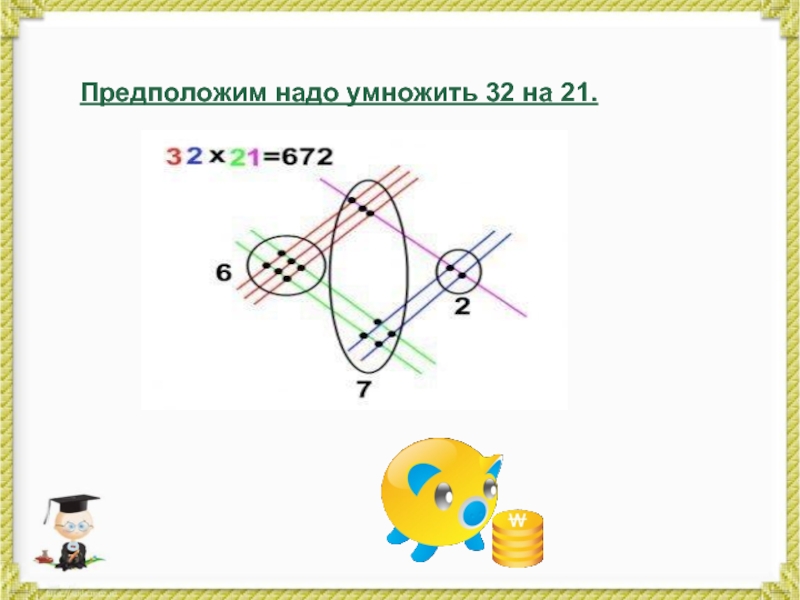
- 26. Предположим надо умножить 32 на 21.
- 27. На листе бумаги поочередно рисуем линии, количество
- 28. А теперь сами попробуйте:12 · 34 =17 · 54 =Проверим408918
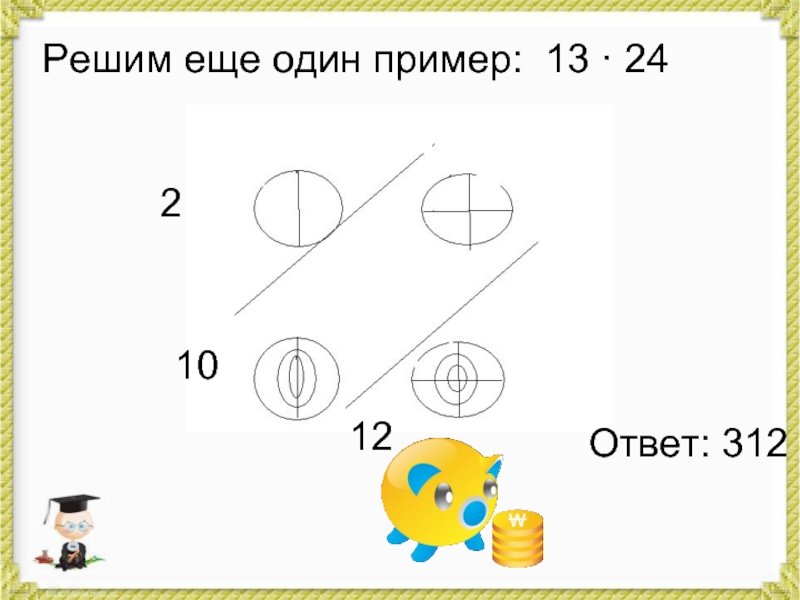
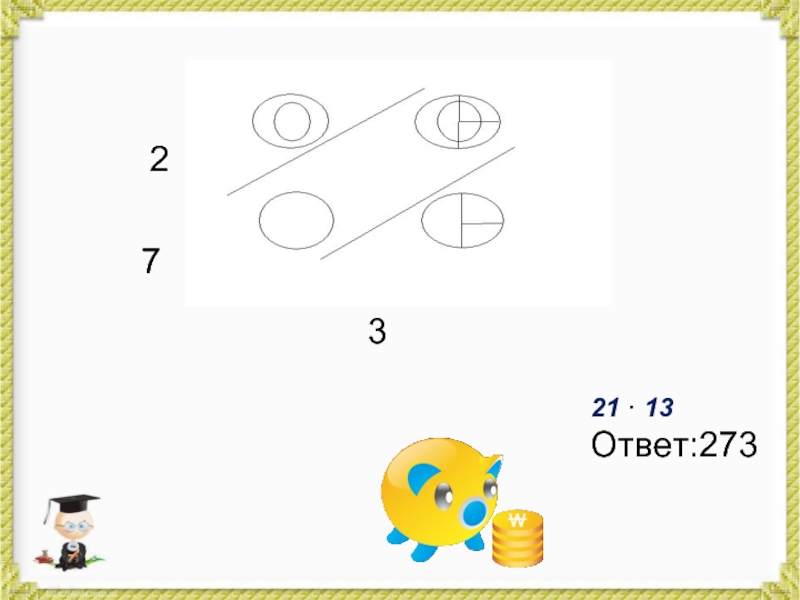
- 29. Решим еще один пример: 13 · 2421012Ответ: 312
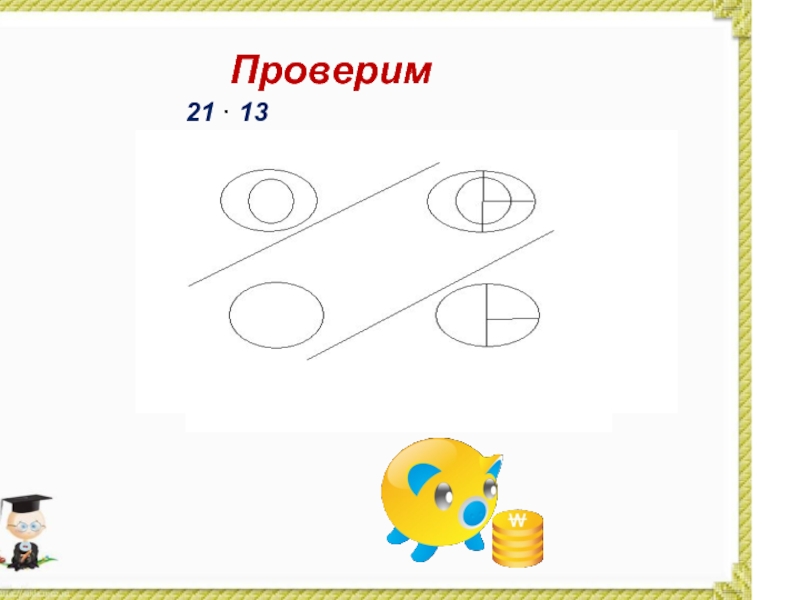
- 30. А теперь сами попробуйте: 21 · 13
- 31. Проверим21 · 13
- 32. 27321 · 13 Ответ:273
- 33. А теперь сами попробуйте:34 · 12 =23 · 14 =Проверим408322
- 34. 7 · 9 =9 · 4 =5
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Учебно-исследовательская работа
Автор: Полетавкина Дарья Сергеевна, 8б класс, средняя общеобразовательная
школа,с.В-Авзян.
Слайд 2Приемы устного умножения
Руководитель: Полетавкина Людмила Дмитриевна
МОБУ СОШ с.В-Авзян
2013 год
Слайд 3
Сейчас, на этапе стремительного развития информатики и вычислительной техники, современные
школьники не хотят утруждать себя счетом в уме. Поэтому мы
сочли важным показать не только то, что сам процесс выполнения действия может быть интересным, но и что, хорошо усвоив приёмы быстрого счета, можно поспорить и с ЭВМ.Слайд 4Объектом исследования являются алгоритмы счета. Предметом исследования выступает процесс вычисления. Цель: изучить
нестандартные приемы вычислений.
Слайд 5Задачи: - рассмотреть некоторые приемы устного умножения и на конкретных примерах
показать преимущества их использования,
-показать эти приемы другим учащимся,
-применять эти знания
на практике.Слайд 6 В Средние века совсем немногие владели искусством умножения. Редкий
аристократ мог похвастаться знанием таблицы умножения, даже если он окончил
европейский университет.Гипотеза:
Гипотеза:
В старину говорили: « Умножение – мое мученье». Значит, раньше было сложно и трудно умножать. Прост ли наш современный способ умножения?
За тысячелетия развития математики было придумано множество способов умножения чисел.
Слайд 7При работе я пользовалась следующими методами:
поисковый метод с использованием научной
и учебной литературы, а также поиск необходимой информации в сети
Интернет;практический метод выполнения вычислений с применением нестандартных алгоритмов счета;
анализ полученных в ходе исследования данных.
Слайд 8Актуальность данной темы заключается в том, что использование нестандартных приемов
в формировании вычислительных навыков усиливает интерес учащихся к математике и
содействует развитию математических способностей. Захотелось узнать способы умножения, сравнить их с нашим сегодняшним действием умножения.
Слайд 9Результаты анкетирования:
Для того чтобы выяснить, знают ли современные школьники
другие способы выполнения арифметических действий, кроме умножения столбиком и деления
«уголком» и хотели бы узнать новые способы, был проведен устный опрос. Было опрошено 20 учащиеся 5-7 классов.Слайд 10
Нужно ли уметь выполнять арифметические действия с натуральными числами современному
человеку?
Слайд 12
Этот опрос показал, что современные школьники не знают других способов
выполнения действий, так как редко обращаются к материалу, находящемуся за
пределами школьной программы.ВЫВОД:
Слайд 13Умножение на 11
32 · 11 =
3+2=5
3
2
5
43 · 11 =
4 3
4+3=7
7
57 · 11 = 6 7
2
5+7=12
А теперь
сами попробуйте:25 · 11 =
54 · 11 =
49 · 11 =
68 · 11 =
Проверим
275
594
539
748
запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр. Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа.
Слайд 14Умножение на 25
24 · 25 = 24 · 100 :
4 = 2400 : 4 = 600
36 · 25 =
3600 : 4 = 900А можно наоборот:
24·25=24 : 4 · 100 = 600
36·25=36 : 4 · 100 = 900
А теперь сами попробуйте:
16 · 25 =
44 · 25 =
48 · 25 =
68 · 25 =
Проверим
400
1100
1200
1700
Чтобы умножить число на 25, нужно его умножить на 100/4, то есть умножить на 100 и разделить на 4.
Слайд 15Умножение на себя
двухзначных чисел , оканчивающихся на 5
25 ·
25 = 625
2·3=6
35 · 35 = 1225
3·4=12
Правило:
Число десятков умножаем на
следующую за ним в ряду натуральных чисел цифру, а на конце у этих произведений всегда стоит 25
65² = 65 · 65 = 4225
6 ·7 = 42
Слайд 17
Пальцевый счет при запоминании таблицы умножения.
Прием пальцевого счета
при получении значений табличного умножения является одним из древнейших вычислительных
приемов. Следует заметить, что многие учителя не признают правомочности приемов пальцевого счета при изучении табличного сложения и табличного умножения, придерживаясь мнения, что их результаты необходимо учить наизусть. Выучить всю таблицу наизусть могут не все дети. Учителя математики знают, что и среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения. Для детей младшего школьного возраста с преобладающим кинестезическим восприятием и кинестезической памятью прием пальцевого счета при освоении таблицы умножения может быть рекомендован как вспомогательный. Для того чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы умножения числа 4.Слайд 18Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих
руках в кулак, а затем на каждой руке отгибаем столько
пальцев, насколько каждый множитель больше, чем пять. На двух руках отогнуто три пальца - это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой - четыре пальца эти числа перемножаем 3 * 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.
Слайд 19Еще один пример: необходимо умножить 8 на 9. Отгибаем
на одной руке три пальца, а на другой руке -
четыре пальца (на столько каждый множитель больше, чем пять). Отогнуто 7 пальцев - это десятки в искомом числе. Перемножаем число загнутых пальцев обеих рук: 2 * 1 = 2. Прибавляем это количество к числу десятков 70 + 2 = 72.Таким образом, 9 * 8 = 72.
Слайд 21Существует немало способов запоминания — в стихах, картинках, играх. Мы предлагаем вам еще
один интересный способ — таблицу умножения на пальцах. Этот метод подходит для
заучивания правил умножения на девятку. Зачастую примеры с умножением на 9 даются детям труднее всего.Итак, всё, что вам понадобится — это десять пальцев рук. Положите ладони на стол. Мысленно дайте каждому пальцу, начиная от мизинца левой руки и заканчивая мизинцем правой, свой номер от 1 до 10.
Вот так:
Слайд 22Допустим, нам надо умножить 3 на 9. Чтобы вычислить ответ, надо
найти палец под номером 3 и поднять его. А затем посмотреть, сколько пальцев
осталось лежать справа и слева. Количество пальцев слева от поднятого пальца (в нашем случае их 2) — это десятки, количество пальцев справа (у нас это 7) — это единицы. Итого, получаем — 2 и 7, то есть 27.Слайд 25Мало кто знает, но японцы настоящие маньяки в умножении чисел
.
В этом плане они больше походят на пришельцев с другой
планеты, чем на людей. Умножение "столбиком" слишком скучное и унылое занятие для их необычного типа мышления. Впитав с молоком матери иероглифическое письмо, японцы изощряются в умножении визуальными способами. Поскольку иероглиф у них обозначает сразу какое-то слово или даже фразу, то почему бы не изображать схожим образом число-ответ при умножении? Слайд 27На листе бумаги поочередно рисуем линии, количество которых определяется из
данного примера.
Сначала 32: 3 красные линии и чуть ниже -
2 синие. Затем 21: перпендикулярно уже нарисованным, рисуем сначала 2 зеленые, затем - 1 малиновую. ВАЖНО: линии первого числа рисуются в направлении из верхнего левого угла в нижний правый, второго числа - из нижнего левого, в верхний правый. Затем считаем количество точек пересечения в каждой из трех областей (на рисунке области обозначены в виде окружностей). Итак, в первой области ( область сотен) - 6 точек, во второй (область десятков) - 7 точек, в третьей (область единиц) - 2 точки. Следовательно ответ: 672.Слайд 347 · 9 =
9 · 4 =
5 · 9 =
9
· 9 =
Проверим
63
36
45
81
При знакомстве с научной литературой обнаружили более
быстрые и надежные способы умножения. Поэтому изучение действия умножения – тема перспективная.
Возможно, что с первого раза у многих не получится быстро, с ходу выполнять эти или другие подсчеты. Пусть сначала не получится использовать прием, показанный в работе.Рассмотренные мною способы умножения не такие сложные и могут повседневно использоваться учащимися. Они познавательны и интересны.
Я знаю, что существуют еще много интересных способов вычислений. И я соберу целую коллекцию таких примеров рационального вычисления.
Заключение.