Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Призма 9 класс
Содержание
- 1. Призма 9 класс
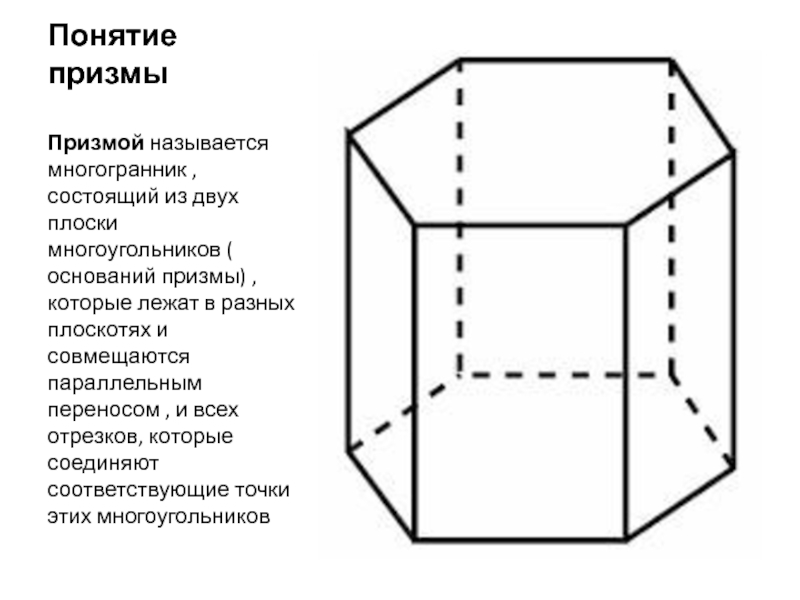
- 2. Понятие призмыПризмой называется многогранник , состоящий из
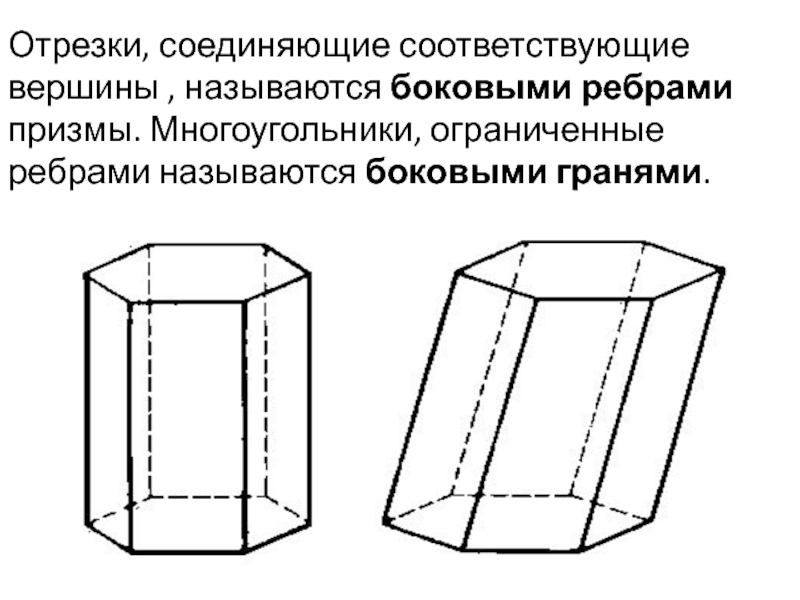
- 3. Отрезки, соединяющие соответствующие вершины , называются боковыми ребрами призмы. Многоугольники, ограниченные ребрами называются боковыми гранями.
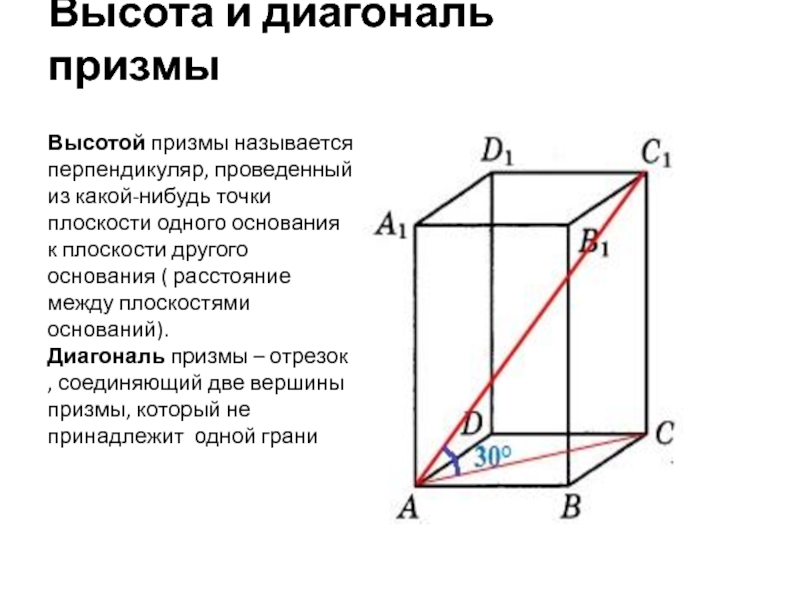
- 4. Высота и диагональ призмыВысотой призмы называется перпендикуляр,
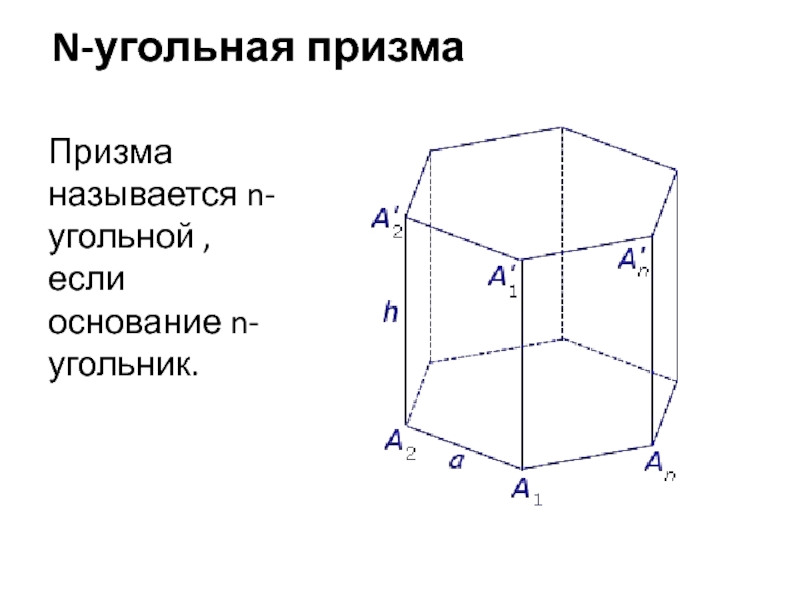
- 5. N-угольная призмаПризма называется n-угольной , если основание n-угольник.
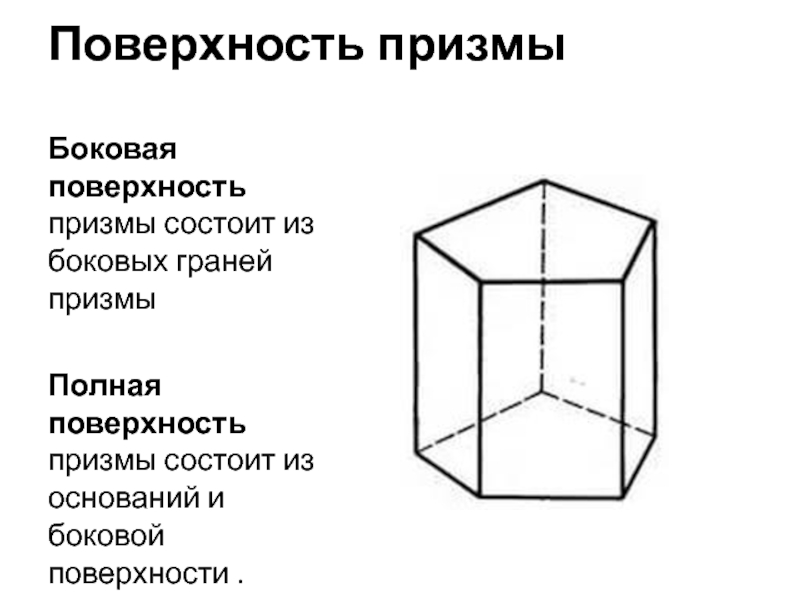
- 6. Поверхность призмыБоковая поверхность призмы состоит из боковых
- 7. Свойства призмыОснования призмы – равные многоугольники, лежащие
- 8. Прямая призмаПрямая призма – это призма, все боковые ребра которой перпендикулярны основаниям.
- 9. Свойства прямой призмыОснования прямой призмы – равные
- 10. ПараллелепипедПараллелепипед, у которого боковые ребра перпендикулярны основанию,
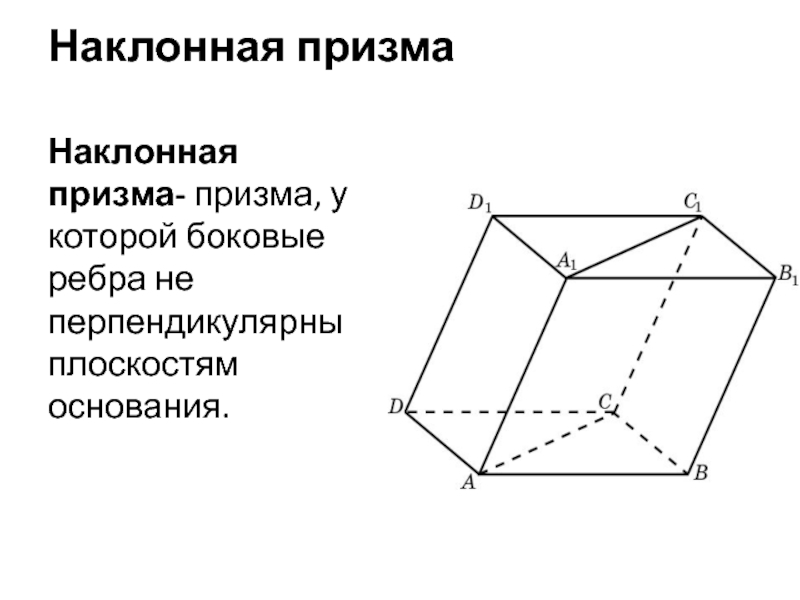
- 11. Наклонная призмаНаклонная призма- призма, у которой боковые ребра не перпендикулярны плоскостям основания.
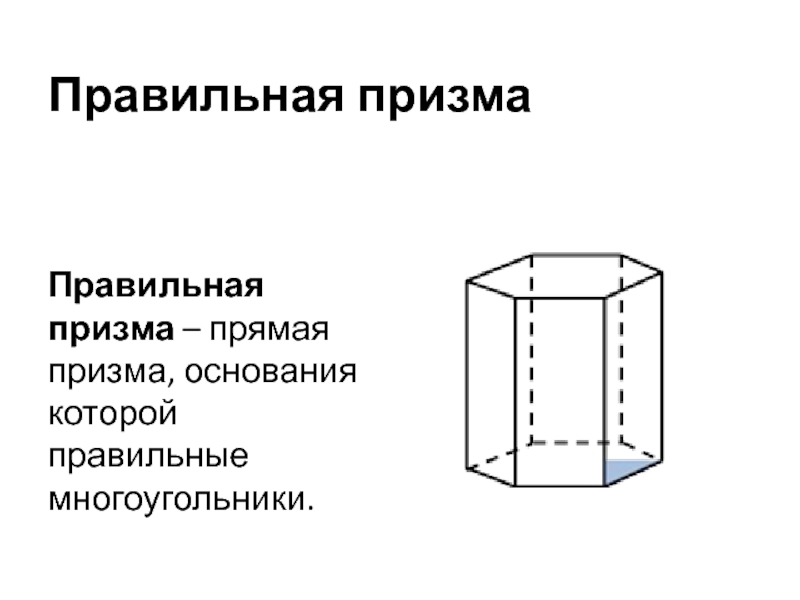
- 12. Правильная призмаПравильная призма – прямая призма, основания которой правильные многоугольники.
- 13. Свойства правильной призмыВсе свойства прямой призмы справедливы
- 14. Площадь поверхности и объем прямой призмыБоковая поверхность
- 15. Площадь поверхности и объем наклонной призмыБоковая поверхность
- 16. Призмы вокруг нас
- 17. Скачать презентанцию
Понятие призмыПризмой называется многогранник , состоящий из двух плоски многоугольников ( оснований призмы) , которые лежат в разных плоскотях и совмещаются параллельным переносом , и всех отрезков, которые соединяют соответствующие точки
Слайды и текст этой презентации
Слайд 3Отрезки, соединяющие соответствующие вершины , называются боковыми ребрами призмы. Многоугольники,
ограниченные ребрами называются боковыми гранями.
Слайд 4Высота и диагональ призмы
Высотой призмы называется перпендикуляр, проведенный из какой-нибудь
точки плоскости одного основания к плоскости другого основания ( расстояние
между плоскостями оснований). Диагональ призмы – отрезок , соединяющий две вершины призмы, который не принадлежит одной граниСлайд 6Поверхность призмы
Боковая поверхность призмы состоит из боковых граней призмы
Полная поверхность
призмы состоит из оснований и боковой поверхности .
Слайд 7Свойства призмы
Основания призмы – равные многоугольники, лежащие в параллельных плоскостях.
2.Боковые
ребра призмы параллельны и равны.
3.Боковые грани призмы –параллелограммы
Слайд 8Прямая призма
Прямая призма – это призма, все боковые ребра которой
перпендикулярны основаниям.
Слайд 9Свойства прямой призмы
Основания прямой призмы – равные многоугольники, которые лежат
в параллельных плоскостях.
Боковые ребра прямой призмы параллельны , равны и
перпендикулярны плоскостям оснований, т..е являются высотами призмы . Высота прямой призмы равна длине бокового ребра.Боковые грани прямой призмы – прямоугольники. Плоскости боковых граней перпендикулярны плоскостям оснований.
Слайд 10Параллелепипед
Параллелепипед, у которого боковые ребра перпендикулярны основанию, называется прямым.
Прямой параллелепипед
, основаниями которого является прямоугольники , называется прямоугольным.
Прямоугольный параллелепипед, у
которого все ребра равны, называется кубом.Слайд 11Наклонная призма
Наклонная призма- призма, у которой боковые ребра не перпендикулярны
плоскостям основания.
Слайд 12Правильная призма
Правильная призма – прямая призма, основания которой правильные многоугольники.
Слайд 13Свойства правильной призмы
Все свойства прямой призмы справедливы и для правильной
призмы. Кроме того :
Боковые грани правильной призмы – равные прямоугольники.
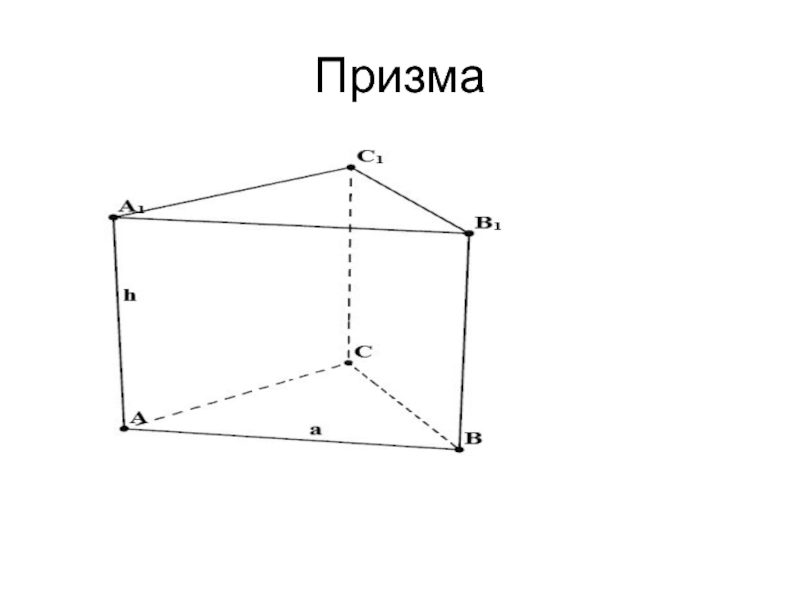
Площадь
боковой поверхности правильной n-угольной призмы со стороной основания а и высотой h вычисляется по формуле : Sбок=n*a*hСлайд 14Площадь поверхности и объем прямой призмы
Боковая поверхность : Sбок=Росн*Н,
где Росн
– периметр основания, Н-высота.
Полная поверхность:
Sполн=Sбок+2Sосн
Объем:
V= Sосн*H
Где Sосн – площадь
основания призмы, Н- высота.Слайд 15Площадь поверхности и объем наклонной призмы
Боковая поверхность : Sбок=Pпер*l, где
Рпер- периметр перпендикулярного сечения, l – длина бокового ребра
Полная поверхность
: Sполн=Sбок+2SоснОбъем : V=Sпер*l или V=S осн *H , где Sпер-площадь перпендикулярного сечения, l – боковое ребро.