Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Призма: виды и особенности
Содержание
- 1. Призма: виды и особенности
- 2. План лекцииПонятие и чертёжЭлементы призмыОбщие свойства призмВиды призм и их особенностиПоверхность призмСечения призмПризмы вокруг нас
- 3. Понятие призмыПризма - это многогранник
- 4. Элементы призмы
- 5. Элементы призмыОснования – это грани, совмещаемые параллельным
- 6. Общие свойства призмыОснования призмы равныОснования призмы лежат
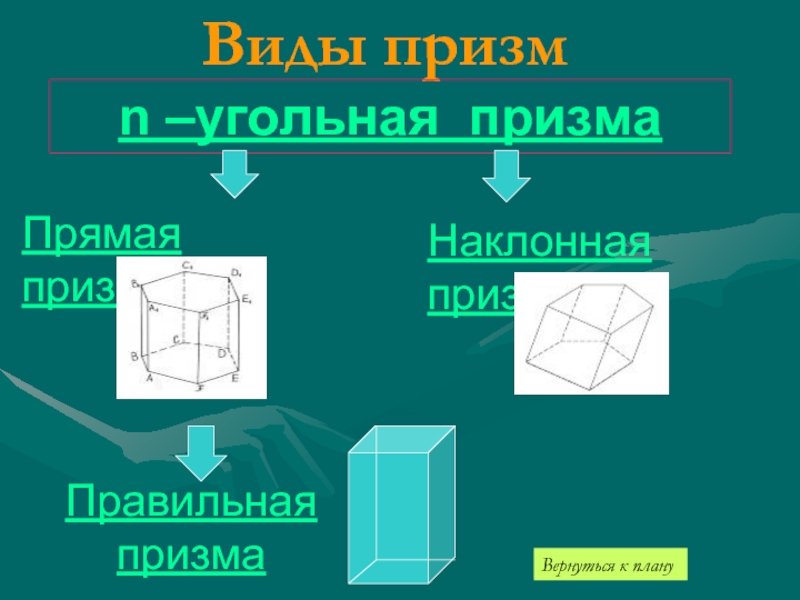
- 7. Виды призмn –угольная призма Прямая призмаНаклонная призмаПравильная призмаВернуться к плану
- 8. N-угольная призма- это призма, в основании которой лежит n -угольникТреугольная призмаЧетырёхугольная призмаШестиугольная призма
- 9. Прямая призма- это призма, боковые рёбра которой перпендикулярны основаниюЕё высота равна боковому ребруb
- 10. Правильная призма- это прямая призма, основанием которой
- 11. Наклонная призма- это призма, боковые рёбра которой не перпендикулярны основанию.
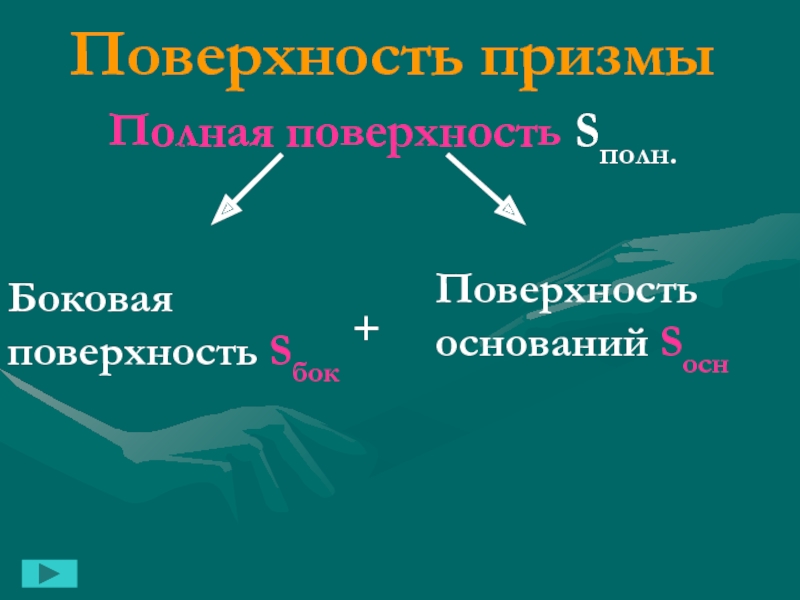
- 12. Поверхность призмыПолная поверхность Sполн.Поверхность – это сумма площадей граней+
- 13. Боковая поверхность прямой призмыТеорема: Боковая поверхность
- 14. Доказательство теоремыБоковые грани прямой призмы – прямоугольники
- 15. Особые сечения призмыДиагональное сечение – это сечение
- 16. Призмы вокруг нас
- 17. Скачать презентанцию
План лекцииПонятие и чертёжЭлементы призмыОбщие свойства призмВиды призм и их особенностиПоверхность призмСечения призмПризмы вокруг нас
Слайды и текст этой презентации
Слайд 1призма
Слайд – лекция
Составлена учителем математики Поназыревской средней общеобразовательной школы Орловой
Н. В.
Слайд 2План лекции
Понятие и чертёж
Элементы призмы
Общие свойства призм
Виды призм и их
особенности
Поверхность призм
Сечения призм
Призмы вокруг нас
Слайд 3Понятие призмы
Призма -
это многогранник состоящий из двух
плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом,
и всех отрезков, соединяющих соответствующие точки этих многоугольников.
Чертёж призмы
Вернуться к плану
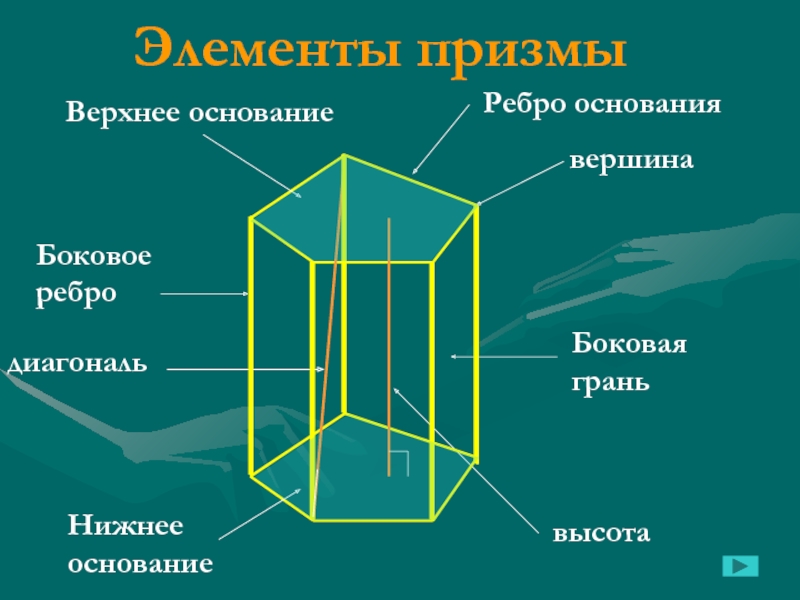
Слайд 5Элементы призмы
Основания –
это грани, совмещаемые параллельным переносом.
Боковая грань –
это грань, не являющаяся основанием.
Боковые рёбра –
это отрезки, соединяющие
соответствующие вершины оснований.Вершины –
это точки, являющиеся вершинами оснований.
Высота –
это перпендикуляр, опущенный из одного основания на другое.
Диагональ –
это отрезок, соединяющий две вершины, не лежащие в одной грани.
Вернуться к плану
Слайд 6Общие свойства призмы
Основания призмы равны
Основания призмы лежат в параллельных плоскостях
У
призмы боковые рёбра параллельны и равны
Любая боковая грань является параллелограммом
Вернуться
к плануСлайд 8N-угольная призма
- это призма, в основании которой лежит n -угольник
Треугольная
призма
Четырёхугольная призма
Шестиугольная призма
Слайд 9Прямая призма
- это призма, боковые рёбра которой перпендикулярны основанию
Её высота
равна
боковому ребру
b
Слайд 10Правильная призма
- это прямая призма, основанием которой является правильный многоугольник.
В
основании равносторонний треугольник
В основании квадрат
В основании правильный
6-угольник
Слайд 13Боковая поверхность прямой призмы
Теорема:
Боковая поверхность прямой призмы равна
произведению периметра основания на длину бокового ребра.
Дано: прямая n-угольная призма,
a1 , а2 … аn -стороны основания, l - боковое ребро.Доказать: Sбок=Pосн l
Вернуться к плану
Слайд 14Доказательство теоремы
Боковые грани прямой призмы – прямоугольники у которых сторонами
являются стороны основания призмы и боковые рёбра призмы
S1=a1l , S2=a2l …Sn= an lSбок= S1+S2+…Sn=a1l +a2l +an l =
(a1 +a2 +…an) l =Pосн l
Теорема доказана
Слайд 15Особые сечения призмы
Диагональное сечение – это сечение проходящее через два
боковых ребра, не принадлежащих одной грани.
Перпендикулярное сечение – это сечение,
проходящее перпендикулярно боковым ребрам.Вернуться к плану
Теги