Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки делимости
Содержание
- 1. Признаки делимости
- 2. В арифметике много разделов и один из
- 3. Старинная восточная притча: Давным-давно жил-был старик, который,
- 4. При́знак дели́мости — алгоритм, позволяющий сравнительно быстро
- 5. ПРИМЕНЕНИЕ:Как правило, признаки делимости применяются при ручном и устном счёте
- 6. Два целых числа a и b называются
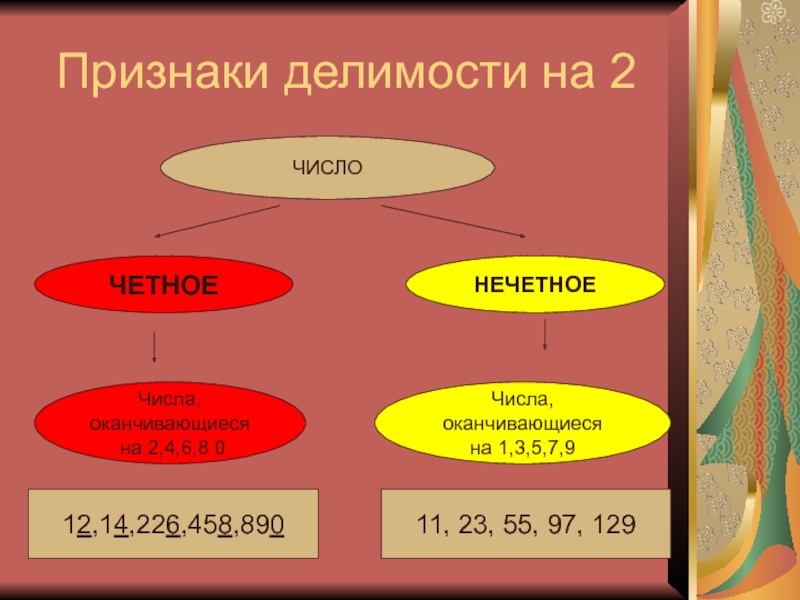
- 7. Признаки делимости на 2ЧИСЛО ЧЕТНОЕНЕЧЕТНОЕЧисла, оканчивающиеся на 2,4,6,8 0Числа, оканчивающиеся на 1,3,5,7,912,14,226,458,89011, 23, 55, 97, 129
- 8. ПРАВИЛО:Натуральные числа, запись которых оканчивается четной цифрой делятся на 2
- 9. ПРИМЕР:Делится ли число 88 на 2 без
- 10. Примером применения четных и нечетных чисел в
- 11. ПРАВИЛО:Если сумма цифр натурального числа делится на 3,то и все число делиться на 3
- 12. Давайте разберем простой пример! Делится ли число
- 13. Проверим делимость на 3 числа
- 14. ПРАВИЛО:Если сумма цифр натурального числа делится на 9, то и все числоДелится на 9 без остатка
- 15. Пример:129 делится на 9?Нет. Так как, сумма
- 16. ПРАВИЛО: Натуральные числа,запись которых оканчивается на 0 и 5 делиться на 5 без остатка
- 17. Пример: 10, 25, 625, 990 делятся на
- 18. ПРАВИЛОНатуральные числа,запись которых оканчивается на 0,делятся на 10 без остатка
- 19. ПримерЧисла 50, 100, 2600, 9000 делятся на
- 20. Существует При́знак Паска́ля — метод, позволяющий получить
- 21. Задача 1Условие: Покупатель взял в магазине пакет
- 22. ОТВЕТ:. Число 225 не делится на 2 без остатка, следовательно, кассирша ошиблась.
- 23. Задача 2 Делимое в шесть раз
- 24. Признаки делимости на 4, 6, 7, 8,
- 25. Успехов в учебе!
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Старинная восточная притча: Давным-давно жил-был старик, который, умирая, оставил своим трем
сыновьям 19 верблюдов. Он завещал старшему сыну половину, среднему –
четвертую часть, а младшему – пятую. Не сумев найти решения самостоятельно (ведь задача в «целых верблюдах» решения не имеет), братья обратились к мудрецу. - О, мудрец!- сказал старший брат. - Отец оставил нам 19 верблюдов и велел разделить между собой: старшему – половину, среднему – четверть, младшему – пятую часть. Но 19 не делится ни на 2, ни на 4, ни на 5. Можешь ли ты, о, достопочтенный, помочь нашему горю, ибо мы хотим выполнить волю отца? - Нет ничего проще, - ответил им мудрец. – Возьмите моего верблюда и идите домой. Братья дома легко разделили 20 верблюдов пополам, на 4 и на 5.Старший брат получил 10, средний – 5, а младший – 4 верблюда. При этом один верблюд остался (10+5+4=19). Раздосадованные, братья вернулись к мудрецу и пожаловались: - О, мудрец, опять мы не выполнили волю отца! Вот этот верблюд – лишний. - Это не лишний, - сказал мудрец,- это мой верблюд. Верните его и идите домой.Слайд 4При́знак дели́мости — алгоритм, позволяющий сравнительно быстро определить, является ли
число кратным заранее заданному. Если признак делимости позволяет выяснить не
только делимость числа на заранее заданное, но и остаток от деления, то его называют признаком равноостаточностиСлайд 6Два целых числа a и b называются равноделимыми на m,
если либо они оба делятся на m, либо оба не
делятся Например: 15 и 30 делятся на 3 без остатка 16 и 31 не делятся на 3 без остатка Два целых числа a и b называются равноостаточными, когда при делении на натуральное число m они дают одинаковые остатки 1/8=0,125 и 17/8=2,125Слайд 7Признаки делимости на 2
ЧИСЛО
ЧЕТНОЕ
НЕЧЕТНОЕ
Числа, оканчивающиеся
на 2,4,6,8 0
Числа, оканчивающиеся
на 1,3,5,7,9
12,14,226,458,890
11, 23, 55, 97, 129
Слайд 9ПРИМЕР:
Делится ли число 88 на 2 без остатка?
Да, так как
число 88 оканчивается на четную цифру.
ПОПРОБУЙ САМ!
Делится ли число 96
на 2 без остатка?
ОТВЕТ: Да!
так как число 96
оканчивается
на четную цифру.
Слайд 10Примером применения четных и нечетных чисел в повседневной жизни могут
служить расписания движения поездов, когда поезда отправляются только по четным
или только по нечетным числам.Слайд 12Давайте разберем простой пример! Делится ли число 159 на 3?
Сложим
все числа 1 + 5 + 9 = 15
15 делится
на 3 : 15 /3 = 5и дает в результате 5.Если разделить на 3. Взятое нами число
159 : 3 = 53
Таком образом этот признак можно использовать для любого числа
ПОПРОБУЙ САМ!
Делится ли число 196 на 3 без остатка?
Ответ: нет!
1+9+6=16
16:3 = 5 (ост. 3)
Слайд 13Проверим делимость на 3 числа
29 443 680 100 259
(двадцать девять триллионов четыреста сорок
три миллиарда шестьсот восемьдесят миллионов сто тысяч двести пятьдесят девять). 1. Находим сумму цифр:2 + 9 + 4 + 4 + 3 + 6 + 8 + 0 + 1 + 0 + 0 + 2 + 5 + 9 = = 53
Теперь находим сумму цифр числа 53 : 5 + 3 = 8
Число 8 не делится на число 3, следовательно число 29 443 680 100 259 не может быть поделено на число 3 без остатка:
29 443 680 100 259 : 3 = 9 814 560 033 419 и 2 в остатке
Слайд 14ПРАВИЛО:
Если сумма цифр
натурального числа
делится на 9, то и
все число
Делится на 9 без остатка
Слайд 15Пример:
129 делится на 9?
Нет. Так как, сумма цифр числа 129
(12) не делится на 9 без остатка.
делится на 9?
Да.
Так как, сумма цифр числа 144 (9) делится на 9 без остатка. ПОПРОБУЙ САМ!
Делится ли число 962 на 9?
ОТВЕТ: нет!
Так как сумма цифр числа 962
На 9 не делится без остатка
Слайд 17Пример:
10, 25, 625, 990 делятся на 5 без остатка,
как эти числа оканчиваются на 0 и 5
11, 63, 82
не делятся на 5 без остатка, так как оканчиваются не на 0 и 5ПОПРОБУЙ САМ!
Делится ли 495 на 5 без остатка?
Ответ: ДА!
Так как число 495 оканчивается на 5,то
Оно делится на 5 без остатка
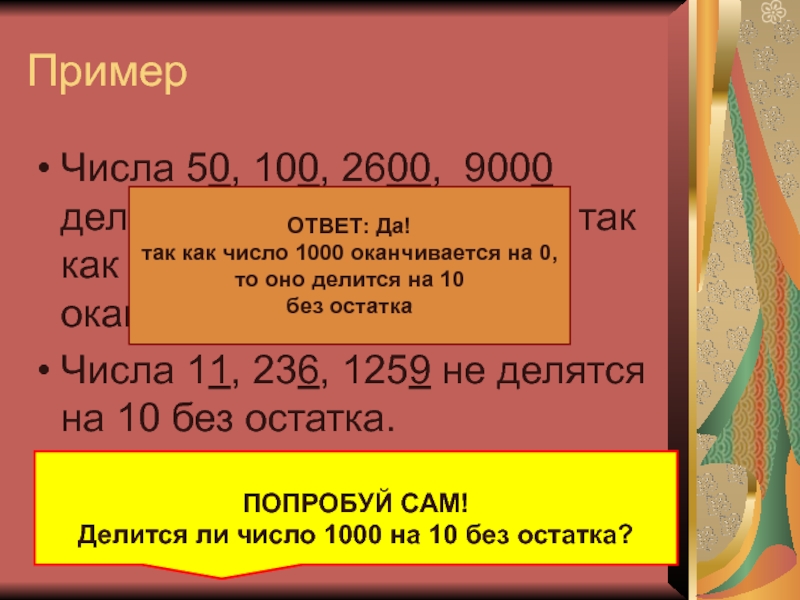
Слайд 19Пример
Числа 50, 100, 2600, 9000 делятся на 10 без остатка,
так как запись этих чисел оканчивается на 0
Числа 11, 236,
1259 не делятся на 10 без остатка.
ПОПРОБУЙ САМ!
Делится ли число 1000 на 10 без остатка?
ОТВЕТ: Да!
так как число 1000 оканчивается на 0,
то оно делится на 10
без остатка
Слайд 20Существует При́знак Паска́ля — метод, позволяющий получить признаки делимости на
любое число. Своего рода «универсальный признак делимости».
Например:
остаток от
деления числа на 2 равен остатку от деления его последней цифры на 2, или обычно: число делится на 2, если его последняя цифра чётна.Мы разобрали наиболее часто используемые признаки делимости: на 2, 3, 5, 9, 10.
Слайд 21Задача 1
Условие: Покупатель взял в магазине пакет молока, стоимостью 126
тенге,
коробку творога, стоимостью 96 тенге
Когда кассирша выбила чек на
225 тенге, покупатель потребовал проверить расчет и исправить ошибку.Как определил покупатель, что счет неверен ?
Слайд 23 Задача 2 Делимое в шесть раз больше делителя, а делитель в
шесть раз больше частного.
Чему равны делимое, делитель и частное?
Искомое частное равно 6; оно показывает, во сколько раз делимое больше делителя. Делитель в 6 раз больше частного и равен 36.
Делимое в 6 раз больше делителя и равно 216.
Слайд 24Признаки делимости на 4, 6, 7, 8, 11
На 4
делятся если
На 6 делятся если
На 7 делятся
если На 8 делятся если
На 11 делятся если