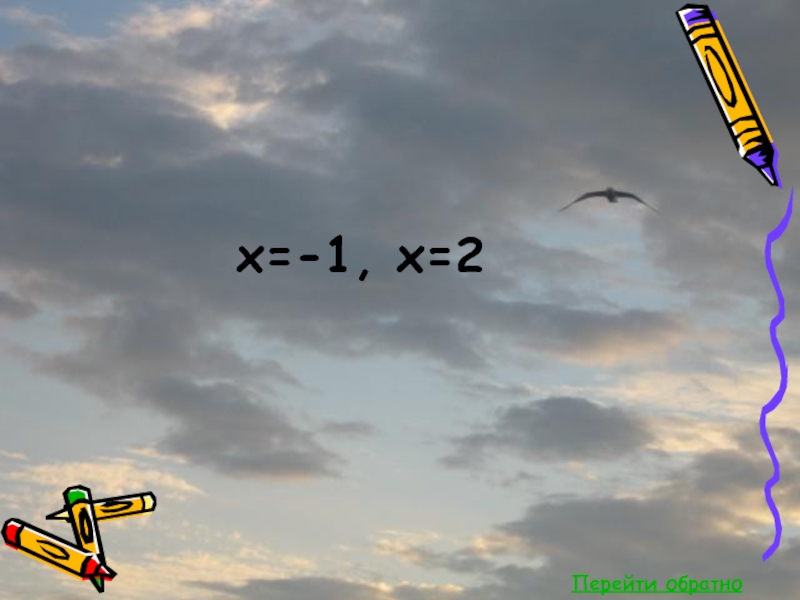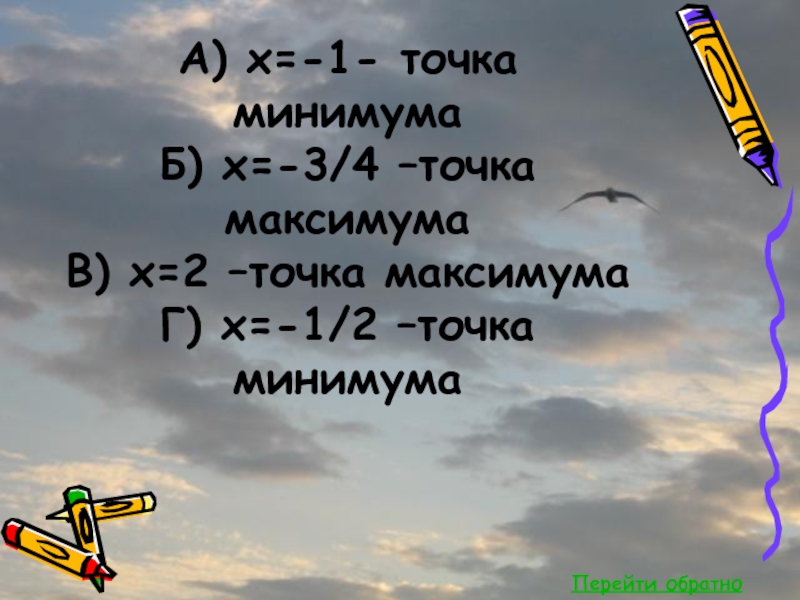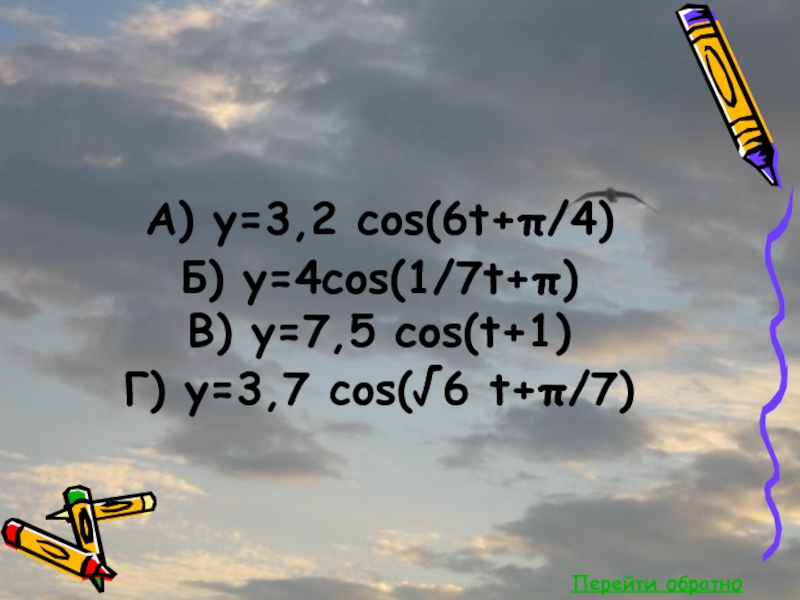Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная и её применение
Содержание
- 1. Производная и её применение
- 2. Под темы:ПроизводнаяПрименение производной к приближенным вычислениям в геометрии и физикеПрименения производной к исследованию функций
- 3. Найдите десятичные приближение чисел по недостатку и
- 4. Найдите предел, к которому х→ 3 стремится
- 5. Найдите производные функции:Примеры:А) g(x)=2х-3Б) g(x)=х2-2В) g(x)=х2-3х+4Г) g(x)=3х2-6хОтветы
- 6. Найдите производную функции:А) f(x)=(sin π /2-2x)3;Б) f(x)=(2x cos 0+x2)2;В) f(x)=(2x sin π/6+1)2;Г) f(x)=(2x2tg π/4-sin π)3Ответы
- 7. Найдите производные функции:А) y=cos(5-3x)Б) y=sin(3-2x)В) y=ctg(2-5x)Ответы
- 8. Найдите производные функции:А) g(x)=2x3-3sin 3xБ) g(x)= √(x-2) +cos(x2-2)Ответы
- 9. Найдите производные функции:А) h(x)=tgx+tg3x/1-tgx*tg3xБ) h(x)=cos24x+sin24xВ)h(x)=1-cos2x/sinxОтветы
- 10. Найдите значение производной функции y=cos x при:А) x=π/2Б) x=-π В)x=π/6Ответы
- 11. Сравните значения выражений:А) f’(0) и g’(π/2)Б) f’(π/4) и g’(π/3)еслиf(x)=tgx и g(x)=ctgx Ответы
- 12. При каких значениях x выполняется неравенство f’(x)
- 13. Определите при каких значениях переменной х верно равенство f’(x)=g’(x):Если даны функции:F(x)=2cosxG(x)=√3 x+7Ответ
- 14. При каких значениях х верно равенство f’(x)=g’(x):Если
- 15. В каких точках непрерывны функции:А) многочлен P(x)=a0xn+a1xn-1+…+an-1x+an;Б) дробно-рациональная?Ответ
- 16. Решите методом интервала неравенство:А) (x-2)(x+3)>0 Б) (x-2)(x+3)≤0В) x+2/x-1≥0Г) (x-1)(x+2)(x-3) (x+4)
- 17. Найдите тангенс угла наклона касательной к графику
- 18. В какой точке касательная к графику функции y=-x2+4x-3 параллельна оси абсцисс?Ответ
- 19. Движение точки происходит по закону s(t)=t2-4t+2. в какой момент времени скорость движения равна:А) 0Б) 6Ответ
- 20. Найдите скорость и ускорение в указанный момент
- 21. Две материальные точки движутся прямолинейно по законам:
- 22. Известно что тело массой m=5 кг движется
- 23. Знак производной f’(x) меняется по схеме, изображенной
- 24. На рисунке изображен график дифференцируемой функции y=h(x).
- 25. Опишите последовательность операций, которые нужно выполнить при отыскании промежутков возрастания (убывания) функции.Ответ
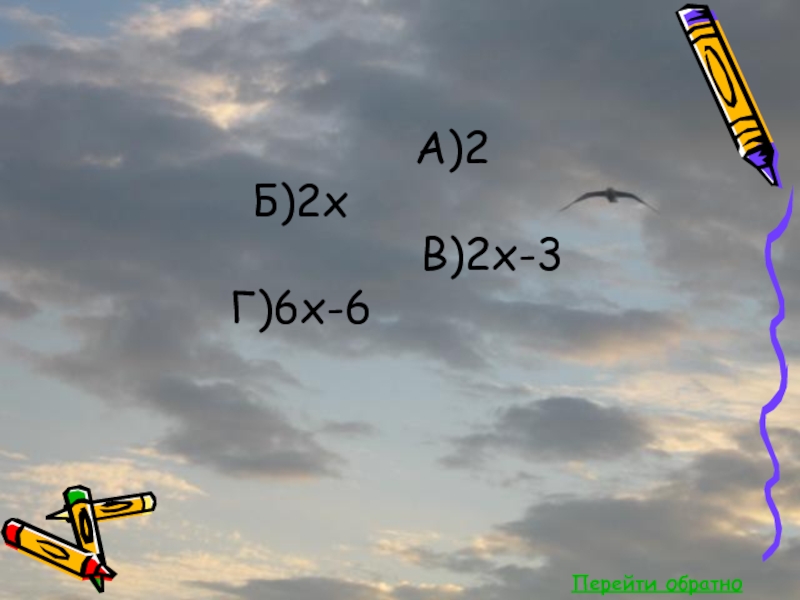
- 26. Найдите промежутки возрастания (убывания) функции:А) y=2x-3Б) y=3-2xВ) y=(x-1)2Г) y=-4x2-4x-1Ответ
- 27. На каких промежутках функции f(x) и g(x)
- 28. При каких значениях переменной x функция, графики
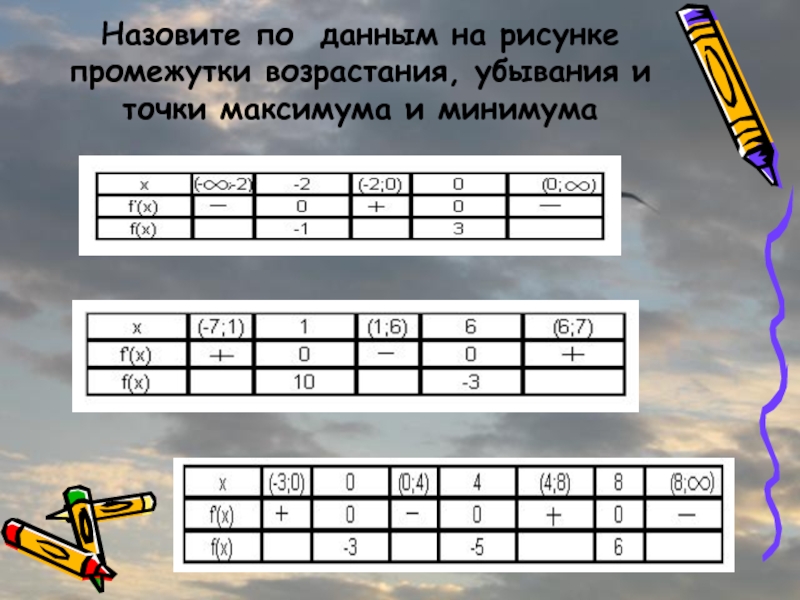
- 29. Назовите по данным на рисунке промежутки возрастания, убывания и точки максимума и минимума
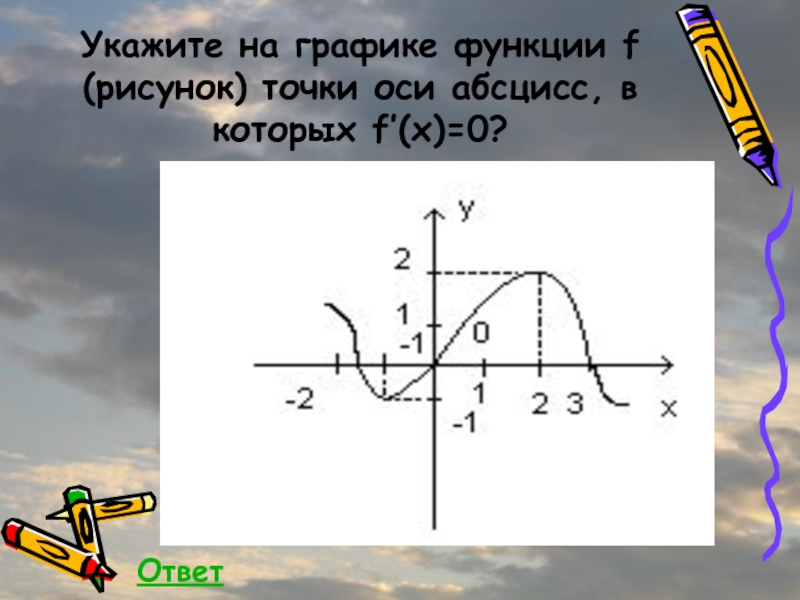
- 30. Укажите на графике функции f (рисунок) точки оси абсцисс, в которых f’(x)=0?Ответ
- 31. Исследуйте функцию на экстремум:А) f(x)=x2+2x-3Б) f(x)=-4x2-6x-7В) f(x)=3+4x-x2Г) f(x)=x2+x-2Ответ
- 32. Известно, что на отрезке [a;b] (в области
- 33. Назовите амплитуду, начальную фазу и угловую частоту
- 34. Найдите какое-нибудь отличное от нуля решение дифференциального уравнения:А) y’’=-36yБ) y’’=-1/49yВ) y’’=-yГ) y’’=-6yОтвет
- 35. выход
- 36. Перейти обратноА) 0.4 и 0.5 Б) 0.2 и 0.3 В) 1.7 и 1.8
- 37. Перейти обратно
- 38. Перейти обратно
- 39. Перейти обратно
- 40. Перейти обратно
- 41. Перейти обратноА) 6x2-9 cos3x Б)1/2√ (x-2)-2x sin(x2-2)
- 42. Перейти обратноА) 4/cos24x
- 43. Перейти обратно
- 44. Перейти обратноА) f’(0)>g’(π/2) Б) f’(π/4)>g’(π/3)
- 45. Перейти обратнопри любых значениях х
- 46. Перейти обратно(-1)n+1 π/3+πn,nєZ
- 47. Перейти обратноπn, nєZ
- 48. Перейти обратноА) многочлен не прерывен на всей
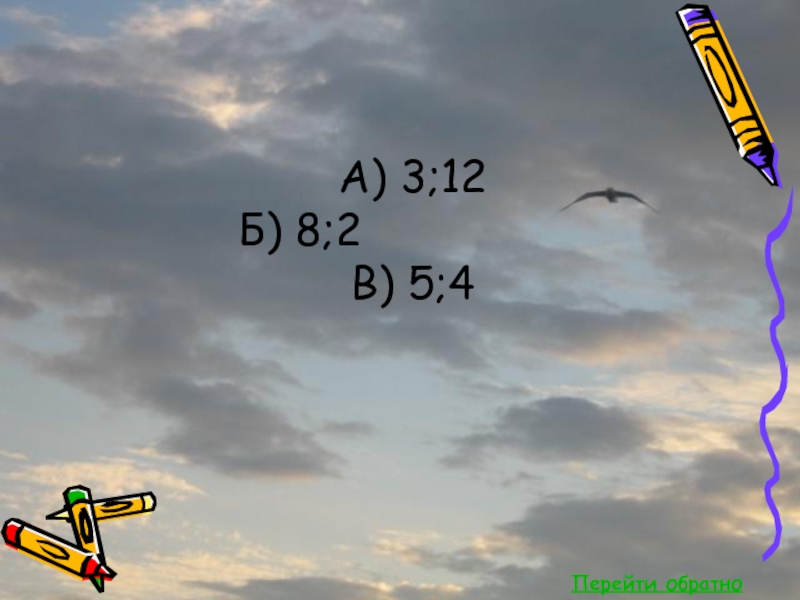
- 49. Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3)
- 50. Перейти обратно
- 51. Перейти обратно(2;0)
- 52. Перейти обратно А) t=2 Б) t=5
- 53. Перейти обратно
- 54. Перейти обратно2с.
- 55. Перейти обратно40 Дж
- 56. Перейти обратнофункция убывает на промежутках (-∞;-6], [0;1)
- 57. Перейти обратно
- 58. Перейти обратноНайти область определения функции Найти производную
- 59. Перейти обратноА)возрастает на (-∞; ∞) Б)убывает на
- 60. Перейти обратноА) функция f возрастает на [2;∞),
- 61. Перейти обратноА) x=-2 –точки минимума, x=2 –точка
- 62. Перейти обратнох=-1, х=2
- 63. Перейти обратноА) x=-1- точка минимума Б) x=-3/4
- 64. Перейти обратно-3;5
- 65. Перейти обратноА)0,3;3π/2;2 Б) 2;0;1 В) 1;0;5 Г) 1;0;6; Д) 1;π/3;3
- 66. Перейти обратноА) y=3,2 cos(6t+π/4) Б) y=4cos(1/7t+π) В) y=7,5 cos(t+1) Г) y=3,7 cos(√6 t+π/7)
- 67. Скачать презентанцию
Под темы:ПроизводнаяПрименение производной к приближенным вычислениям в геометрии и физикеПрименения производной к исследованию функций
Слайды и текст этой презентации
Слайд 2Под темы:
Производная
Применение производной к приближенным вычислениям в геометрии и физике
Применения
производной к исследованию функций
Слайд 3Найдите десятичные приближение чисел по недостатку и по избытку с
точностью до 0.1 :
Примеры:
А) 3/7
Б) 3/11
В) 17/9
Ответы
Слайд 4Найдите предел, к которому х→ 3 стремится функция, при lim
ƒ (х)=2;
lim g(х)=-3:
A) f(x) * g(x)
Б) 1/3g(x)
В) f3
(x) Г) (2f(х) + (3g (x))2
Д) 2 g(х)/ƒ(x)
Ответы
Слайд 5Найдите производные функции:
Примеры:
А) g(x)=2х-3
Б) g(x)=х2-2
В) g(x)=х2-3х+4
Г) g(x)=3х2-6х
Ответы
Слайд 6Найдите производную функции:
А) f(x)=(sin π /2-2x)3;
Б) f(x)=(2x cos 0+x2)2;
В) f(x)=(2x
sin π/6+1)2;
Г) f(x)=(2x2tg π/4-sin π)3
Ответы
Слайд 9Найдите производные функции:
А) h(x)=tgx+tg3x/1-tgx*tg3x
Б) h(x)=cos24x+sin24x
В)h(x)=1-cos2x/sinx
Ответы
Слайд 11Сравните значения выражений:
А) f’(0) и g’(π/2)
Б) f’(π/4) и g’(π/3)
если
f(x)=tgx и
g(x)=ctgx
Ответы
Слайд 13Определите при каких значениях переменной х верно равенство f’(x)=g’(x):
Если даны
функции:
F(x)=2cosx
G(x)=√3 x+7
Ответ
Слайд 14При каких значениях х верно равенство f’(x)=g’(x):
Если
f(x)=sin2x
g(x)=2x+3
Ответ
перейти на:
под темы
Слайд 15В каких точках непрерывны функции:
А) многочлен P(x)=a0xn+a1xn-1+…+an-1x+an;
Б) дробно-рациональная?
Ответ
Слайд 16Решите методом интервала неравенство:
А) (x-2)(x+3)>0
Б) (x-2)(x+3)≤0
В) x+2/x-1≥0
Г) (x-1)(x+2)(x-3) (x+4)
Слайд 17Найдите тангенс угла наклона касательной к графику функции в точке
с абсциссой x0
А)f(x)=2 sinx cosx, X0= π/2
Б)f(x)=2+tg(x+ π/6),x0= π/6
В) а(x)=3-ctgx,
x0= π/2Ответ
Слайд 19Движение точки происходит по закону s(t)=t2-4t+2. в какой момент времени скорость
движения равна:
А) 0
Б) 6
Ответ
Слайд 20Найдите скорость и ускорение в указанный момент времени для точки,
движущейся прямолинейно по закону:
А) s(t)=2t3-3t, t=1
Б) s(t)=t2+2t+1, t=3
В) s(t)=2t2-3t+4,
t=2Ответ
Слайд 21Две материальные точки движутся прямолинейно по законам: s1(t)=2.5t2-6t+1? S2(t)=0.5t2+2t-3 (t-время
в секундах, s-путь в метрах).в какой момент времени скорость первой
точки в два раза больше скорости второй?Ответ
Слайд 22Известно что тело массой m=5 кг движется прямолинейно по закону
s(t)=t2+2 (s-путь в метрах, t-время в секундах). Найдите кинетическую энергию
тела через 2с после начала движения.Ответ перейти на:
под темы
Слайд 23Знак производной f’(x) меняется по схеме, изображенной на рисунке. определите,
на каких промежутках функция возрастает и на каких убывает.
Ответ
Слайд 24На рисунке изображен график дифференцируемой функции y=h(x). Определите знак производной
функции на промежутках:
А) [-5;-2)
Б) (-2;3)
В) (3;5]
Ответ
Слайд 25Опишите последовательность операций, которые нужно выполнить при отыскании промежутков возрастания
(убывания) функции.
Ответ
Слайд 26Найдите промежутки возрастания (убывания) функции:
А) y=2x-3
Б) y=3-2x
В) y=(x-1)2
Г) y=-4x2-4x-1
Ответ
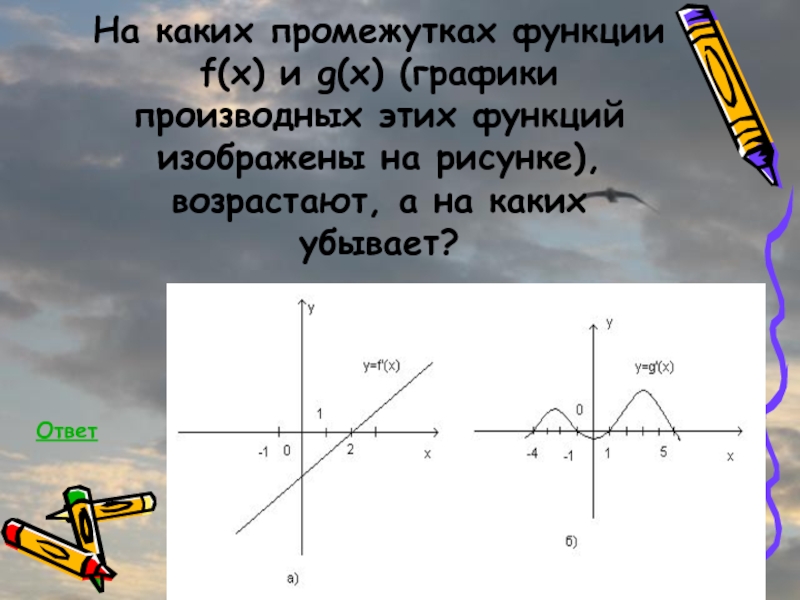
Слайд 27На каких промежутках функции f(x) и g(x) (графики производных этих
функций изображены на рисунке), возрастают, а на каких убывает?
Ответ
Слайд 28При каких значениях переменной x функция, графики производных которых изображены
на рисунке, имеют точки максимума и минимума?
Ответ
Слайд 31Исследуйте функцию на экстремум:
А) f(x)=x2+2x-3
Б) f(x)=-4x2-6x-7
В) f(x)=3+4x-x2
Г) f(x)=x2+x-2
Ответ
Слайд 32Известно, что на отрезке [a;b] (в области определения) функция f
имеет максимумы, равные 2 и 5, и минимум, равный 1,
f(a)=-3, f(b)=0. Чему равно наименьшее и наибольшее значения функции?Ответ
Слайд 33Назовите амплитуду, начальную фазу и угловую частоту колебания, преобразовав правую
часть к виду Acos(ωt+φ):
А) x(t)=0,3 cos(2t-π/2);
Б) x(t)=2 cos t
В) x(t)=cos2t
cos3t-sin2t sin3tГ) x(t)=cos8t cos2t+sin8t sin2t
Д) x(t)=cosπ/3 cos3t-sinπ/3 sin3t
Ответ
Слайд 34Найдите какое-нибудь отличное от нуля решение дифференциального уравнения:
А) y’’=-36y
Б) y’’=-1/49y
В)
y’’=-y
Г) y’’=-6y
Ответ
Слайд 48Перейти обратно
А) многочлен не прерывен на всей числовой прямой
Б) дробно-рациональная
функция непрерывна во всех точках своей области определения
Слайд 56Перейти обратно
функция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция
возрастает на [-6;0] и [3; ∞).
Слайд 58Перейти обратно
Найти область определения функции
Найти производную заданной функции
Найти значения независимой
переменной, при которых значение производной положительны (отрицательны) Записать промежутки возрастания (убывания)
функцииСлайд 59Перейти обратно
А)возрастает на (-∞; ∞)
Б)убывает на (-∞;∞)
В)убывает на (-∞;1], возрастает
на [1;∞)
Г)возрастает на (-∞;-1/2], убывает на [-1/2;)
Слайд 60Перейти обратно
А) функция f возрастает на [2;∞), убывает на (∞;2]
Б)
функция g убывает на (-∞;-4], [1;1] и [5;∞);
возрастает на [-4;-1] и [1;5]Слайд 61Перейти обратно
А) x=-2 –точки минимума, x=2 –точка максимума
Б) x=-1, x=3
– точки минимума, x=-4, x=1 –точки максимума
В) x=2 –точка максимума
Слайд 63Перейти обратно
А) x=-1- точка минимума
Б) x=-3/4 –точка максимума
В) x=2 –точка
максимума
Г) x=-1/2 –точка минимума
Слайд 66Перейти обратно
А) y=3,2 cos(6t+π/4)
Б) y=4cos(1/7t+π)
В) y=7,5 cos(t+1)
Г) y=3,7 cos(√6 t+π/7)
Теги























![Производная и её применение На рисунке изображен график дифференцируемой функции y=h(x). Определите знак производной функции На рисунке изображен график дифференцируемой функции y=h(x). Определите знак производной функции на промежутках: А) [-5;-2)Б) (-2;3)В) (3;5]Ответ](/img/tmb/1/65863/5beeb23b6375f27fe357759235457d5b-800x.jpg)




![Производная и её применение Известно, что на отрезке [a;b] (в области определения) функция f имеет Известно, что на отрезке [a;b] (в области определения) функция f имеет максимумы, равные 2 и 5, и](/img/tmb/1/65863/a9190c23dd1fdeafa57a0231997d0390-800x.jpg)





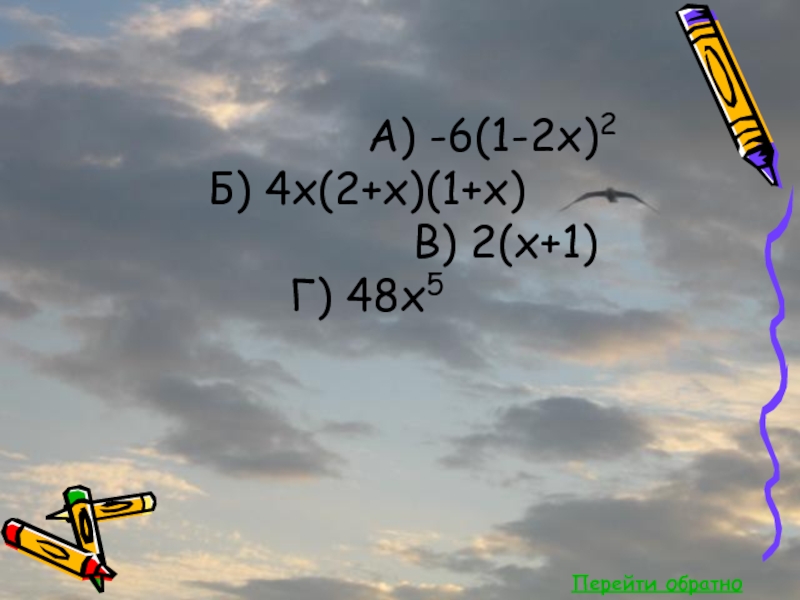
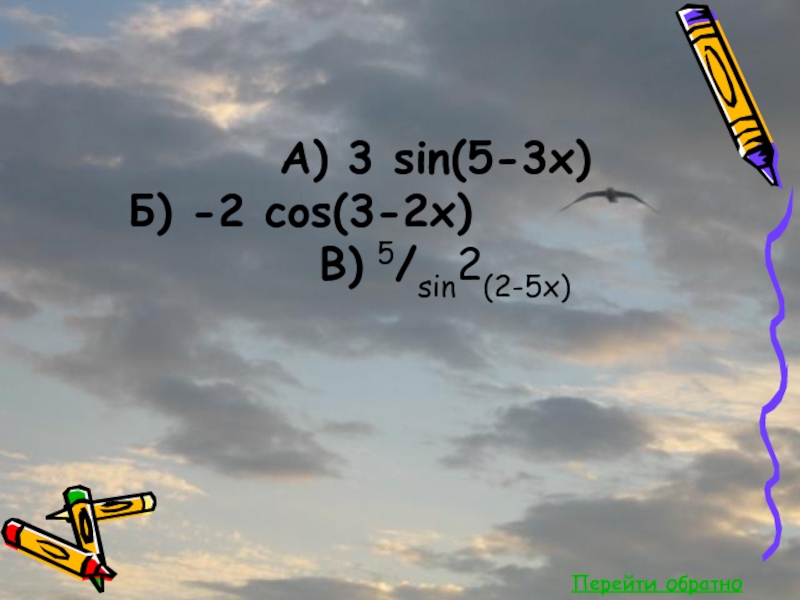
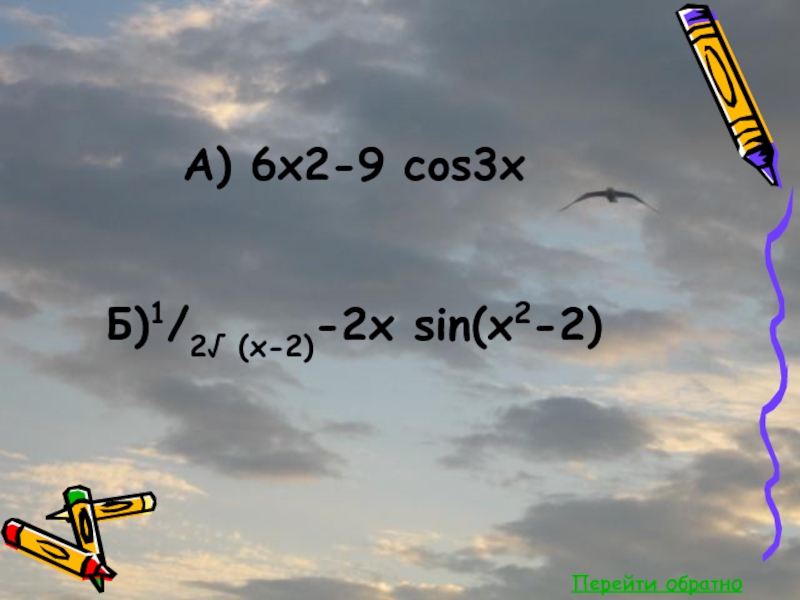
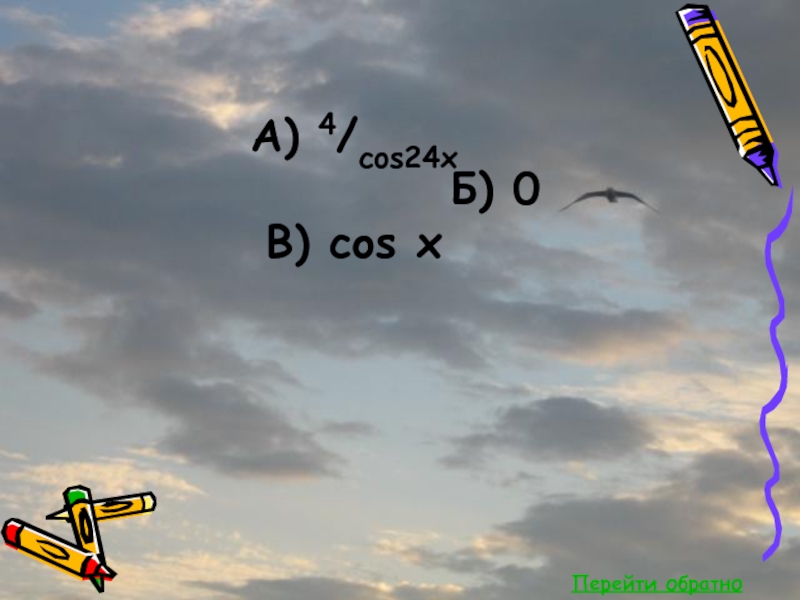

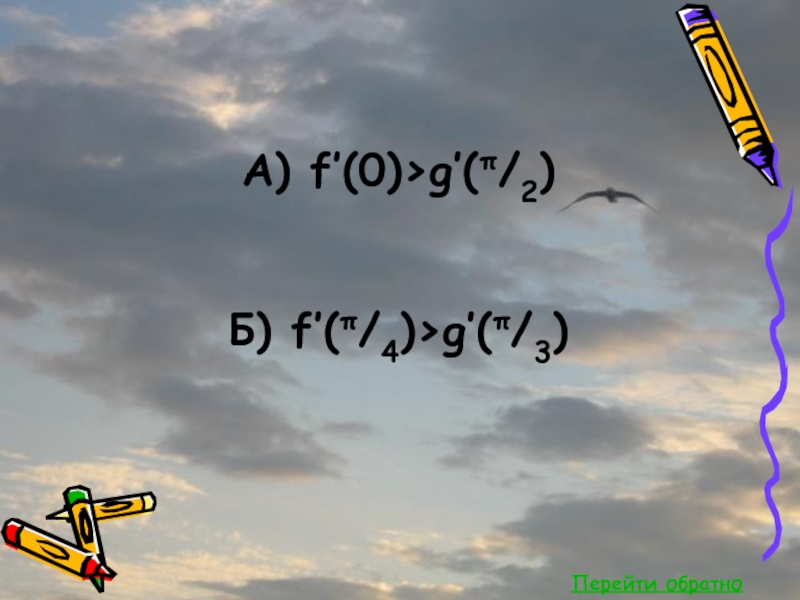

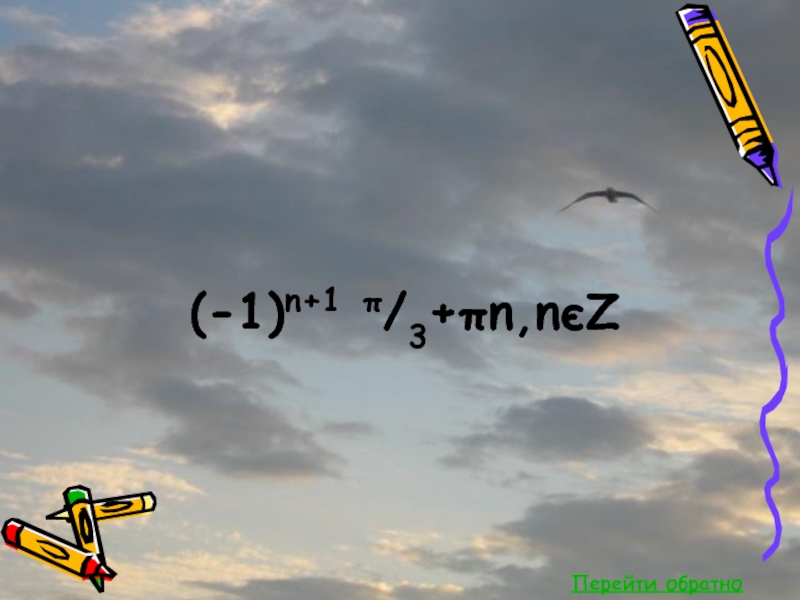


![Производная и её применение Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3) Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3)](/img/tmb/1/65863/733a8f9130284a87cbb79284110b1e72-800x.jpg)





![Производная и её применение Перейти обратнофункция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция возрастает Перейти обратнофункция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция возрастает на [-6;0] и [3; ∞).](/img/tmb/1/65863/213fc05509bb0663dbfd41c2619f3ac4-800x.jpg)


![Производная и её применение Перейти обратноА)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1], Перейти обратноА)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1], возрастает на [1;∞) Г)возрастает на (-∞;-1/2],](/img/thumbs/e1d3a0b3c7897ab53b0e6b3e08ed2fc2-800x.jpg)
![Производная и её применение Перейти обратноА) функция f возрастает на [2;∞), убывает на (∞;2] Б) Перейти обратноА) функция f возрастает на [2;∞), убывает на (∞;2] Б) функция g убывает на (-∞;-4],](/img/thumbs/7ec4c16f740b943e894cd1d2beda7016-800x.jpg)