Простейшие вероятностные задачи. Элементарные и сложные события. Вероятность противоположного события 11 класс

из тех 25 билетов, которые будут предложены на экзамене. Какова

вероятность того, что студенту достанется на экзамене выученный билет?

Задача №1

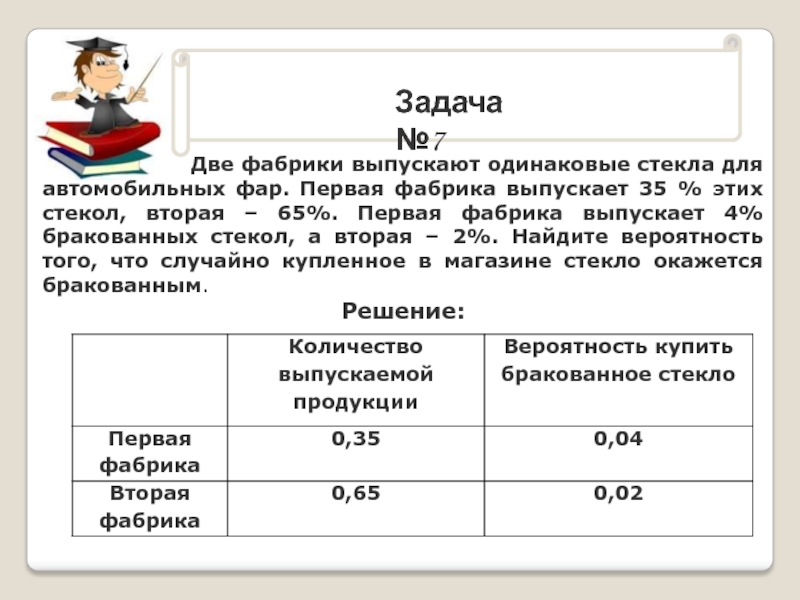
Решение:

N = 25 – количество билетов
N(A) = 25-1 = 24 – количество выученных билетов
P(A)= 24/25 = 0,96 – искомая вероятность.
Ответ: 0,96.

Элементарные и сложные события. Вероятность противоположного события »

то, относительно чего после некоторого момента времени можно сказать одно

и только одно из двух. Да, оно произошло. Нет, оно не произошло.

оно обязательно произойдет в
результате

данного испытания.

Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.

Событие называется невозможным,
если оно не
может произойти
в результате
данного испытания.

эксперимента, называется элементарным событием, а множество таких исходов называется просто

событием.

Из урны наудачу берут один шар. Извлечение шара из урны есть испытание.
Появление шара определенного цвета – событие.

Единичное случайное событие происходит единожды, например, падение Тунгусского метеорита.
Теория вероятностей изучает только массовые события.

которые не могут произойти одновременно.

Равновозможные события – это такие

события, каждое из которых не имеет никаких преимуществ в появлении чаще, чем другое, во время многоразовых испытаний, которые проводятся при одинаковых условиях.

Вероятностью события Р(А) – называется отношение числа благоприятных исходов N(A) к числу всех возможных исходов N :

данного испытания.
2) Найти количество N(A) тех исходов, в которых

наступает событие А .

Вычислить частное, которое будет равно
вероятности события А.

Вероятность события:

вверх две правильные монеты упадут на

одну и ту же сторону?

Решение, предложенное Даламбером:

Опыт имеет три равновозможных исхода:

1)Обе монеты упали на «орла».
2)Обе монеты упали на «решку».
3)Одна из монет упала на «орла»,
другая на «решку».

N = 3; N(A) = 2; P(A) = 2/3

.

один. Природа различает все предметы!!!

Орел, орел
Решка, решка
Орел, решка
Решка, орел
N =

4; N(A) = 2; P(A) = 1/2

.

соответствует единственному исходу из N
равновозможных) равна 1/N.

2)Вероятность невозможного события равна 0.
3)Вероятность достоверного события равна 1.
4) Вероятность любого события заключена в пределах от
0 до 1: 0  Р(А)  1.
5) Вероятность события, противоположного событию А
(события, заключающегося в том , что событие А не
наступает), равна 1- Р(А).

и В называют событие А*В, состоящее в наступлении обоих этих

событий

Если события А и В независимы (они происходят в разных испытаниях, и исход одного испытания не может влиять на исход другого), то вероятность того, что наступят оба этих события, равна Р(А)*Р(В):
Р(А*В)=Р(А)*Р(В)
Например, вероятность выпадения двух шестерок при двукратном бросании кубика равна: 1/6*1/6=1/36.

суммы событий
.

Суммой событий А и В называют событие А+В, состоящее в наступлении хотя бы одного из этих событий.

Если А и В несовместны, то Р(А+В)=Р(А)+Р(В)

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события:

на 80 качественных сумок приходится 8 сумок со скрытыми дефектами.

Найдите вероятность того, что купленная сумка окажется качественной.

Решение:

N(A) = 80
N= 80+8=88
P(A) = 80/88 = 0,91
Ответ: 0,91.

180  сумок восемь сумок со скрытыми дефектами. Найдите вероятность того,

что купленная сумка окажется качественной. Результат округлите до сотых.

Решение:

N(A) = 180-8 = 172 сумки качественные,
N = 180 всего сумок

P(A) = 172/180 = 0,955...≈ 0,96

Ответ: 0,96.

по бадминтону участников разбивают на игровые пары случайным образом с

помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

Решение:
Так как Руслан Орлов сам с собой играть не может, то вероятность его игры с каким-нибудь спортсменом из России будет (N(A)=9, N=25):
P(A) = 9/25 = 0,36.

В таблице приведены результаты диагностической работы по математике в

9-х классах. Какова вероятность того, что оценка выбранной наугад работы будет выше, чем среднее по школе значение оценки?

Решение:
7+20+15+8 = 50 – всего учащихся
(2*7+3*20+4*15+5*8):50 = 3,48 ≈ 3 – среднее по школе значение оценки.
15+8=23 – количество девятиклассников, получивших оценку выше средней по школе. Р = 23/50 = 0,46.
Ответ: 0,46.

Ваня забыл последние 2 цифры пароля для

входа на сайт, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.

Решение:
Подсчитаем количество всех возможных двузначных чисел с разными цифрами, меньшее 30, которые может набрать абонент:

Таких чисел 18. Так как только одно число правильное, то искомая вероятность Р=1/18. Ответ: 1/18.

Две фабрики выпускают одинаковые стекла для автомобильных фар.

Первая фабрика выпускает 35 % этих стекол, вторая – 65%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:

Вероятность того, что бракованное стекло куплено на первой

фабрике  равна 0,35∙0,04 = 0,0140.
Вероятность того, что бракованное текло куплено на второй фабрике равна  0,65∙0,02 = 0,0130.
Так как это независимые события, то полученные вероятности складываем: 0,0140 + 0,0130 = 0,027

Ответ: 0,027

«Теория вероятностей – не что иное,

как здоровый смысл, подкрепленный вычислениями». (Маркиз де Лаплас)

«Истинная логика нашего мира – правильный подсчет вероятностей». (Джеймс Максвелл)

Блез Паскаль
Французский физик , математик , философ
(1623 –

1662)

которого не сомневаются
Какова вероятность невозможного события?
Какова вероятность достоверного

события?
В каких пределах находится вероятность?
Как называются два события, имеющие одинаковую вероятность?
Вероятность случайного события равна …
События А и В называются несовместными, если …
Вероятность события, противоположного событию А равна…
Суммой событий А и В называют событие …
Произведением событий А и В называют событие …

режиме онлайн - тренировки по адресу:
http://ege.yandex.ru/mathematics/

могу…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал

мне для жизни…

Подведем итоги

Одним предложением, выбирая начало фразы из предложенного списка, подведите итог нашего урока.