Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Trigonometry (Sum and Differece Formulas)
Содержание
- 1. Trigonometry (Sum and Differece Formulas)
- 2. The students will learn Introduction trigonometric ratios
- 3. Trigonometric Ratios of The Sum or Difference of Two ArcsTheorem 1.4Theorem 1.5Theorem 1.6Theorem 1.7
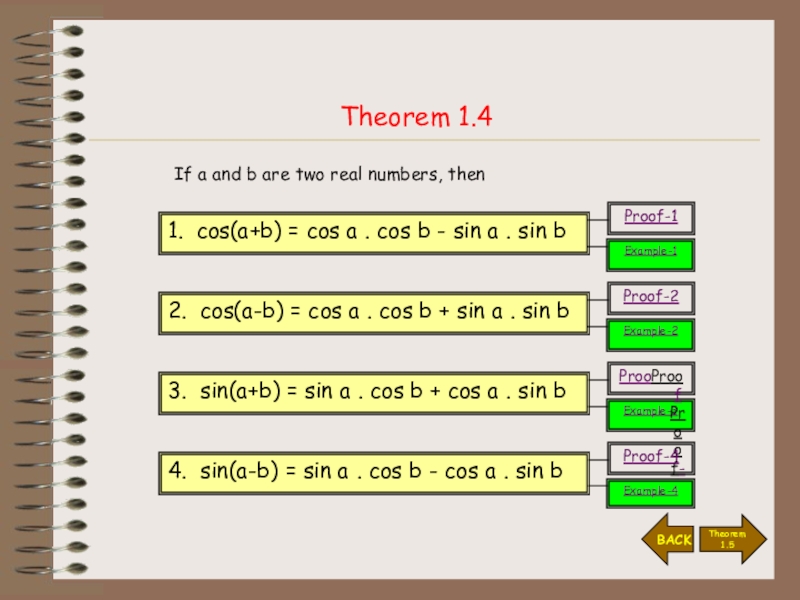
- 4. Theorem 1.4If a and b are two real numbers, thenTheorem 1.5BACK
- 5. Proof-1 cos(a+b) = cos a . cos
- 6. Full screenBACK
- 7. Example-1:Solution-1cos 75o = ?
- 8. Solution-1:cos 75º = cos ( 45º +
- 9. Proof-2 cos(a-b) = cos a .
- 10. Example-2:Solution-2cos 15o = ?
- 11. Solution-2:cos 15º = cos ( 45º -
- 12. Proof-3 sin(a+b) = sin a .
- 13. Example-3:Solution-3sin 105o = ?
- 14. Solution-3:sin 105º = cos ( 60º +
- 15. Proof-4 sin(a+b) = sin a .
- 16. Example-4:Solution-4sin 15o = ?
- 17. Solution-4:sin 15º = cos ( 60º -
- 18. Theorem 1.51. If a, b and a+b
- 19. Proof-5BACKExample-5
- 20. Example-5:Solution-5Let α and β be two acute
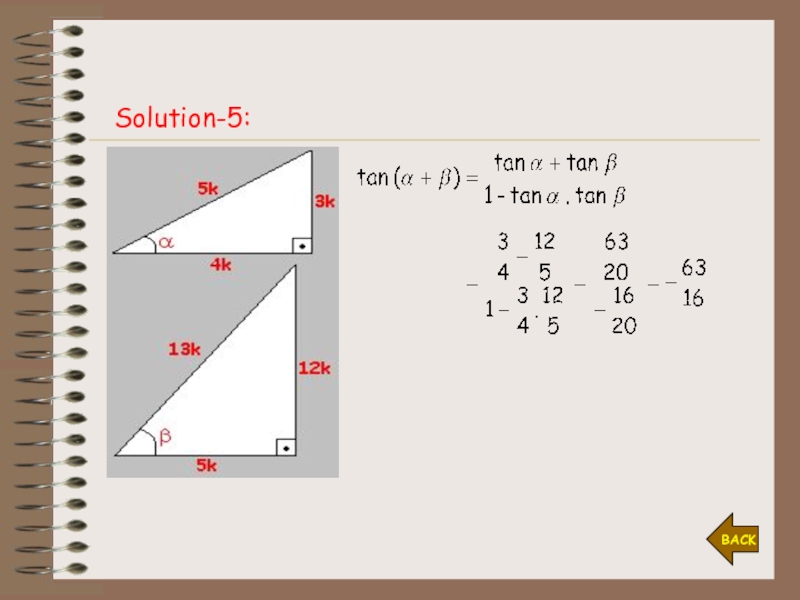
- 21. Solution-5:BACK
- 22. Proof-62. If we write –b instead of b in the previous equality then,BACKExample-6
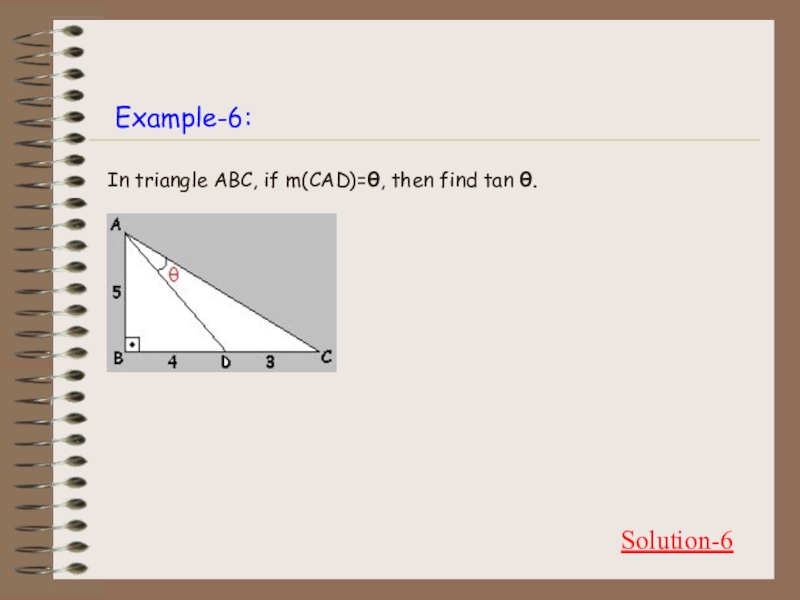
- 23. Example-6:Solution-6In triangle ABC, if m(CAD)=θ, then find tan θ.
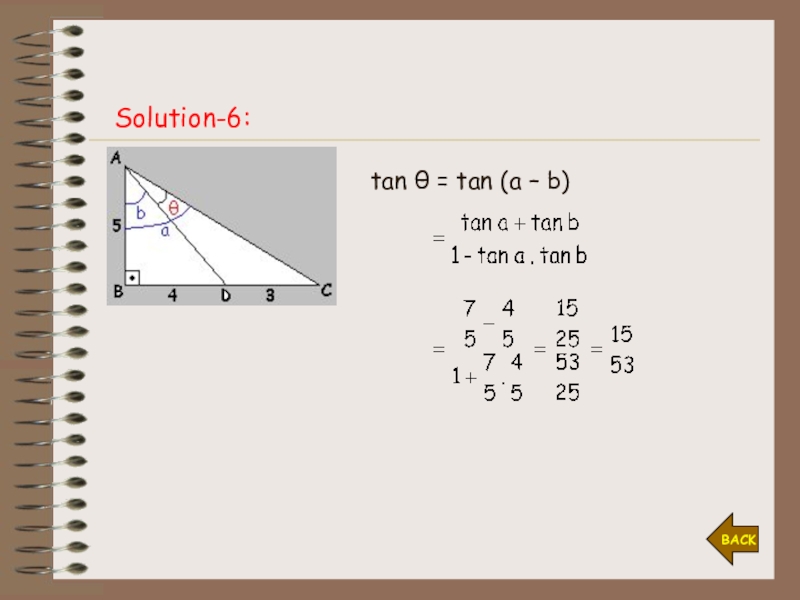
- 24. Solution-6:BACKtan θ = tan (a – b)
- 25. Theorem 1.61. If a, b and a+b
- 26. Proof-7BACKExample-7
- 27. Example-7:Solution-7In the adjoining figure ⏐AB⏐= 4, ⏐BC⏐=
- 28. Solution-7:BACK⏐AC⏐ = 5 and ⏐CD⏐ = 13.
- 29. Proof-82. If we write –b instead of b in the previous equality then,BACKExample-8
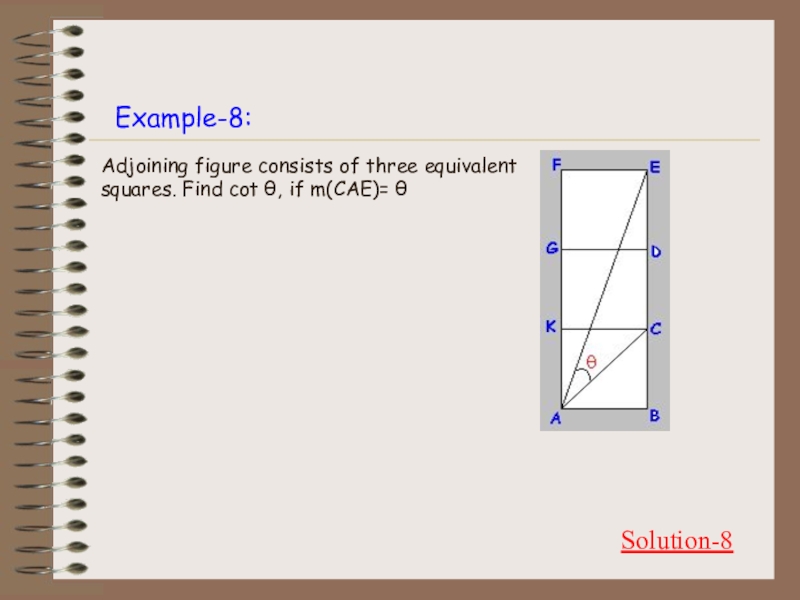
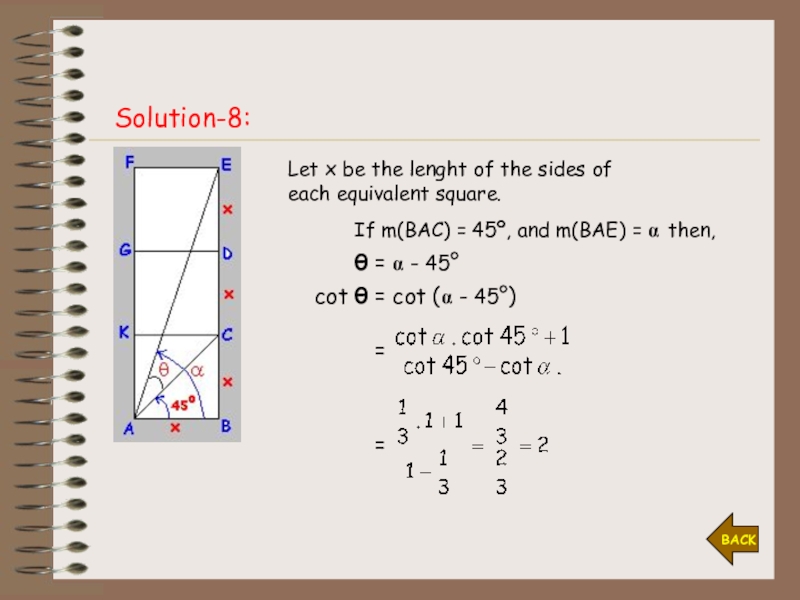
- 30. Example-8:Solution-8Adjoining figure consists of three equivalent squares. Find cot θ, if m(CAE)= θ
- 31. Solution-8:BACKLet x be the lenght of the
- 32. Theorem 1.71. If a, b and a+b
- 33. Скачать презентанцию
The students will learn Introduction trigonometric ratios of the sum or difference of two arcs, half-angle formulas, conversion and inverse conversion formulas.
Слайды и текст этой презентации
Слайд 2The students will learn
Introduction
trigonometric ratios of the sum
or difference of two arcs,
conversion formulas.
Слайд 3Trigonometric Ratios of
The Sum or Difference of Two Arcs
Theorem
1.4
Theorem 1.5
Theorem 1.6
Theorem 1.7
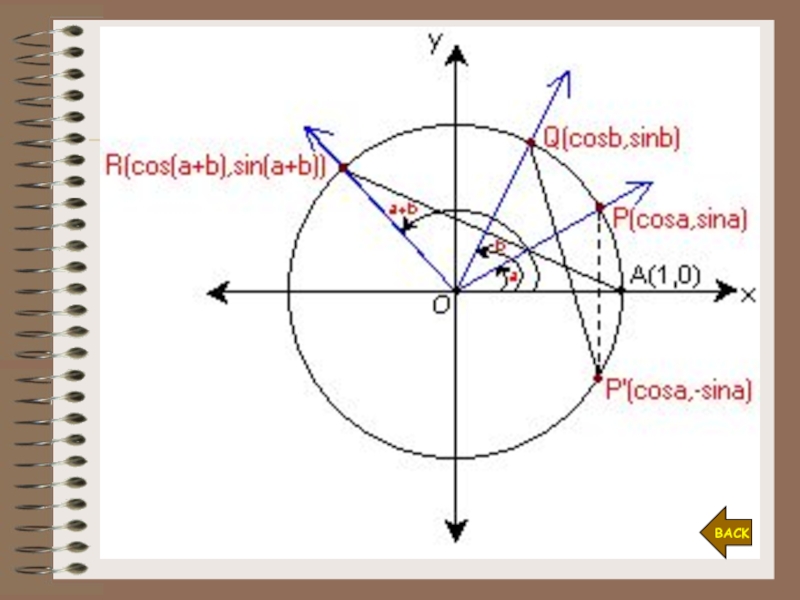
Слайд 5Proof-1 cos(a+b) = cos a . cos b - sin a
. sin b
Since the lenghts of arc AP and AP’
are equal then ⏐AR⏐=⏐P’Q⏐.If is the distance between two points (x1,y1) and (x2,y2),
then the distance formula will be as follows then
⏐AR⏐=⏐P’Q⏐⇒⏐AR⏐2=⏐P’Q⏐2
(cos(a+b)-1)2 + (sin(a+b)- 0)2 = (cos a – cos b)2 + (sin b + sin a)2
cos2(a+b) – 2cos(a+b) + 1 + sin2(a+b) = cos2a –2cosa.cosb + cos2b + sin2b + 2sina. sinb + sin2a
2 – 2cos(a+b) = 2 – 2cosa.cosb + 2sinb.sina
cos(a+b) = cosa. cosb – sina. sinb
Full Screen
BACK
Example-1
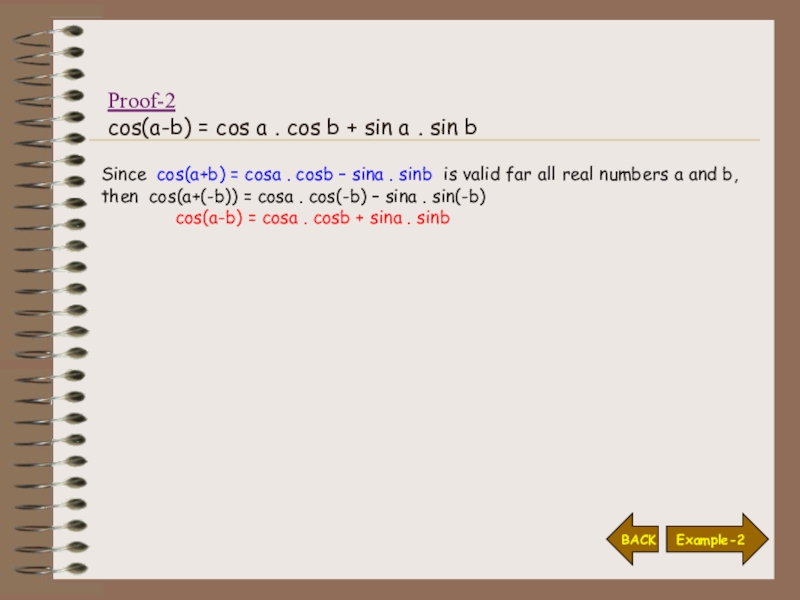
Слайд 9Proof-2 cos(a-b) = cos a . cos b + sin
a . sin b
Since cos(a+b) = cosa . cosb –
sina . sinb is valid far all real numbers a and b,then cos(a+(-b)) = cosa . cos(-b) – sina . sin(-b)
cos(a-b) = cosa . cosb + sina . sinb
BACK
Example-2
Слайд 12Proof-3 sin(a+b) = sin a . cos b + cos
a . sin b
We can write sine in terms of
cosine by using reduction formulas. Hence,sin(a+b) = sin a . cos b + cos a. sin b
BACK
Example-3
Слайд 15Proof-4 sin(a+b) = sin a . cos b - cos
a . sin b
Since the equality sin(a+b) = sin a
. cos b + cos a. sin b is valid for all real numbers a and b, by writing –b instead of b, we getsin(a+(-b)) = sin a . cos(-b) + cos a. sin(-b) then
sin(a+b) = sin a . cos b - cos a . sin b
BACK
Example-4
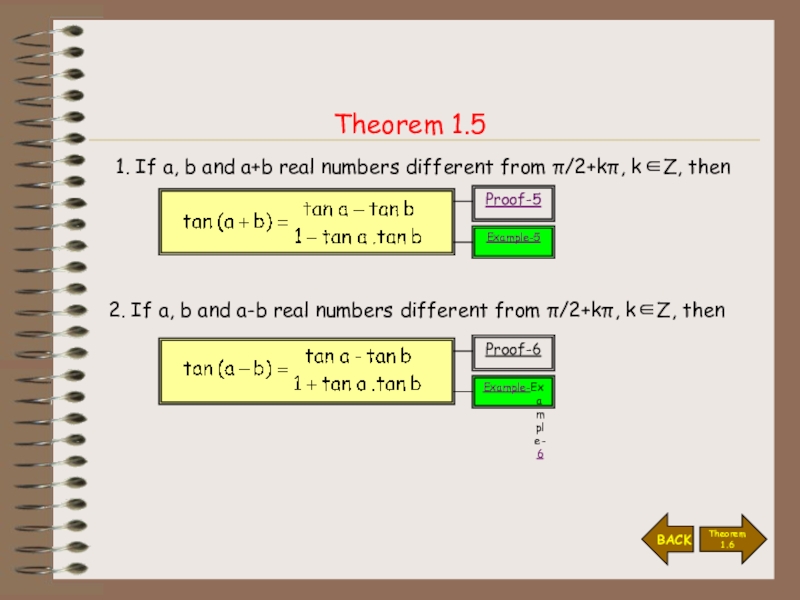
Слайд 18Theorem 1.5
1. If a, b and a+b real numbers different
from π/2+kπ, k∈Z, then
2. If a, b and a-b real
numbers different from π/2+kπ, k∈Z, thenProof-5
Example-5
Proof-6
Example-Example-6
Theorem 1.6
BACK
Слайд 20Example-5:
Solution-5
Let α and β be two acute angles.
If sin α=3/5
and cos β= 5/13, then find tan(α+β).
Слайд 25Theorem 1.6
1. If a, b and a+b real numbers different
from kπ, k∈Z, then
2. If a, b and a-b real
numbers different from kπ, k∈Z, thenTheorem 1.7
BACK
Слайд 27Example-7:
Solution-7
In the adjoining figure ⏐AB⏐= 4, ⏐BC⏐= 3, ⏐AD⏐= 12
and m(ABC)=90º, m(CAD)=90º, m(CED)=90º. Find cot θ, if m(DCE) =
θ .
Слайд 28Solution-7:
BACK
⏐AC⏐ = 5 and ⏐CD⏐ = 13.
Put m(ACB) =
a and m(ACD) = b then,
θ = 180° -
(a + b) cot θ = cot (180° - (a + b))
= - cot (a + b)
Слайд 30Example-8:
Solution-8
Adjoining figure consists of three equivalent squares. Find cot θ,
if m(CAE)= θ
Слайд 31Solution-8:
BACK
Let x be the lenght of the sides of each
equivalent square.
If m(BAC) = 45º, and m(BAE) = α then,
θ = α - 45°
cot θ = cot (α - 45°)
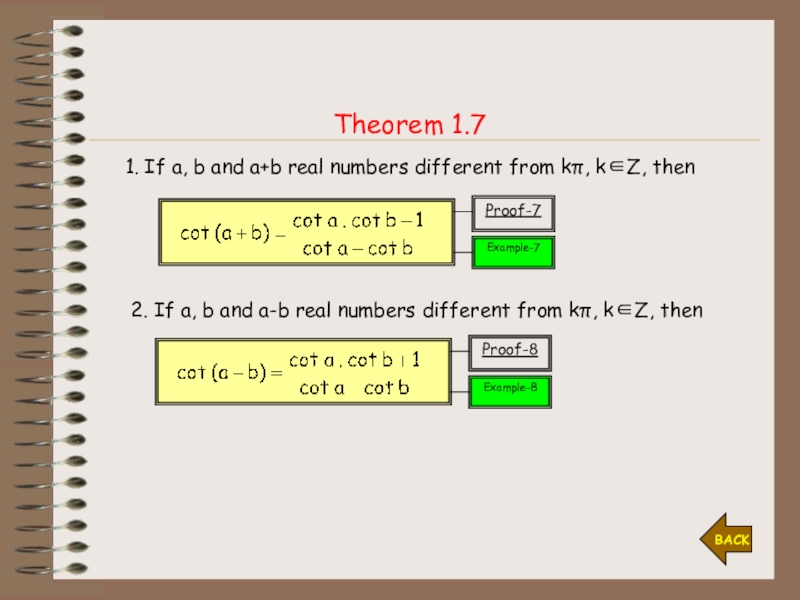
Слайд 32Theorem 1.7
1. If a, b and a+b real numbers different
from kπ, k∈Z, then
2. If a, b and a-b real
numbers different from kπ, k∈Z, thenBACK
