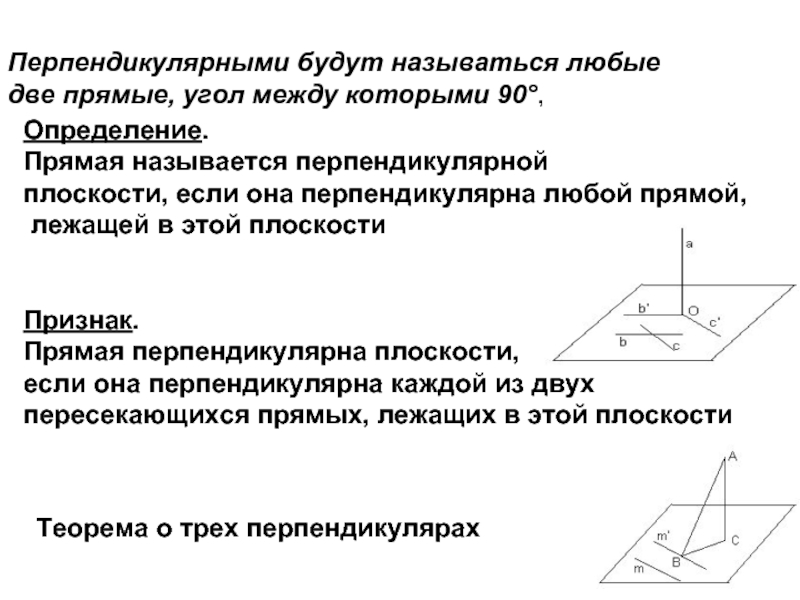
лучами, которые этим прямым
соответственно параллельны.
Следствия.
Если а || b,
то ∠(a; b) = 0°; Если а b = O, то ∠(a; b) – тот из образовавшихся
углов с вершиной О, который не тупой.
3) Если а ÷ b, то ∠(a; b) = ∠(a’; b’), где a’ || a; b’ || b; a’ b’ = O’.
Таким образом, 0° ≤ ∠(a; b) ≤ 90°.





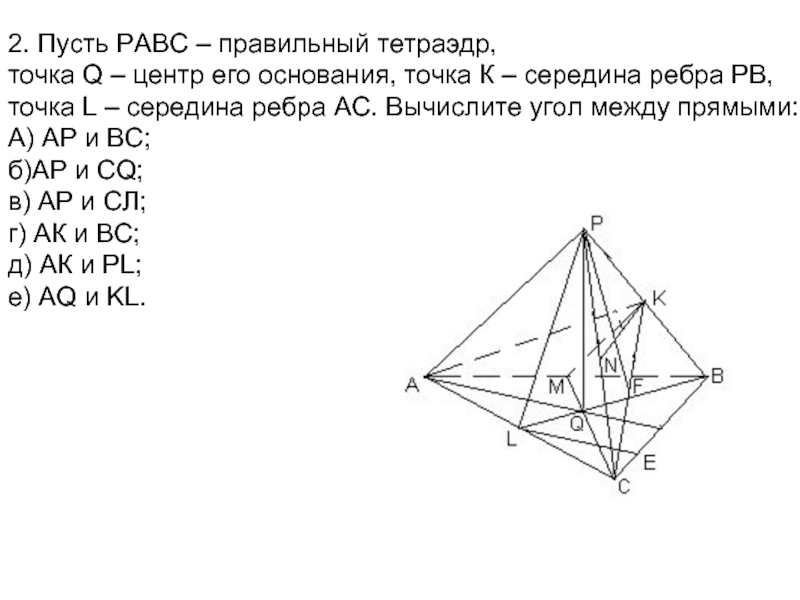
![РАССТОЯНИЯ МЕЖДУ ПРЯМЫМИ °; ; ; , ; ; , ; ] а) ∠((АР); °; ; ; , ; ; , ; ] а) ∠((АР); (ВС)) = 900б) ∠((АР); (СQ)) =](/img/thumbs/cf41e5989dbeae1b0552d398eb92bf57-800x.jpg)