Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разработка урока
Содержание
- 1. Разработка урока
- 2. Цели урока:выявить степень сформированности у учащихся понятия
- 3. Слайд 3
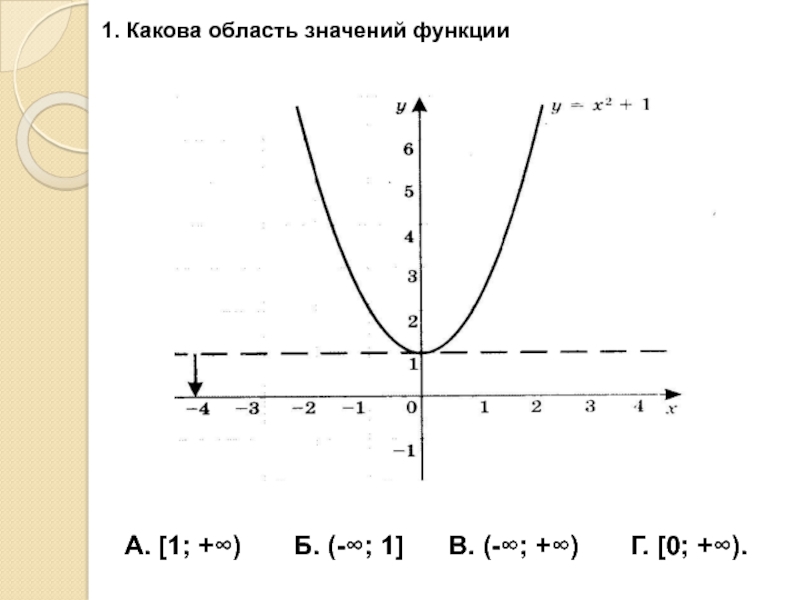
- 4. 1. Какова область значений функции
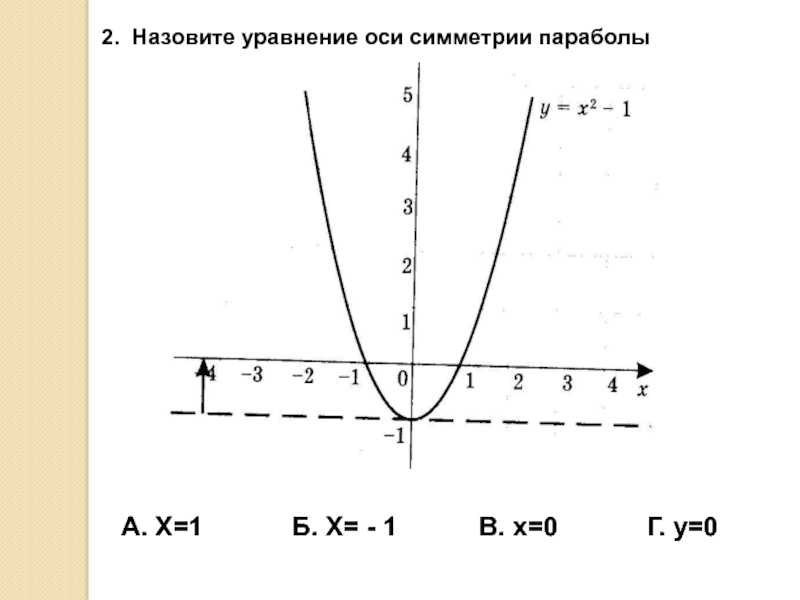
- 5. 2. Назовите уравнение оси симметрии параболы
- 6. 3. Назовите промежутки, в которых y >
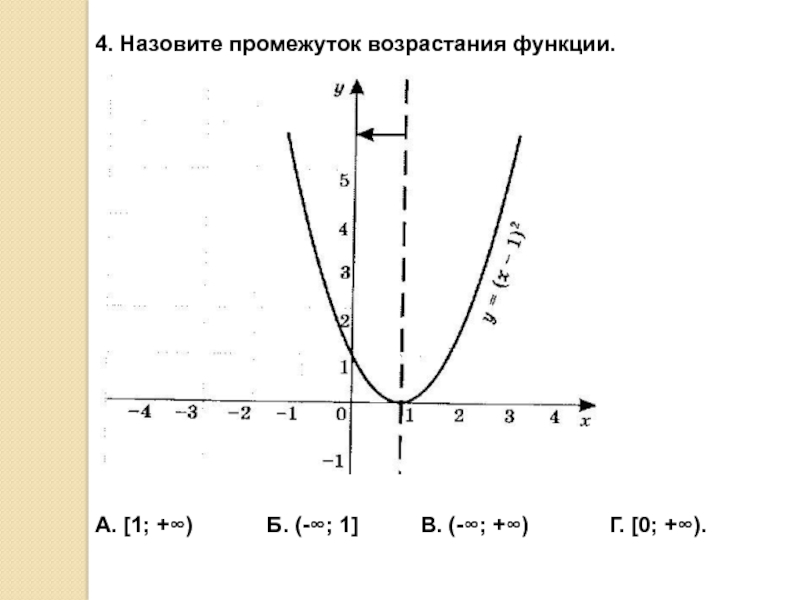
- 7. 4. Назовите промежуток возрастания функции.
- 8. 5. Укажите координаты вершины параболы, заданной формулой
- 9. 6. Через какую из указанных точек пройдёт
- 10. 7. С какой прямой график параболы y
- 11. 8. График какой функции изображён на рисунке?
- 12. 9. Найдите координаты вершины параболы у=2х2- 16х
- 13. 10.По рисунку определите знак коэффициента ɑ и
- 14. 1.Найдите координаты вершины параболы 2.Используя шаблон параболы
- 15. 4. Работа по учебнику: № 124 (б)
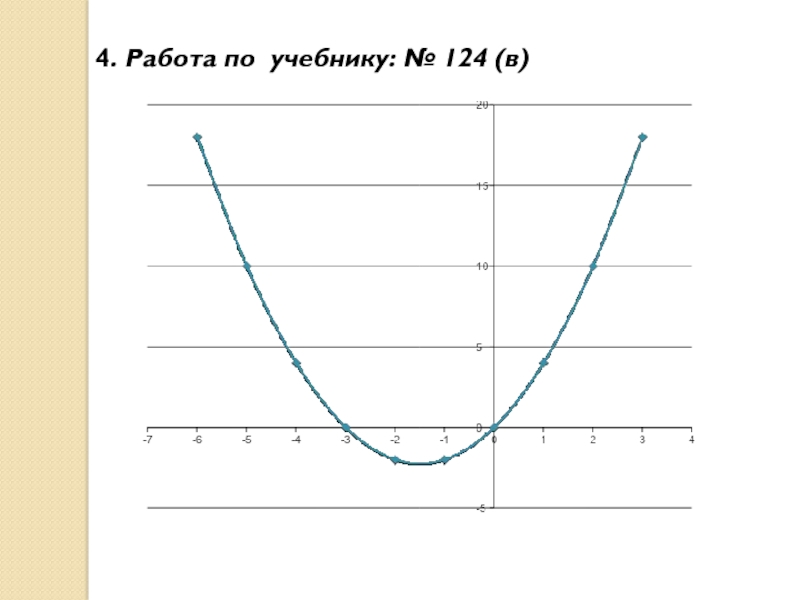
- 16. 4. Работа по учебнику: № 124 (в)
- 17. Ответы к самостоятельной работе.Вариант I 3
- 18. Домашнее задание.повторить свойства графика квадратичной функции, алгоритм
- 19. Спасибо за урок!
- 20. Скачать презентанцию
Цели урока:выявить степень сформированности у учащихся понятия квадратичной функции, её свойств, особенностей её графика; обобщить, закрепить и систематизировать знания по данной теме; создать условия для формирования умения анализировать, сравнивать, классифицировать графики
Слайды и текст этой презентации
Слайд 1«Квадратичная функция,
её свойства и график».
Разработан учителем математики МБОУ
«Моховицкая СОШ» Лавровой Т.И.
Слайд 2Цели урока:
выявить степень сформированности у учащихся понятия квадратичной функции, её
свойств, особенностей её графика;
обобщить, закрепить и систематизировать знания по
данной теме; создать условия для формирования умения анализировать, сравнивать, классифицировать графики квадратичных функций;
продолжить подготовки к итоговой аттестации;
воспитывать аккуратность при построении чертежей и работе на доске, умение работать в группе;
развивать вычислительные навыки и пространственное мышление учащихся, мыслительные операции.
Слайд 8
5. Укажите координаты вершины параболы, заданной формулой
y = (x + 2)2 - 1
А. (-2; -1) Б. (-2; 1) В. (2; -1) Г. (2; 1).
Слайд 96. Через какую из указанных точек пройдёт график квадратичной функции
y = f (x),
если его
продолжить в полуплоскость x>0?
А.(3;1) Б.(2;0) В. (5; -3) Г. (1; 5).
Слайд 107. С какой прямой график параболы y = -x2 +
4х – 3
не имеет общих точек?
A. y =
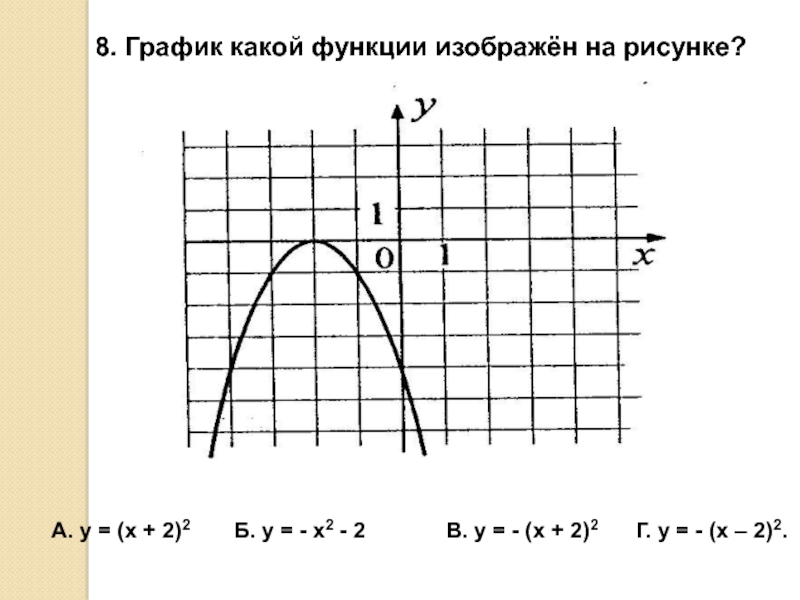
-10 Б. у = 1 В. у = 0 Г. у = 4 Слайд 118. График какой функции изображён на рисунке?
A. y = (x + 2)2 Б. y = - x2 - 2 В. y = - (x + 2)2 Г. y = - (x – 2)2.
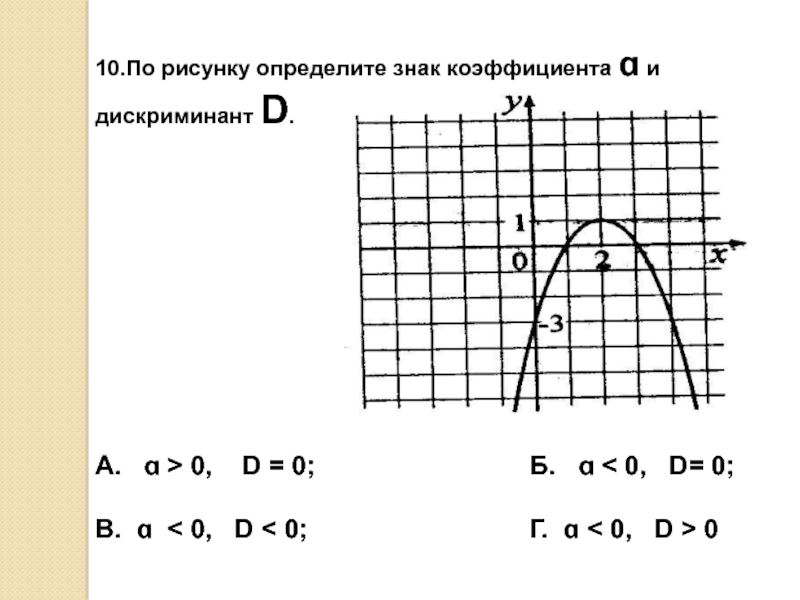
Слайд 1310.По рисунку определите знак коэффициента ɑ и дискриминант D.
А.
ɑ > 0, D = 0;
Б. ɑ < 0, D= 0;В. ɑ < 0, D < 0; Г. ɑ < 0, D > 0


![Разработка урока 3. Назовите промежутки, в которых y > 0. 3. Назовите промежутки, в которых y > 0. А. [-1;3]](/img/thumbs/00398e9510d2c8ab00a93348e0fa0fe6-800x.jpg)