Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рациональные неравенства
Содержание
- 1. Рациональные неравенства
- 2. Метод интервалов заключается в следующем: Числовая прямая
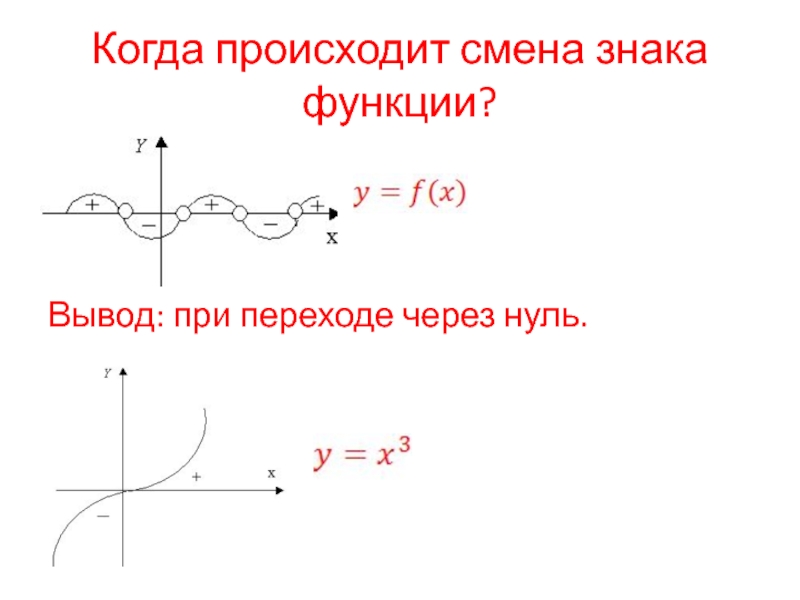
- 3. Когда происходит смена знака функции? Вывод: при переходе через нуль.
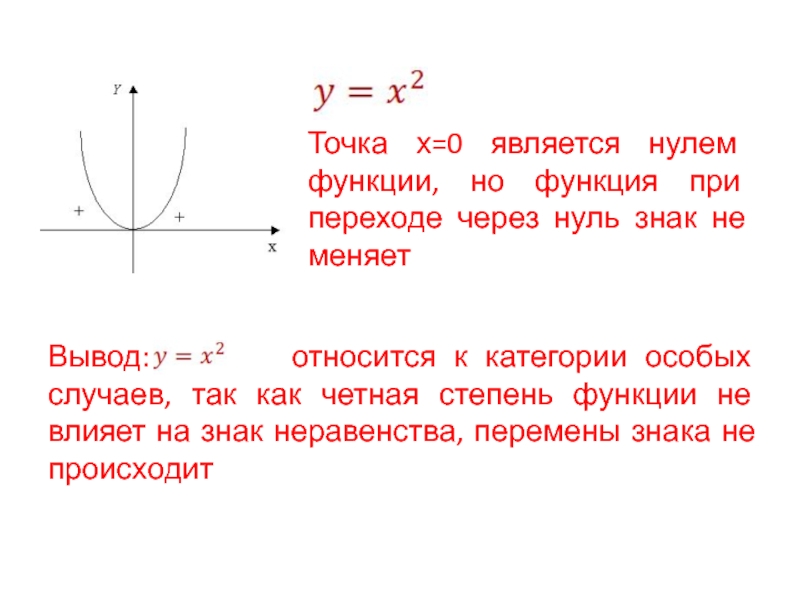
- 4. Точка х=0 является нулем функции, но функция
- 5. УстноРешений нетВывод: выражение, стоящее в четной степени,
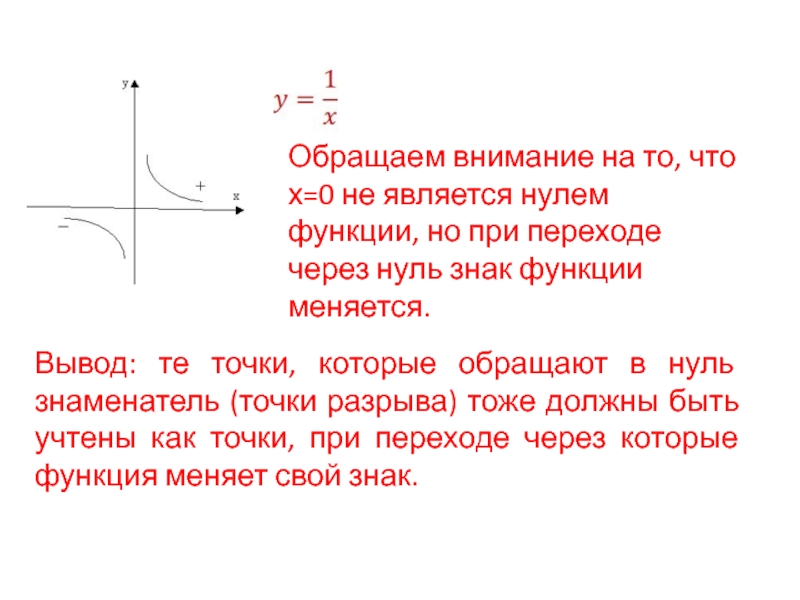
- 6. Обращаем внимание на то, что х=0 не
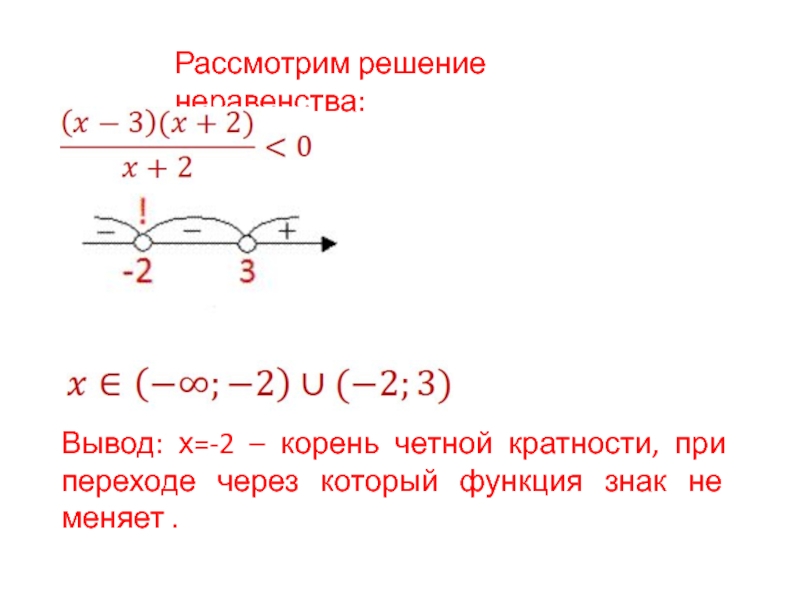
- 7. Рассмотрим решение неравенства:Вывод: х=-2 – корень четной
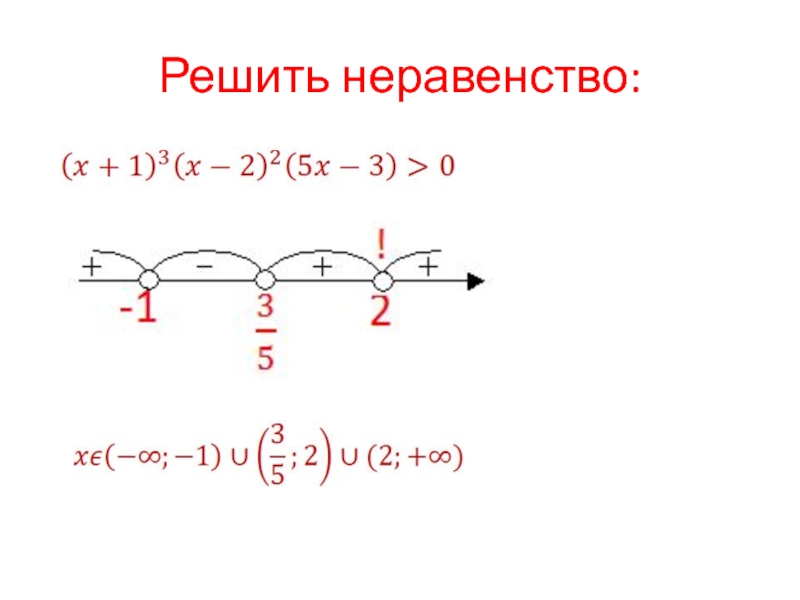
- 8. Решить неравенство:
- 9. Решить неравенство:
- 10. Решить неравенство:
- 11. Слайд 11
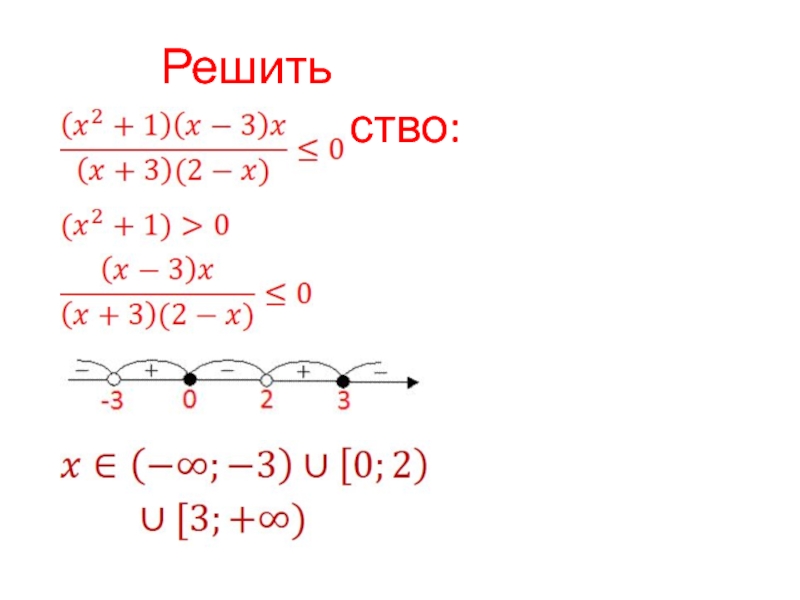
- 12. Решить неравенство:
- 13. Решить неравенства:№ 77(в,г) 78(в,г,е)№ 80
- 14. Скачать презентанцию
Метод интервалов заключается в следующем: Числовая прямая разбивается нулями функции на конечное число интервалов, на каждом из которых функция сохраняет знак.