Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные способы решения квадратных уравнений
Содержание
- 1. Различные способы решения квадратных уравнений
- 2. Определение квадратного уравнения
- 3. Исторические факты о квадратных уравненияхМухаммед Ибн Муса Аль-хорезмиИсаа́к Нью́тонФрансуа Виет
- 4. На протяжении многих веков,ученые разных
- 5. Способы решений квадратных уравнений
- 6. Способ 1: Разложение левой части уравнения на
- 7. Способ 2: Метод выделения полного квадрата
- 8. Способ 3 Решение квадратных уравнений по формуле.
- 9. О корнях квадратного уравнения можно
- 10. Пример:
- 11. Способ 4 Решение уравнений с использованием теоремы Виета
- 12. Теорема, обратная теореме Виета.
- 13. Пример:
- 14. Способ 5 Решение уравнений способом «переброски»ах2 +
- 15. Способ 6: Свойства коэффициентов квадратного уравнения
- 16. Графическое решение квадратного уравнения a2+ bx +
- 17. Пример:х2 - 3х - 4 = 0.х2
- 18. Решение квадратных уравнений с помощью циркуля и
- 19. Итак:1) построим точки
- 20. Слайд 20
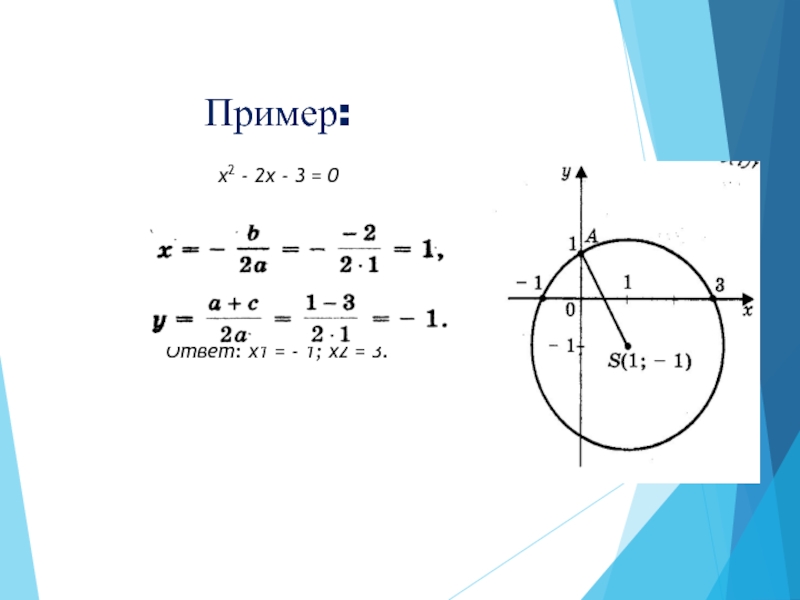
- 21. Пример:х2 - 2х - 3 = 0х1
- 22. Список литературы:1.Алгебра 8 класс. Ю.Н.Макарычев, Н.Г.Миндюк ,
- 23. Скачать презентанцию
Определение квадратного уравнения
Слайды и текст этой презентации
Слайд 3Исторические факты о квадратных уравнениях
Мухаммед Ибн Муса Аль-хорезми
Исаа́к Нью́тон
Франсуа Виет
Слайд 4 На протяжении многих веков,ученые разных стран, в связи
с развитием наук, были вынуждены искать новые способы решения квадратных
уравнений. Очевидно,в наше время известно несколько способов решения этих уравнений.Слайд 6Способ 1:
Разложение левой части уравнения на множители
х2 + 10x –
24 = 0
х2 + 10х – 24 = х2 +
12х - 2х - 24 = х(х + 12) – 2(х + 12) = (х + 12)(х – 2)(х + 12)(х - 2) = 0
х = 2,
х=-12.
Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х – 24 = 0.
Слайд 9
О корнях квадратного уравнения можно судить по знаку
дискриминанта:
D>0 - уравнение имеет 2 различных действительных корня
D=0 - уравнение имеет
2 совпадающих действительных корняD<0 - уравнение имеет 2 мнимых корня
.
Слайд 14Способ 5
Решение уравнений способом «переброски»
ах2 + bх + с =
0, где а ≠ 0.
а2х2 + аbх + ас =
0.у2 + by + ас = 0,
Окончательно получаем
х1 = у1/а и х2 = у2/а.
Слайд 16Графическое решение квадратного уравнения
a2+ bx + c = 0
aх2
= - bx - c.
Построим графики зависимости
у = aх2 и у = - bx - c. Слайд 17Пример:
х2 - 3х - 4 = 0.
х2 = 3х +
4.
Построим графики функций
у = х2
и
у = 3х
+ 4.Ответ: х1 = - 1; х2 = 4.
Слайд 18Решение квадратных уравнений с помощью циркуля и линейки
ах2 + bх
+ с = 0.
OB • OD = OA • OC
OC
= OB • OD/OA= х1 • х2/ 1 = c/a.Слайд 19Итак:
1) построим точки
(центр окружности) и A(0; 1);
2) проведем окружность
с радиусом SA;3) абсциссы точек пересечения этой окружности с осью X являются корнями исходного квадратного уравнения.
Слайд 22Список литературы:
1.Алгебра 8 класс. Ю.Н.Макарычев, Н.Г.Миндюк , К.Г.Нешкова ,И.Е.Феоктистов.
2.Справочник по
элементарной математике. М.Я.Выгодский.
3. https3. https://3. https://ru.wikipedia.org.
4. Алгебра 8 класс А.Г.Мордкович.
5.http://www.webmath.ru/poleznoe/formules_19_5.php