Решение квадратных уравнений над телом кватернионов

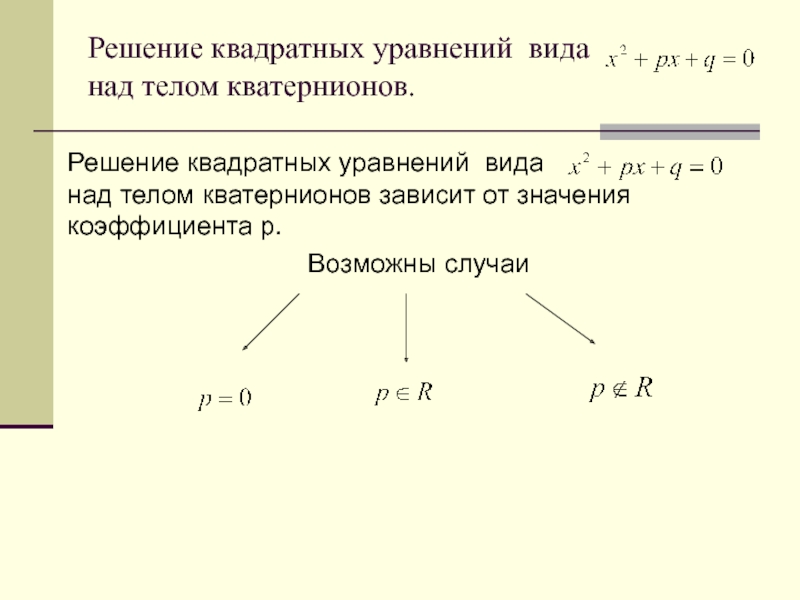
Представление кватерниона q в виде:
где



называется его тригонометрической формой.
Так как и то можно считать мнимой единицей. Причем, у каждого кватерниона своя мнимая единица. В этом заключается существенное отличие тригонометрической формы кватерниона от тригонометрической формы комплексного числа.

тригонометрической форме:
Тогда справедлива формула



Аналогичная формула имеет

место и для возведения в степень комплексного числа.

,где

записан в тригонометрической форме:
И пусть

Тогда справедлива формула




Аналогичная формула имеет место и для извлечения корня n-ой степени из комплексного числа.

, где

и

над телом кватернионов.

Решение квадратных уравнений вида над телом кватернионов зависит от значения коэффициента p.
Возможны случаи

Причем, если

то уравнение может иметь одно, два или бесконечно много решений.
Если то уравнение имеет два различных решения.

и
Введем обозначения:


Тогда возможны две ситуации

коллинеарен

не коллинеарен

Уравнение

будет иметь два различных решения, которые находятся по формуле:

При этом условии
Тогда уравнение имеет два различных

решения, которые находятся по следующей формуле:






Где