Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение простейших тригонометрических уравнений
Содержание
- 1. Решение простейших тригонометрических уравнений
- 2. Под простейшими тригонометрическими уравнениями понимают уравнения вида:,где t – выражение с переменной, a∈.
- 3. Вспомним определение синуса и косинуса угла поворота:sintcost
- 4. xy0101–1–1a >1a
- 5. xy0101t=arcsinat=π–arcsinaa–1–1II случай. Если a∈(–1;1), то уравнение sint=a
- 6. Учитывая периодичность функции синус, каждую из этих
- 7. xy0101–1–1III случай. Если a= –1; 0 или
- 8. xy0101–1–1a >1a
- 9. xy0101t=arccosat=–arccosaa–1–1II случай. Если a∈(–1;1), то уравнение cost=a
- 10. Учитывая периодичность функции косинус, каждую из этих
- 11. xy0101–1–1III случай. Если a= –1; 0 или
- 12. xy101–10линия тангенсовaТак как E(tg)=, то уравнение tgt=a
- 13. xy101–10линия котангенсовaТак как E(ctg)=, то уравнение ctgt=a
- 14. Скачать презентанцию
Под простейшими тригонометрическими уравнениями понимают уравнения вида:,где t – выражение с переменной, a∈.
Слайды и текст этой презентации
Слайд 1Воробьев Леонид Альбертович, г.Минск
Алгебра и начала анализа, 10 класс.
Решение простейших
тригонометрических уравнений.
Слайд 2Под простейшими тригонометрическими уравнениями понимают уравнения вида:
,где t – выражение
с переменной, a∈.
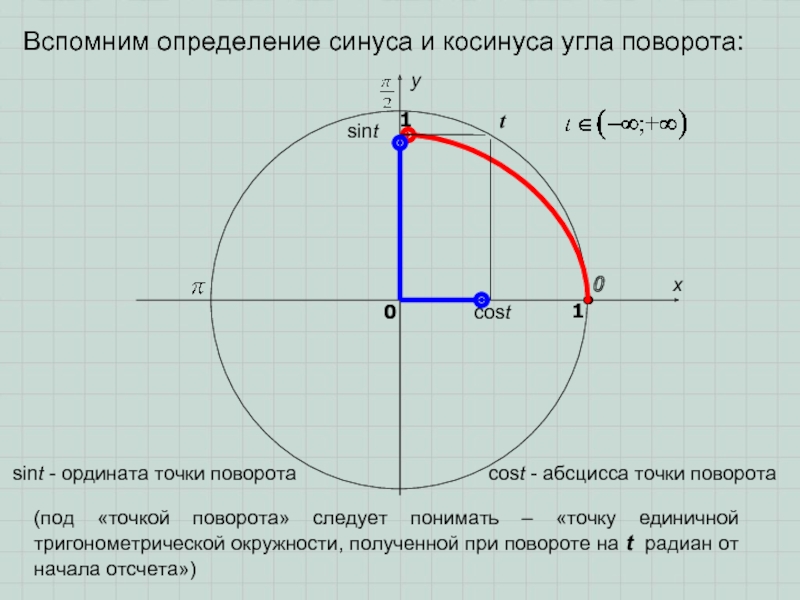
Слайд 3Вспомним определение синуса и косинуса угла поворота:
sint
cost
t
x
y
0
1
0
1
sint - ордината
точки поворота
cost - абсцисса точки поворота
(под «точкой поворота» следует понимать
– «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета»)
Слайд 4
x
y
0
1
0
1
–1
–1
a >1
a
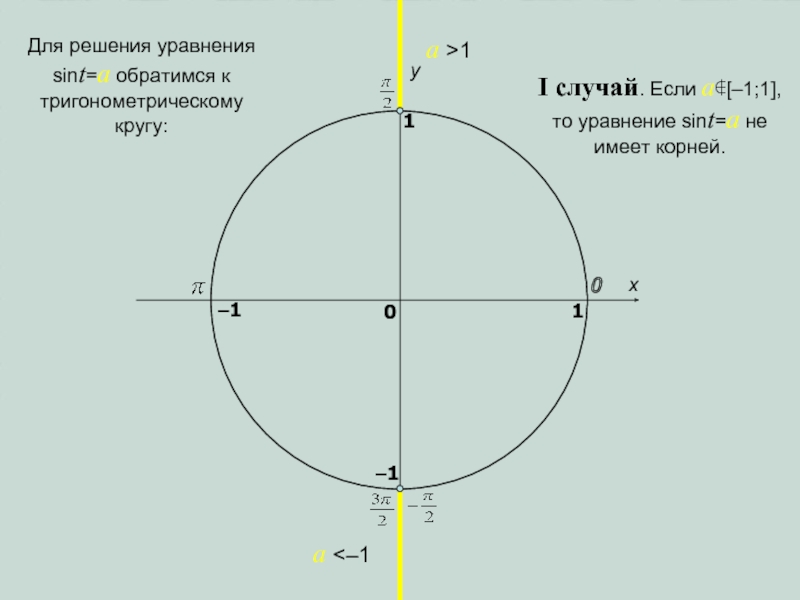
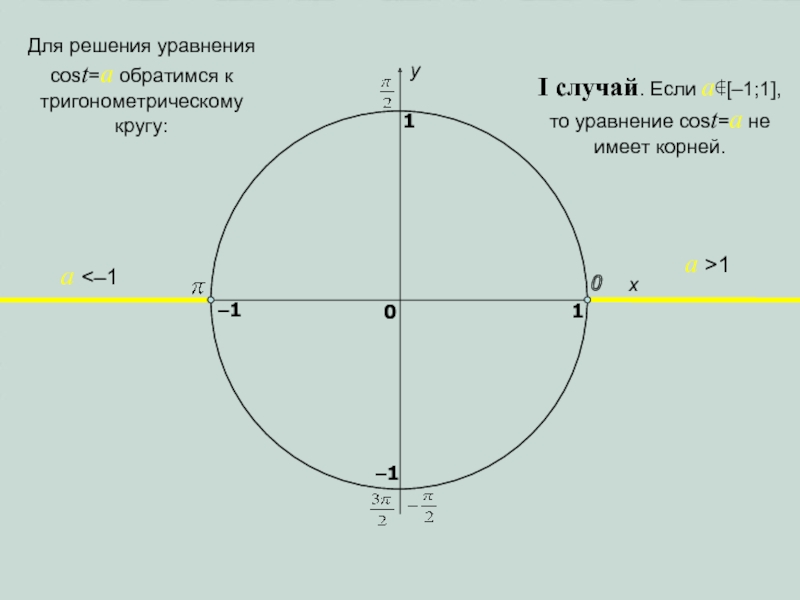
имеет корней.
Для решения уравнения sint=a обратимся к тригонометрическому кругу:
Слайд 5
x
y
0
1
0
1
t=arcsina
t=π–arcsina
a
–1
–1
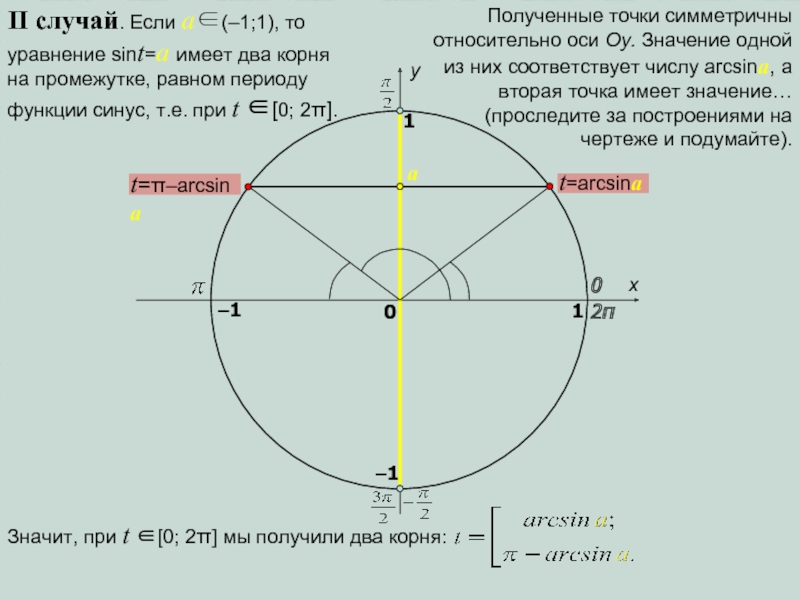
II случай. Если a∈(–1;1), то уравнение sint=a имеет два корня
на промежутке, равном периоду функции синус, т.е. при t ∈[0;
2π].Полученные точки симметричны относительно оси Оу. Значение одной из них соответствует числу arcsina, а вторая точка имеет значение… (проследите за построениями на чертеже и подумайте).
2π
Значит, при t ∈[0; 2π] мы получили два корня:
Слайд 6
Учитывая периодичность функции синус, каждую из этих точек можно получить
при добавлении целого числа полных поворотов, т.е.:
или
Можно заметить, что при
наличии знака «+» перед arcsina к нему прибавляется четное(2k) число π, а при знаке «–» перед arcsina прибавляется нечетное(2m+1) число π. Поэтому эти два равенства можно объединить в одно и записать:Эта формула позволяет найти корни простейшего тригонометрического уравнения sint=a в случаях, если a∈(–1;1).
Слайд 7
x
y
0
1
0
1
–1
–1
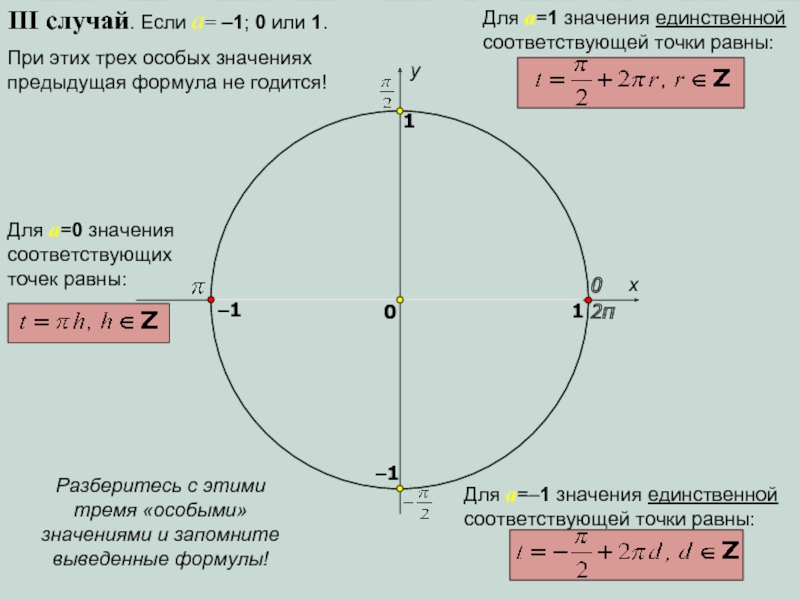
III случай. Если a= –1; 0 или 1.
При этих трех
особых значениях предыдущая формула не годится!
2π
Для a=1 значения единственной соответствующей
точки равны:Для a=0 значения соответствующих точек равны:
Для a=–1 значения единственной соответствующей точки равны:
Разберитесь с этими тремя «особыми» значениями и запомните выведенные формулы!
Слайд 8
x
y
0
1
0
1
–1
–1
a >1
a
имеет корней.
Для решения уравнения cost=a обратимся к тригонометрическому кругу:
Слайд 9
x
y
0
1
0
1
t=arccosa
t=–arccosa
a
–1
–1
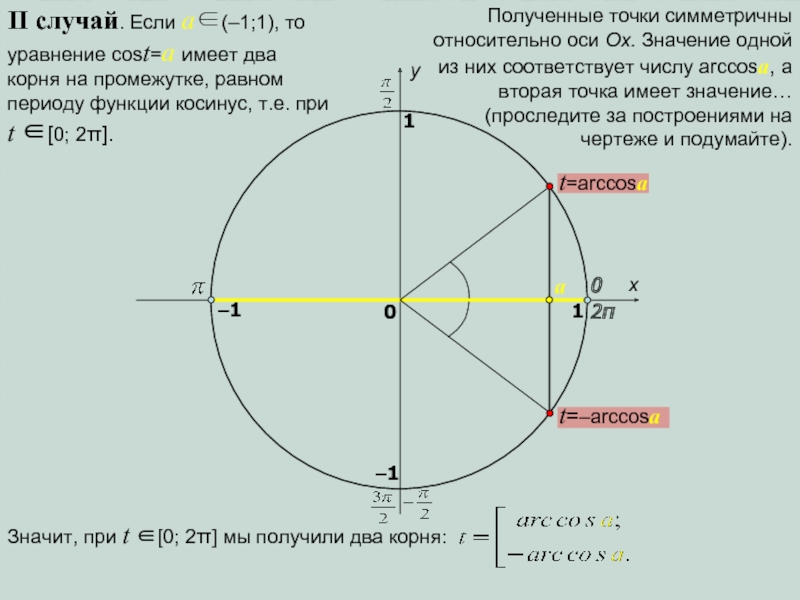
II случай. Если a∈(–1;1), то уравнение cost=a имеет два корня
на промежутке, равном периоду функции косинус, т.е. при t ∈[0;
2π].Полученные точки симметричны относительно оси Оx. Значение одной из них соответствует числу arccosa, а вторая точка имеет значение… (проследите за построениями на чертеже и подумайте).
2π
Значит, при t ∈[0; 2π] мы получили два корня:
Слайд 10
Учитывая периодичность функции косинус, каждую из этих точек можно получить
при добавлении целого числа полных поворотов, т.е.:
Эти записи отличаются друг
от друга только знаками перед arccosa. Поэтому эти два равенства можно объединить в одно и записать:Эта формула позволяет найти корни простейшего тригонометрического уравнения cost=a в случаях, если a∈(–1;1).
Слайд 11
x
y
0
1
0
1
–1
–1
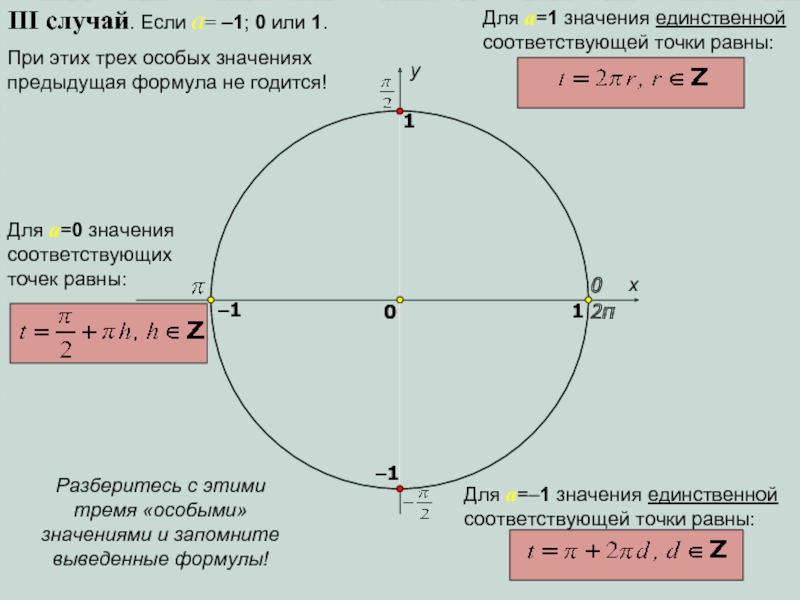
III случай. Если a= –1; 0 или 1.
При этих трех
особых значениях предыдущая формула не годится!
2π
Для a=1 значения единственной соответствующей
точки равны:Для a=0 значения соответствующих точек равны:
Для a=–1 значения единственной соответствующей точки равны:
Разберитесь с этими тремя «особыми» значениями и запомните выведенные формулы!
Слайд 12x
y
1
0
1
–1
0
линия тангенсов
a
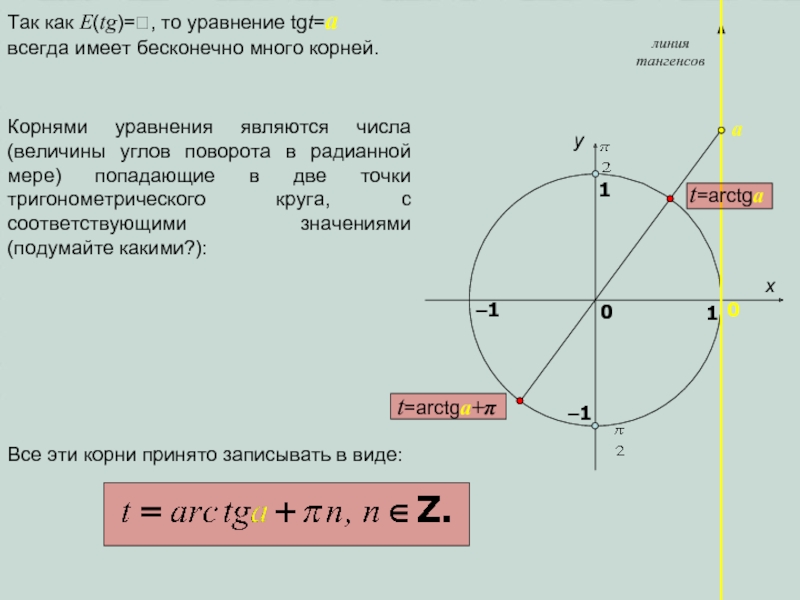
Так как E(tg)=, то уравнение tgt=a всегда имеет бесконечно
много корней.
–1
Корнями уравнения являются числа (величины углов поворота в радианной
мере) попадающие в две точки тригонометрического круга, с соответствующими значениями (подумайте какими?):Все эти корни принято записывать в виде:
Слайд 13x
y
1
0
1
–1
0
линия котангенсов
a
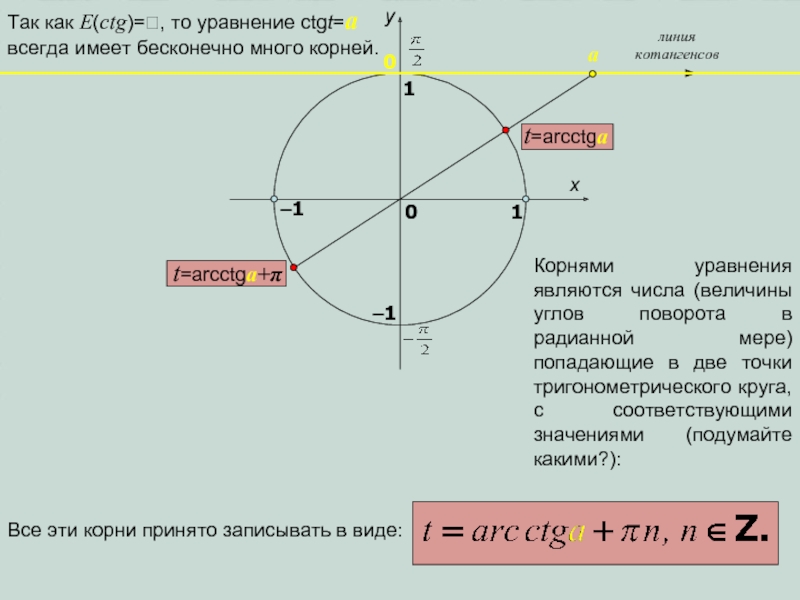
Так как E(ctg)=, то уравнение ctgt=a всегда имеет бесконечно
много корней.
–1
Корнями уравнения являются числа (величины углов поворота в радианной
мере) попадающие в две точки тригонометрического круга, с соответствующими значениями (подумайте какими?):Все эти корни принято записывать в виде:
Теги
