Уравнение касательной

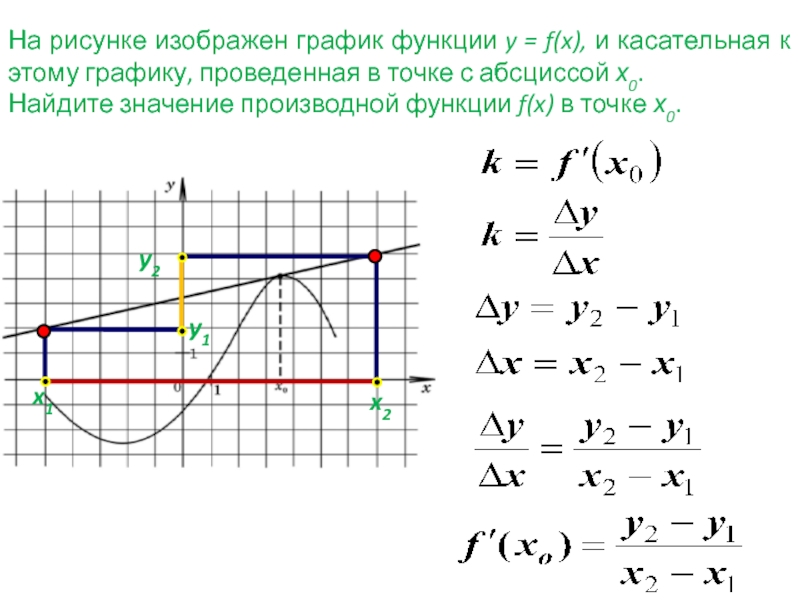
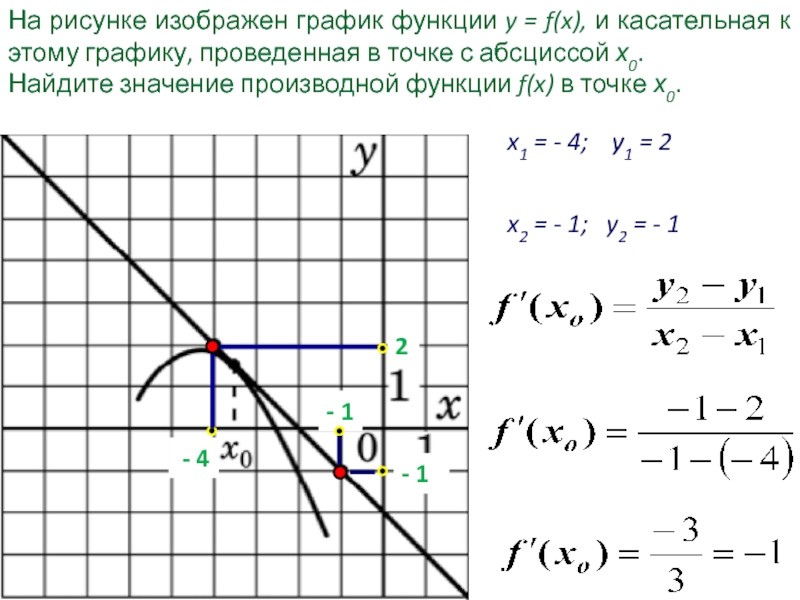
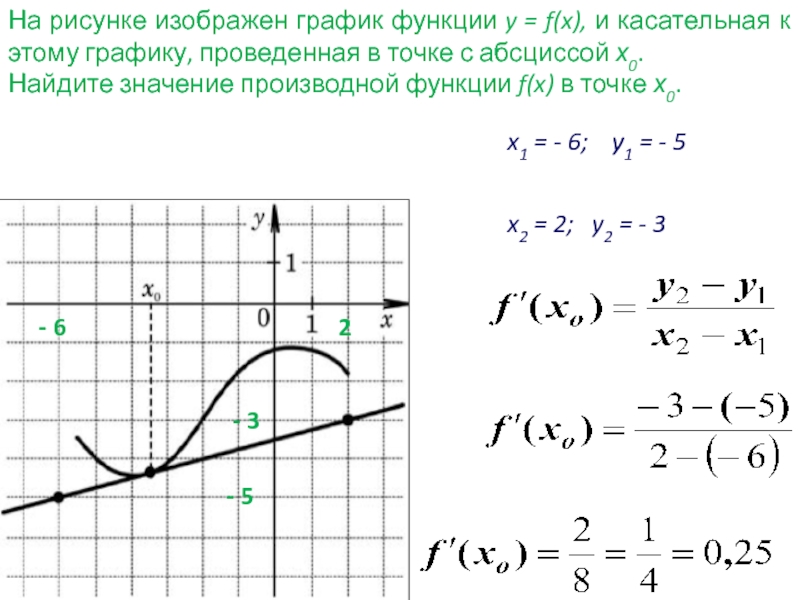
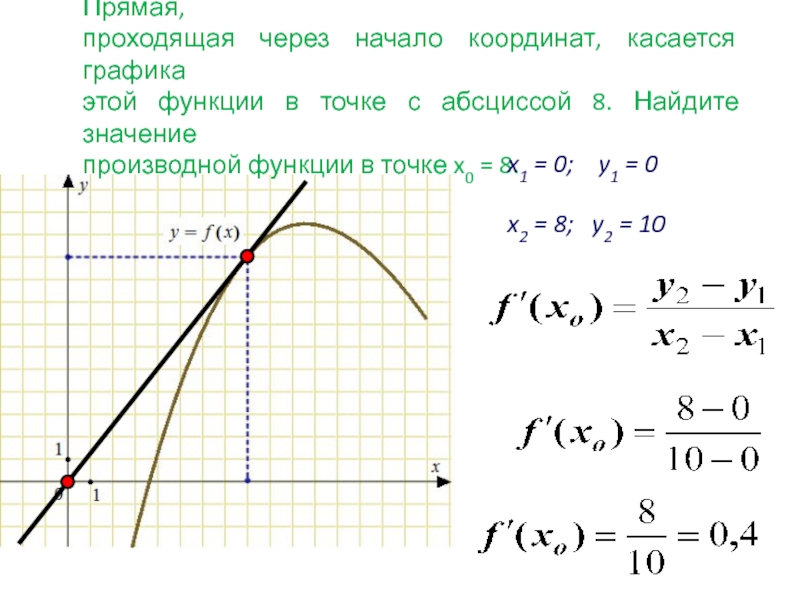
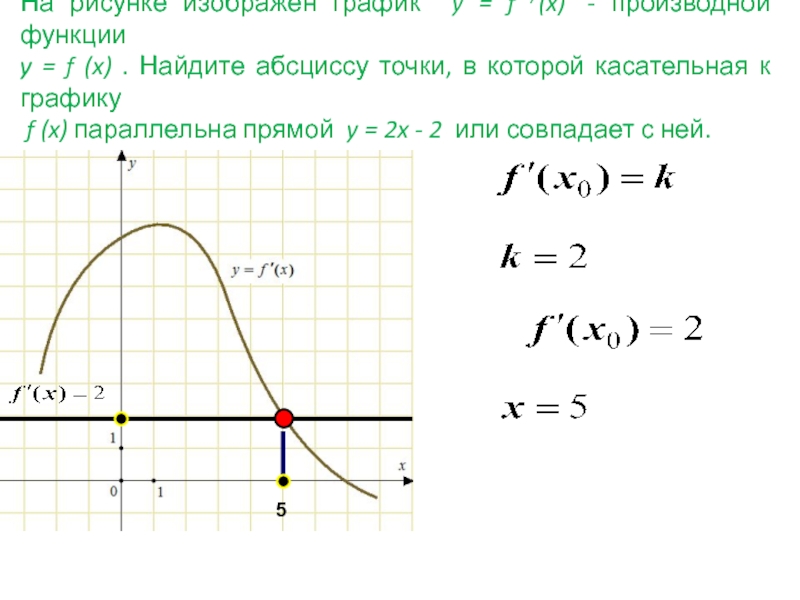
абсциссой х0 называется прямая, проходящая через точку (x0 ; f(x0))

Алгоритм уравнения касательной

Обозначить абсциссу точки касания х0
Вычислить f(х0)
Найти f |(x)
Найти f |(х0)
Подставить найденные числа в формулу (1)

(1)

Уравнение касательной

Угловой коэффициент касательной

точке с абсциссой x0.
а) f(x) = x2 + x

б) f(x) = sin x, x0 = π/2
f(π/2) = 1
f /(x) = cos x
f /(π/2) = 0
y = 1 + 0(x – π/2)
y = 1

данной прямой

б) f(x) = 1/3x3 – x2 – x

к этому графику, проведенная в точке с абсциссой х0.
Найдите

x2

x1

y2

y1

= 2
x2 = - 1; y2 = - 1
На

к этому графику, проведенная в точке с абсциссой х0.
Найдите

x1 = - 6; y1 = - 5

x2 = 2; y2 = - 3

- 6

- 5

2

- 3

проходящая через начало координат, касается графика
этой функции в точке

x1 = 0; y1 = 0

x2 = 8; y2 = 10

функции
y = f (x) . Найдите абсциссу точки, в

5

графику функции y = x3

y = f(x0) + f / (x0)(x – x0)
f / (x0) = – 4
f / (x) = 3x2 + 14x + 7
3x02 + 14x0 + 7 = - 4
3x02 + 14x0 + 11 = 0
x0 = – 1 или x0 = – 11/3
f(– 1) = – 1 + 7 – 7 – 6 = – 7
y = – 7 – 4(x + 1)
y = – 4x – 11