Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение уравнений и неравенств с параметрами
Содержание
- 1. Решение уравнений и неравенств с параметрами
- 2. более глубоко изучить особенности решения уравнений и
- 3. - дать понятие «уравнение с параметрами»;- рассмотреть
- 4. Если в уравнении некоторые коэффициенты заданы не
- 5. 1) найти множество всех доступных значений параметров;2)
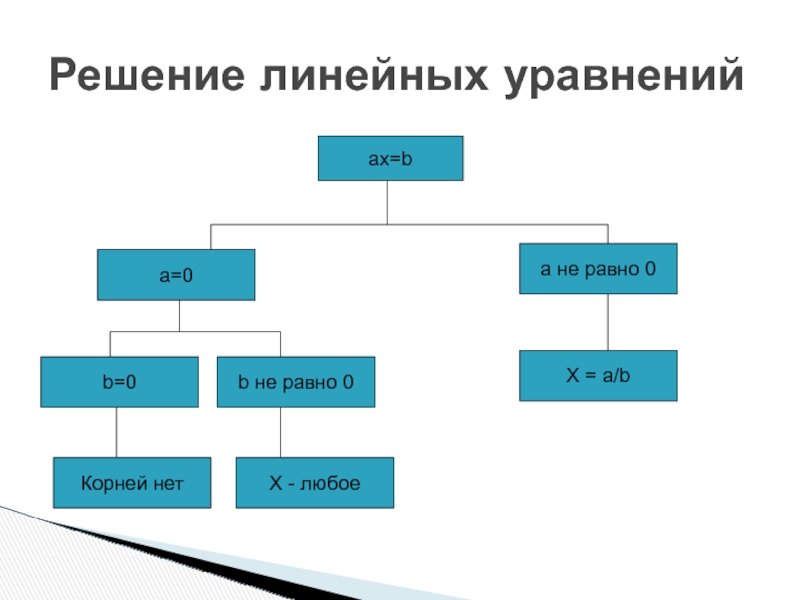
- 6. Решение линейных уравнений ах=bа=0а не равно 0b=0b не равно 0Корней нетХ - любоеХ = a/b
- 7. Зависимость количества решений системы линейных уравнений от
- 8. Решение:x/a+x=2x(1/a+1)=2x(1+a)/a=2При a=0 уравнение не имеет смыслаПри a+1=0,
- 9. Ход решенияПостроение графика функции Анализ графика функцииПри каких значениях параметра а уравнение имеет ровно 3 корня.
- 10. Построение графика функции Построим график функции
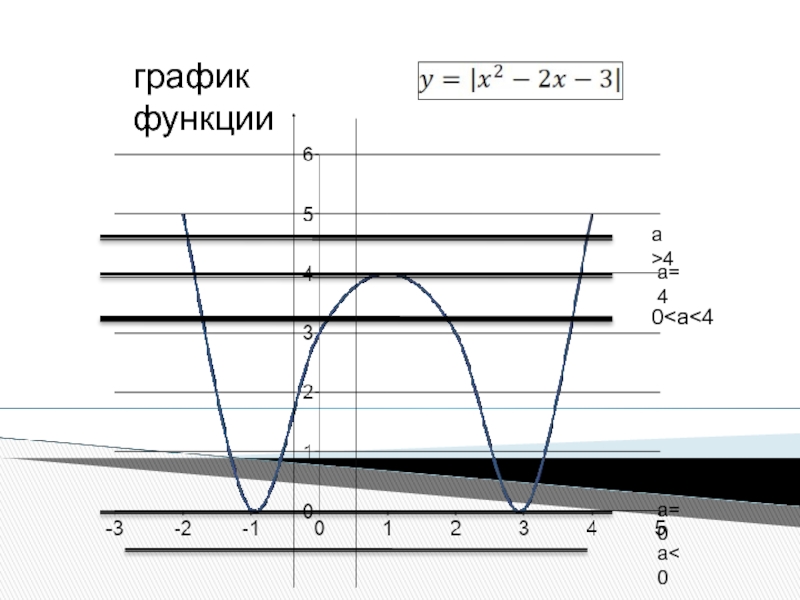
- 11. график функции
- 12. график функции 0
- 13. АНАЛИЗ ГРАФИКА ФУНКЦИИПри a4 - два решенияПри 0
- 14. Решение неравенства ах>bЕсли a>bТоX>b/aЕсли a=aНеравенство решений не имеетЕсли b
- 15. Находим область определения данного неравенства.Сводим неравенство к
- 16. Решить относительно x неравенство :mx-2x > 2(x-1)
- 17. Далингер В. А. “Геометрия помогает алгебре”.
- 18. Скачать презентанцию
более глубоко изучить особенности решения уравнений и неравенств с параметрами, выявить наиболее рациональные методики решения, быстро приводящего к ответу Цель работы
Слайды и текст этой презентации
Слайд 2более глубоко изучить особенности решения уравнений и неравенств с параметрами,
выявить наиболее рациональные методики решения, быстро приводящего к ответу
работы
Слайд 3- дать понятие «уравнение с параметрами»;
- рассмотреть наиболее часто встречающиеся
типы уравнений, неравенств и их систем;
- предложить основные способы решения
задач с параметрами.Задачи работы
Слайд 4Если в уравнении некоторые коэффициенты заданы не конкретными числовыми значениями,
а обозначены буквами, то они называются параметрами, а уравнение параметрическим.
. Понятие уравнения с параметрами
Слайд 51) найти множество всех доступных значений параметров;
2) перенести все члены,
содержащие неизвестное, в левую часть уравнения, а все члены, не
содержащие неизвестного в правую;3) привести подобные слагаемые;
4) решать уравнение ax = b.
Методика решения уравнений
Слайд 7Зависимость количества решений системы линейных уравнений от коэффициентов системы
Если
а1/а2 не равно
b1/b2, то решение –
Единственное
Если
а1/а2 = b1/b2,
Но не равно с1/с2,
то решений нет
Если
а1/а2 = b1/b2 = с1/с2,
то решений
Бесконечное
Множество
Слайд 8Решение:
x/a+x=2
x(1/a+1)=2
x(1+a)/a=2
При a=0 уравнение не имеет смысла
При a+1=0, a=-1 уравнение принимает
вид 0x=2, не имеет решения
При a≠0, a≠-1 уравнение имеет единственный
корень x=2a/(a+1)Ответ: при a=0 уравнение не имеет смысла, при а=-1 решений нет, при а≠0, а≠-1 х=2а/(а+1)
Решить уравнение: x/a+3=5-x
Слайд 9Ход решения
Построение графика функции
Анализ графика функции
При каких значениях параметра
а уравнение
имеет ровно 3 корня.
Слайд 10Построение графика функции
Построим график функции
, и при значениях y<0 отразим симметрично оси ox.
2.Координаты вершины (1;4)
3.Точки пересечения с осью ох:y=0
((-1;0)и(3:0))
1.Общая характеристика функции
4.Дополнительные точки
Слайд 13АНАЛИЗ ГРАФИКА ФУНКЦИИ
При a
при а >4 - два решения
При 0
а=4 три решения (x=1+2 , x=1-2 , x = 1 )
Ответ: при а=4 –три решения
Слайд 15Находим область определения данного неравенства.
Сводим неравенство к уравнению.
Выражаем а как
функцию от х.
В системе координат хОа строим графики функций а
=ƒ (х) для тех значений х, которые входят в область определения данного неравенства.Находим множества точек, удовлетворяющих данному неравенству.
Исследуем влияние параметра на результат.
найдём абсциссы точек пересечения графиков.
зададим прямую а=соnst и будем сдвигать её от -∞ до+∞
Записываем ответ.
Решения неравенств с параметрами:
Слайд 16Решить относительно x неравенство :
mx-2x > 2(x-1)
Решение:
x-2x>-2-1
(m-2)x>-3
Данное неравенство является
линейным, поэтому контрольным значением для него будет m-2=0
Далее имеем:
При m-2>0.
то есть m>2, x>-3/(m-2), x>3/(2-m)При m-2<0, то есть m<2, x<3/(2-m)
При m=2 неравенство принимает вид 0x>-3. Здесь
x-любое действительное число.
Ответ: при m>2 x>3/(2-m); при m<2 x<3/(2-m);
при m=2 x-любое действительное число
Слайд 17 Далингер В. А. “Геометрия помогает алгебре”. Издательство “Школа -
Пресс”. Москва 1996 г.
Далингер В. А. “Все для обеспечения успеха
на выпускных и вступительных экзаменах по математике”. Издательство Омского педуниверситета. Омск 1995 г.Окунев А. А. “Графическое решение уравнений с параметрами”. Издательство “Школа - Пресс”. Москва 1986 г.
Письменский Д. Т. “Математика для старшеклассников”. Издательство “Айрис”. Москва 1996 г.
Ястрибинецкий Г. А. “Уравнений и неравенства, содержащие параметры”. Издательство “Просвещение”. Москва 1972 г.
Г. Корн и Т.Корн “Справочник по математике”. Издательство “Наука” физико–математическая литература. Москва 1977 г.
Амелькин В. В. и Рабцевич В. Л. “Задачи с параметрами” .
www.bymath.net/studyguide/alg/sec/alg31.html
www.math4you.ru/theory/TerVerMatStat/TerVerKom/
www.pm298.ru›
Литература
