Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач по теореме Пифагора
Содержание
- 1. Решение задач по теореме Пифагора
- 2. Ее знали в Китае, Вавилонии, Египте. ( за 1200 лет) до Пифагора
- 3. Историческая справкаЕсли дан нам треугольник И притом
- 4. Теорема Пифагора имеет богатую историю. Оказывается, она
- 5. Во Франции и некоторых областях Германии в
- 6. Формулировка теоремыАСВВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 7. Доказательство теоремы1. Достроим АВС до квадрата СКРД
- 8. . В некоторых странах в средние века,
- 9. Теорема Пифагора ( другая формулировка)Сумма площадей квадратов,
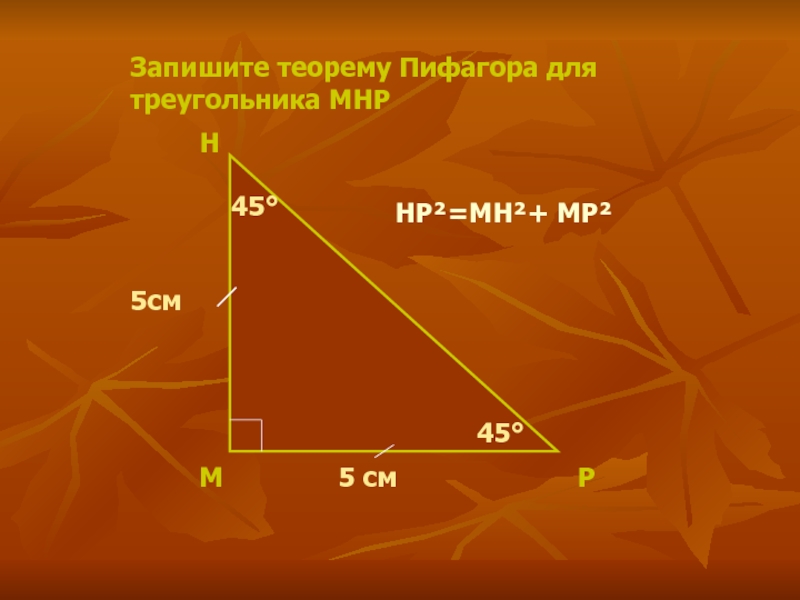
- 10. Запишите теорему Пифагора для треугольника МНРМНР5 см5см4545HP²=MH²+ MP²
- 11. Найдите неизвестные элементы в треугольнике:А12 см60AB²=AC²+ BC²AC²=AB²- BC², AC²= 12²-6²=144-36= =108 AC =63
- 12. Найдите недостающие стороны прямоугольного треугольника, если а и в его катеты, а с -гипотенуза32441522
- 13. Веревочный треугольник3, 4, 5
- 14. задача индийского математика XII в. Бхаскары«На берегу
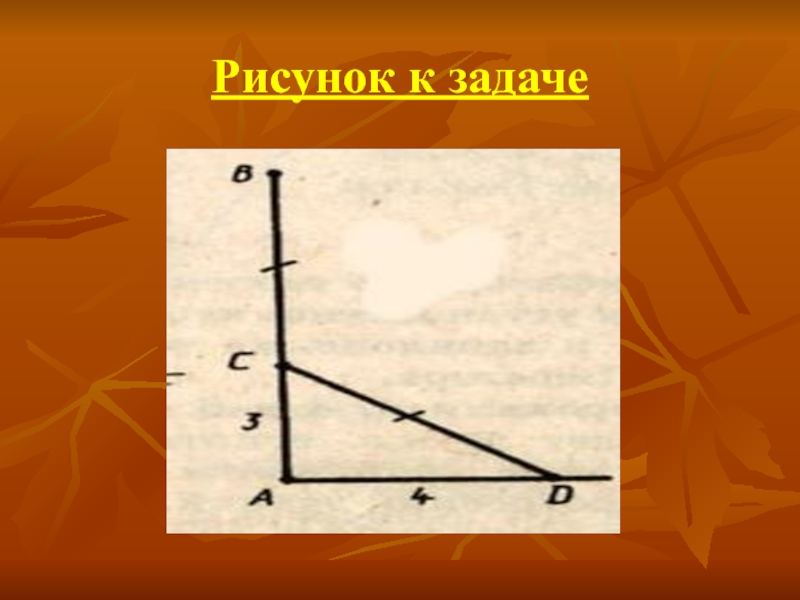
- 15. Рисунок к задаче
- 16. Задача 1:«На глубине 12 футов растет лотос
- 17. Задача 2. Случися некоему человеку к стене
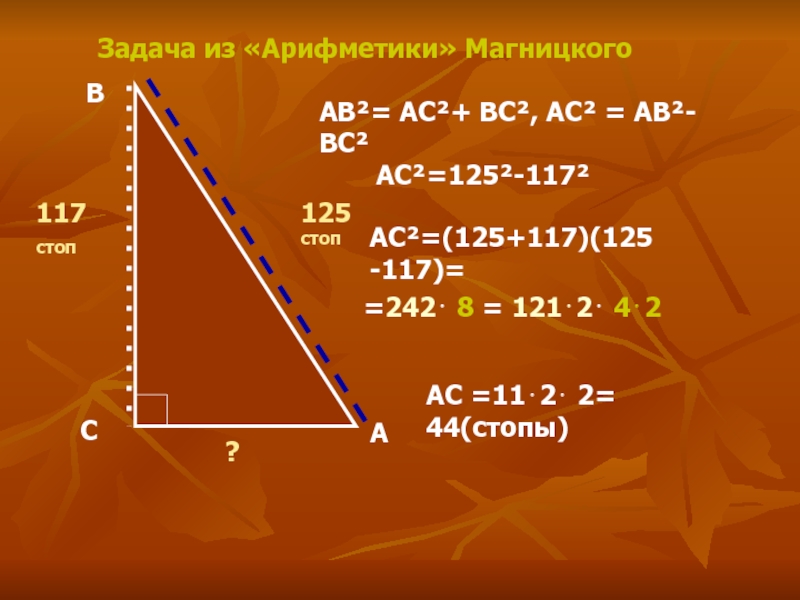
- 18. Задача из «Арифметики» МагницкогоАВСАВ²= АС²+ ВС², АС²
- 19. заключение
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Историческая справка
Если дан нам треугольник
И притом с прямым углом,
То
квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим
–И таким простым путем
К результату мы придем.
Это одна из самых известных теорем древности, называемая теоремой Пифагора. Ее и сейчас знают практически все, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания «о пифагоровых штанах». Причина такой популярности теоремы Пифагора триедина: это простота – красота – значимость
Слайд 4
Теорема Пифагора имеет богатую историю. Оказывается, она задолго до Пифагора
была известна египтянам, вавилонянам, китайцам и индийцам. За восемь веков
до нашей эры эта теорема была хорошо известна индийцам под названием «правила веревки» и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель – моралист Плутарх, математик V века Прокл и другие.Слайд 5Во Франции и некоторых областях Германии в средневековье теорему Пифагора
почему-то называли «мостом ослов». У математиков арабского Востока эта теорема
получила название «теоремы невесты». Дело в том, что в некоторых списках «Начал» Евклида эта теорема называлась «теоремой нимфы» за сходство чертежа с пчелкой, бабочкой, что по-гречески называлось нимфой. Но словом эти греки называли еще некоторых богинь, а также вообще молодых женщин, и невест. При переводе с греческого арабский переводчик, не обратив внимание на чертеж, перевел слова «нимфа» как «невеста», а не «бабочка». Так появилось ласковое название знаменитой теоремы – «теорема невесты».Слайд 6Формулировка теоремы
А
С
В
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 7Доказательство теоремы
1. Достроим
АВС до квадрата СКРД со стороной
( а + в );
SСКРД= ( а + в)2 =
а2 + 2ав + в22.
ВСА =
АКЕ =
ЕРМ =
МДВ ( по двум катетам )
С
А
В
Д
М
Р
Е
К
SВСА = SАКЕ = SЕРМ= SМДВ = ав/2
3. ВАЕМ – квадрат, SВАЕМ = c2
4. SСКРД= SВАЕМ+ SВСА+ SАКЕ+ SЕРМ+ SМДВ
5. ( а + в)2 = с2 + 4 * ав/2
а2 + 2ав + в2 = с2 + 2ав, откуда
с2 = а2 + в2
Дано:
АВС, Доказать: с2 = а2 + в2 Доказательство:
Слайд 8. В некоторых странах в средние века, чтобы получить ученое
звание магистра, нужно было изобрести свое собственное доказательство этой теоремы,
поэтому существует так много ее доказательств. В книге английского педагога Е.Лумиса, например, обсуждаются и классифицируется 370 доказательств теоремы Пифагора. С глубокой древности математики находят все новые и новые доказательства теоремы, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства не сохранилось никаких следов.Слайд 9Теорема Пифагора ( другая формулировка)
Сумма площадей квадратов, построенных на катетах
прямоугольного треугольника, равна площади квадрата, построенного на его гипотенузе
Именно
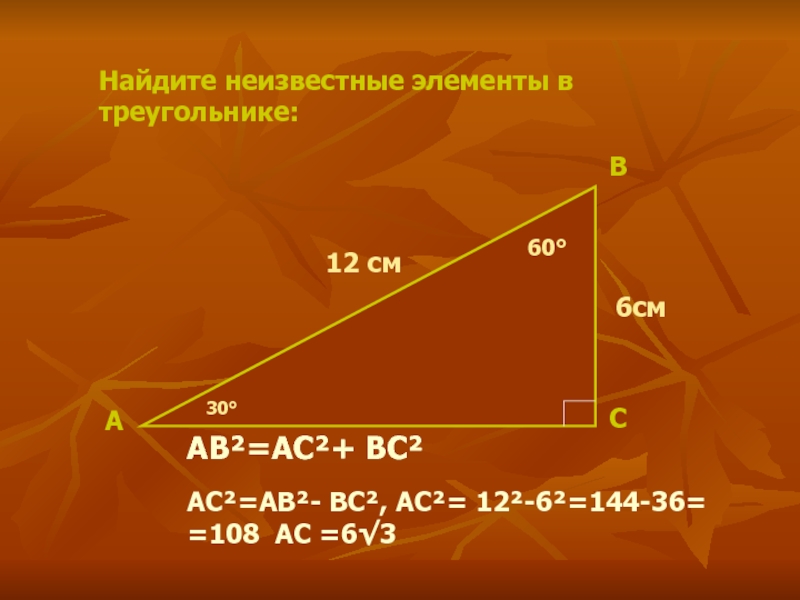
так выглядела классическая формулировка теоремы. Картинка, иллюстрирующая теорему Пифагора, была ранее своеобразным символом геометрии, а в среде российских гимназистов получила название « Пифагоровы штаны».Саму теорему они переиначили так: «Пифагоровы штаны на все стороны равны». И в этой шуточной формулировке запоминали ее на всю жизнь.Слайд 11Найдите неизвестные элементы в треугольнике:
А
12 см
60
AB²=AC²+ BC²
AC²=AB²- BC², AC²= 12²-6²=144-36=
=108 AC =63
Слайд 12Найдите недостающие стороны прямоугольного треугольника, если а и в его
катеты, а с -гипотенуза
3
244
15
22
Слайд 14задача индийского математика XII в. Бхаскары
«На берегу реки рос тополь
одинокий
Вдруг ветра порыв его ствол
надломал.Бедный тополь упал.
И угол прямой с теченьем реки его
ствол составлял.
Запомни теперь, что в том месте
река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от
ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
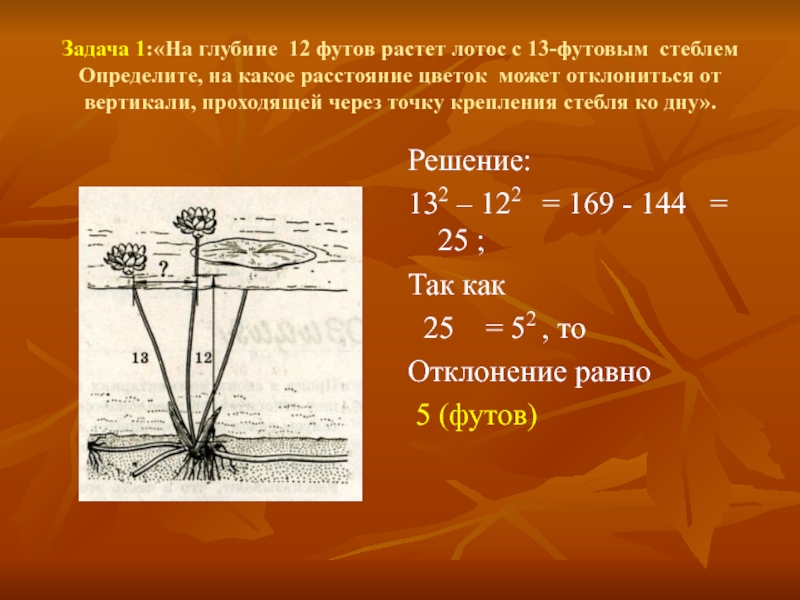
Слайд 16Задача 1:«На глубине 12 футов растет лотос с 13-футовым стеблем
Определите, на какое расстояние цветок может отклониться от вертикали,
проходящей через точку крепления стебля ко дну».Решение:
132 – 122 = 169 - 144 = 25 ;
Так как
25 = 52 , то
Отклонение равно
5 (футов)