Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия в пространстве. Симметрия в природе и на практике.
Содержание
- 1. Симметрия в пространстве. Симметрия в природе и на практике.
- 2. 1. Раздел геометрии, в котором изучаются фигуры в пространстве?
- 3. 2.Преобразование пространства, сохраняющее расстояние между соответвующими точками?
- 4. 3.Фигура, образованная простой замкнутой ломаной и ограниченной ею частью плоскости, называется...
- 5. 4. “Геометрическое тело”, поверхность которого состоит из многоугольников, называется...
- 6. 5. Через две пересекающиеся прямые проходит…плоскость.
- 7. 6. Утверждения, которые необходимо доказать, называются...
- 8. 7. Как называются два двугранных угла, если они имеют одну и ту же величину?
- 9. 8.Плоскости, которые... хотя бы одну общую точку, называются пересекающимися.
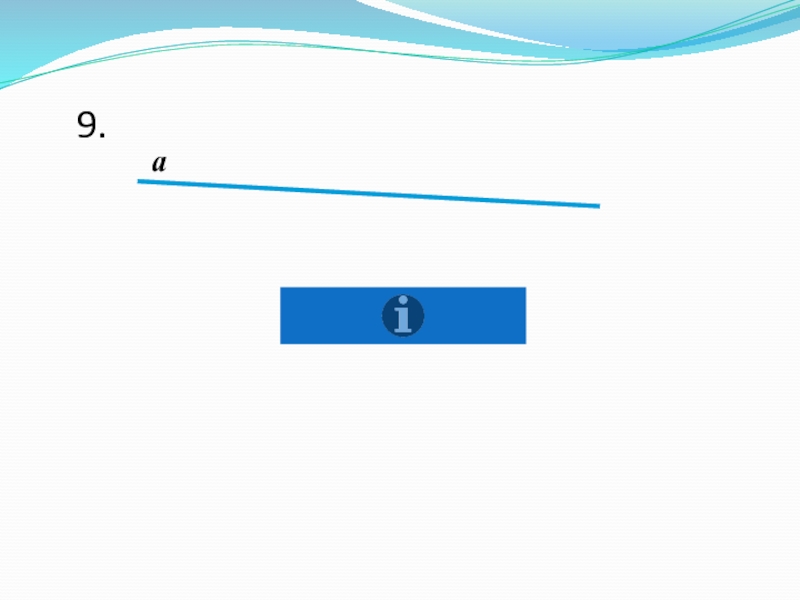
- 10. a9.
- 11. 1. Стереометрия2. Изометрия3.
- 12. Симметрия в пространстве. Симметрия в природе и на практике
- 13. «Симметрия» (нем. Symmetrie, франц. symetrie, греч. symmetria
- 14. «Раз, стоя перед черной доской и рисуя
- 15. СодержаниеОсновные определенияСимметрия на плоскостиСимметрия в пространствеСимметрия в природеСимметрия на практике
- 16. Две точки называются симметричными относительно данной точки
- 17. Центральная симметрияЦентральная симметрия -
- 18. Примеры центральной симметрии
- 19. Центральный зал станции
- 20. Кактус
- 21. Шахматная доска
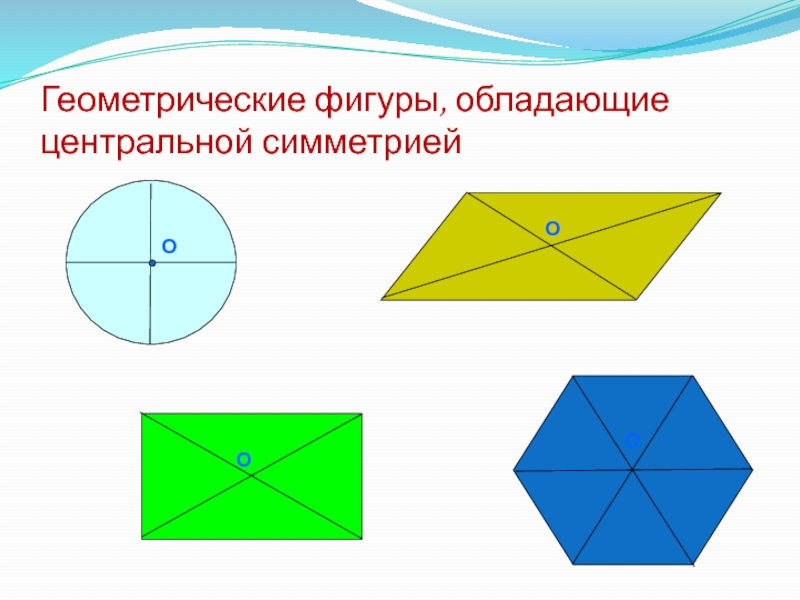
- 22. Геометрические фигуры, обладающие центральной симметриейОООО
- 23. Осевая симметрия Две точки называются симметричными относительно
- 24. Осевой симметрией с осью l называется отображение
- 25. Фигура называется симметричной относительно прямой l, если
- 26. Осевая симметрия вокруг нас Фигуры, обладающие осевой симметрией
- 27. Слайд 27
- 28. Геометрические фигуры, обладающие осевой симметрией
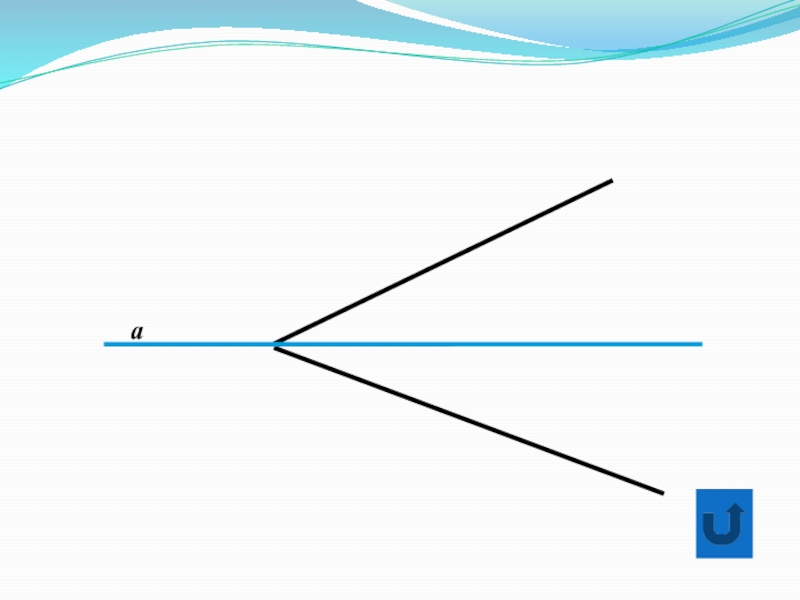
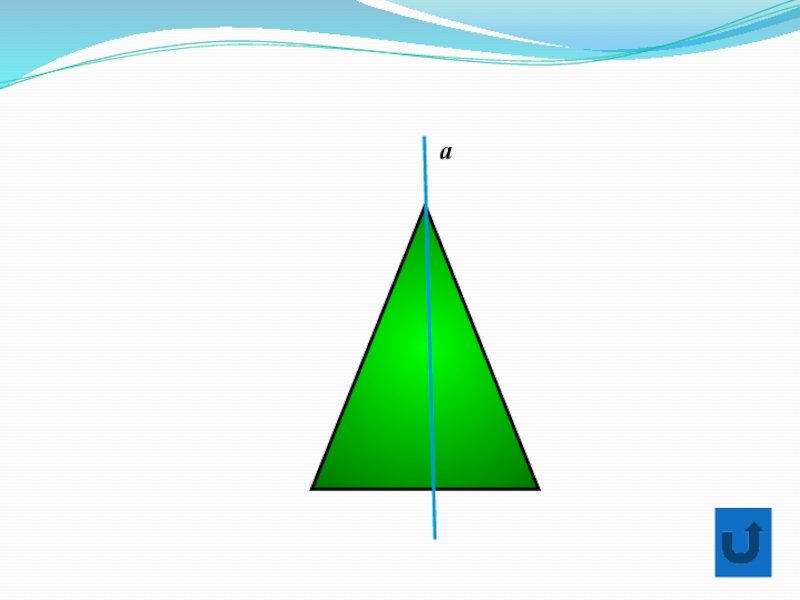
- 29. a
- 30. a
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Симметрия в пространстве. Зеркальная симметрия.При зеркальной симметрии
- 37. Точки А и А1 называются симметричными относительно
- 38. Симметрией относительно плоскости называется преобразование пространства, при
- 39. Зеркальная симметрия является геометрическим преобразованием.При зеркальной симметрии
- 40. Мир зеркальной симметрии.Симметрия в природе и на практике.
- 41. Отражение в воде – хороший
- 42. Примерами зеркальных отражений одна другой могут служить рука человека.
- 43. Симметрия – это идея, с помощью которой
- 44. Слайд 44
- 45. Слайд 45
- 46. Мечеть Кул Шариф
- 47. Узоры на коврах
- 48. Симметрия в быту
- 49. Орнаменты
- 50. Слайд 50
- 51. Бабочки
- 52. Слайд 52
- 53. Человек
- 54. Тигр
- 55. Являются ли точки симметричными относительно данной точкиМ
- 56. Какие из следующих букв имеют центр симметрии:
- 57. Какие из следующих букв имеют ось симметрии:
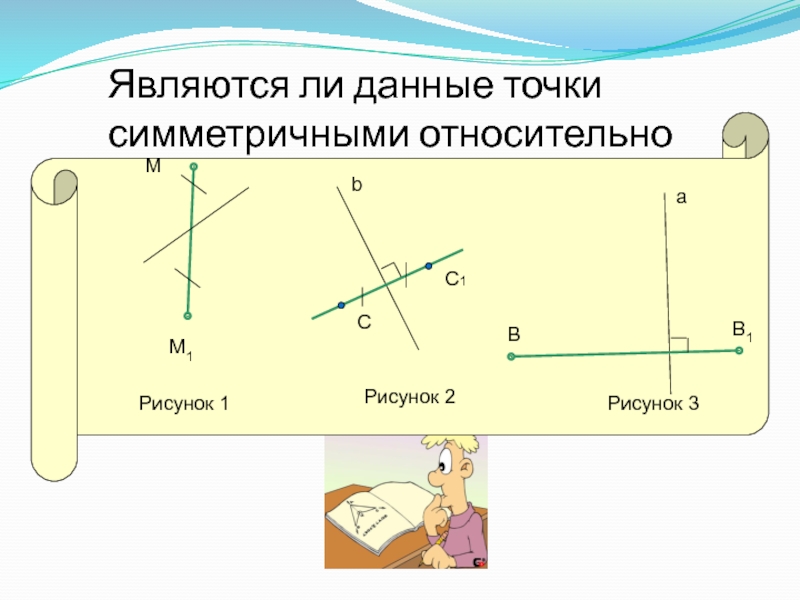
- 58. Являются ли данные точки симметричными относительно оси ?М М1 Рисунок 1Рисунок 2bС1СаBВ1Рисунок 3
- 59. 3ЯО=И,
- 60. Слайд 60
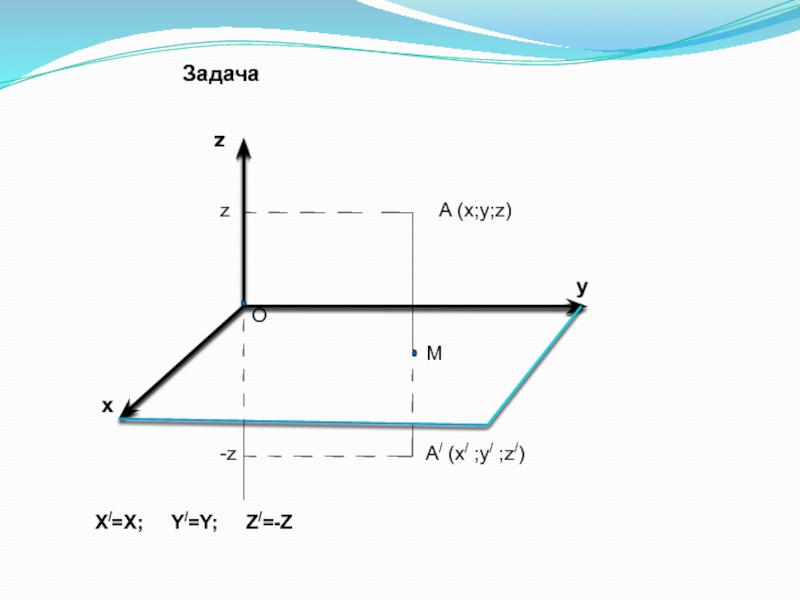
- 61. zz-zА (х;у;z)уМО А/ (х/ ;у/ ;z/)xЗадача X/=X; Y/=Y; Z/=-Z
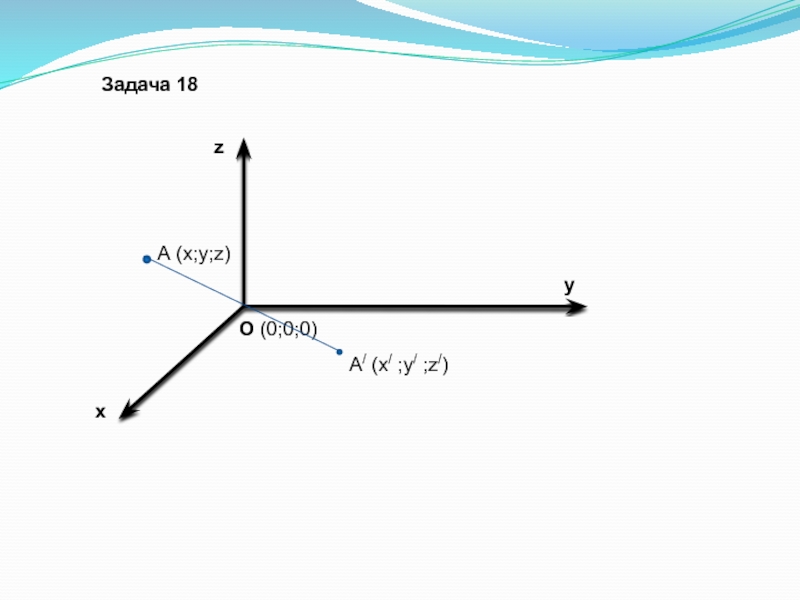
- 62. zО (0;0;0)уxА (х;у;z)А/ (х/ ;у/ ;z/)Задача 18
- 63. Урок окончен. Спасибо за внимание.
- 64. Скачать презентанцию
1. Раздел геометрии, в котором изучаются фигуры в пространстве?
Слайды и текст этой презентации
Слайд 43.Фигура, образованная простой замкнутой ломаной и ограниченной ею частью плоскости,
называется...
Слайд 111. Стереометрия
2. Изометрия
3. Многоугольник
4.
Многогранник
5. Единственная
6. Теорема
7.
Равными8. Имеют
9. Прямая
Слайд 13«Симметрия» (нем. Symmetrie, франц. symetrie, греч. symmetria ) – соразмерность,
пропорциональность в расположении частей чего-нибудь по обе стороны от середины,
центра.(Толковый словарь иностранных слов Л.П. Крысина.)
Слайд 14
«Раз, стоя перед черной доской и рисуя на ней мелом
разные фигуры, я вдруг был поражен мыслью: почему симметрия была
приятна для глаз? Что такое симметрия? Это врожденное чувство. На чем же оно основано?… Разве во всем в жизни симметрия?»(Отрывок из книги «Отрочество» Льва Толстого)
Слайд 15Содержание
Основные определения
Симметрия на плоскости
Симметрия в пространстве
Симметрия в природе
Симметрия на практике
Слайд 16Две точки называются симметричными относительно данной точки (центра симметрии) или
центрально симметричными, если данная точка является серединой соединяющего их отрезка.
Слайд 17
Центральная симметрия
Центральная симметрия - отображение пространства на себя, при котором
любая точка М переходит в симметричную ей точку М1
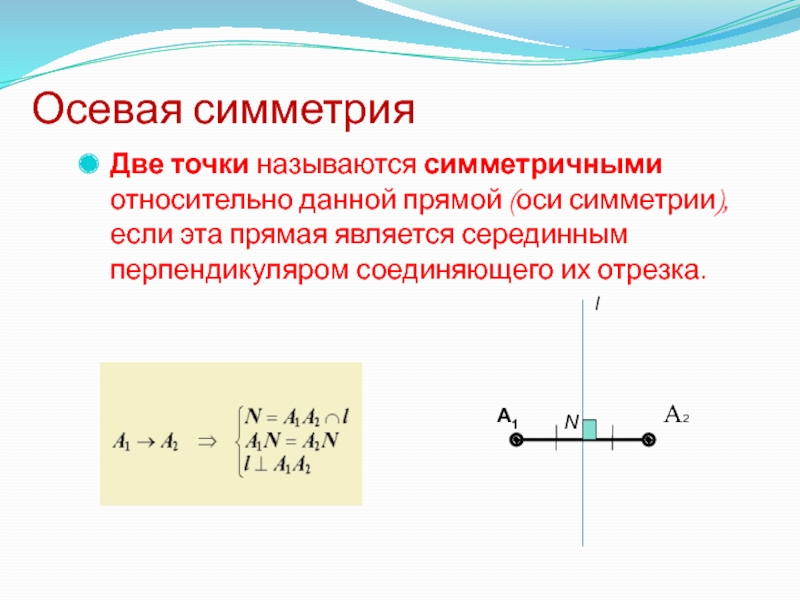
относительно данного центра О .Слайд 23Осевая симметрия
Две точки называются симметричными относительно данной прямой (оси симметрии),
если эта прямая является серединным перпендикуляром соединяющего их отрезка.
l
N
Слайд 24Осевой симметрией с осью l называется отображение пространства на себя,
при котором любая точка М переходит в симметричную ей точку
М1 относительно оси l.Слайд 25Фигура называется симметричной относительно прямой l, если для каждой точки
фигуры симметричная ей точка относительно прямой l также принадлежит этой
фигуре. Прямая l называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.l
Ф
Ф1
Слайд 36Симметрия в пространстве. Зеркальная симметрия.
При зеркальной симметрии каждая точка одной
фигуры переходит в симметричную ей точку другой фигуры относительно данной
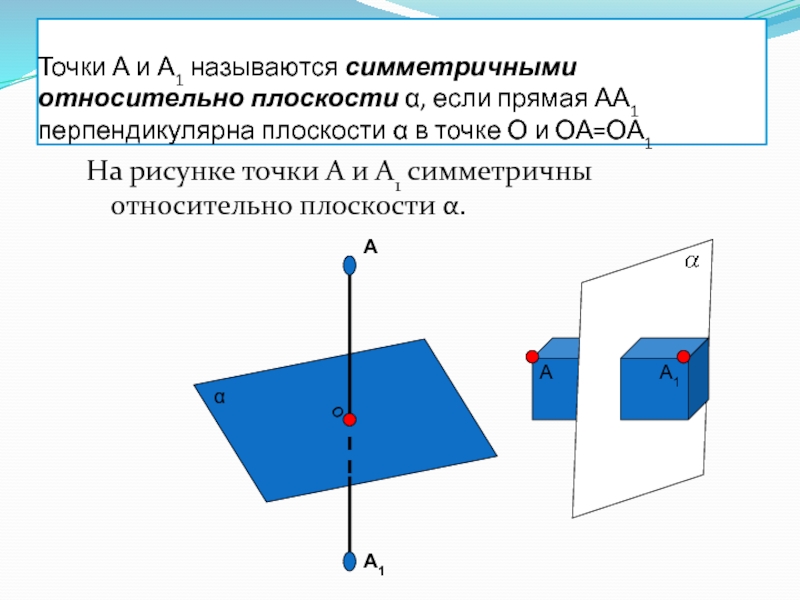
плоскости.Слайд 37Точки А и А1 называются симметричными относительно плоскости α, если
прямая АА1 перпендикулярна плоскости α в точке О и ОА=ОА1
На
рисунке точки А и А1 симметричны относительно плоскости α. о
А
А1
А
А1
α
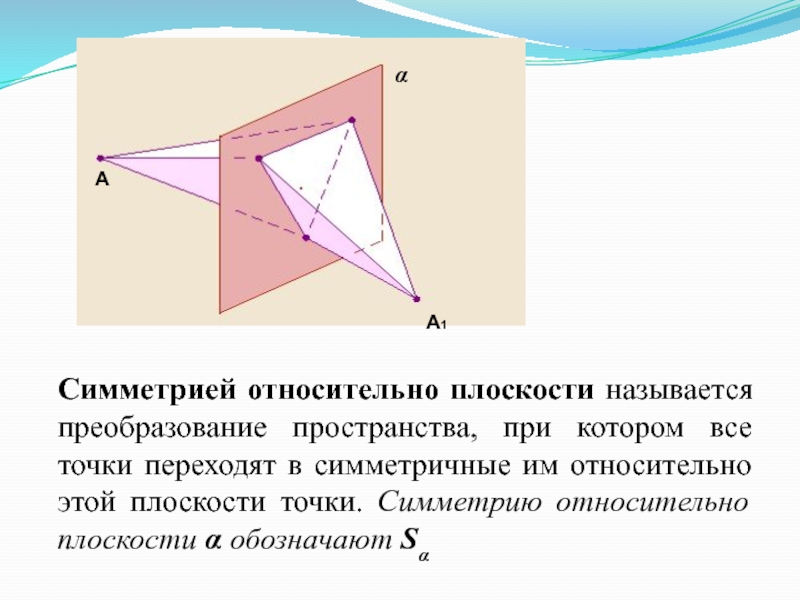
Слайд 38Симметрией относительно плоскости называется преобразование пространства, при котором все точки
переходят в симметричные им относительно этой плоскости точки. Симметрию относительно
плоскости α обозначают SαА
А1
α
Слайд 39Зеркальная симметрия является геометрическим преобразованием.
При зеркальной симметрии расстояния между соответствующими
точками фигур сохраняются.
Симметрия относительно плоскости является изометрией.
Каждая фигура при зеркальной
симметрии переходит в равную ей фигуру.Свойства симметрии относительно плоскости
Слайд 41
Отражение в воде – хороший пример зеркальной симметрии в
природе.
Мы любуемся пейзажами художников, удачными снимками. Горы красиво отражаются на
поверхности озера, придавая снимку законченность. Поверхность озера играет роль зеркала, и воспроизводит отражение с геометрической точностью. Поверхность воды есть плоскость симметрии...Слайд 43Симметрия – это идея, с помощью которой человек веками пытался
объяснить и создать порядок, красоту и совершенство.
(Герман Вейль-немецкий математик
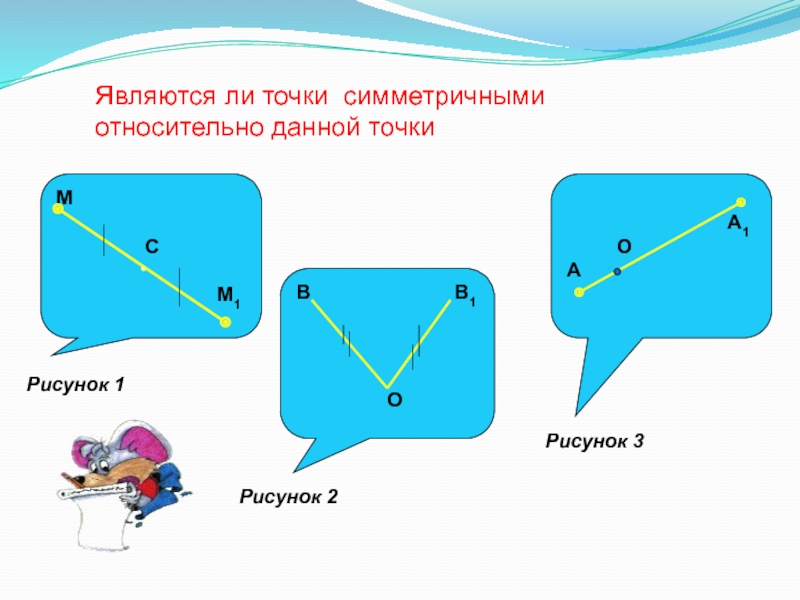
и физик, член Национальной Академии Наук США)Слайд 55Являются ли точки симметричными относительно данной точки
М
С
М1В В1
О
А1
О
А
Рисунок 1
Рисунок 2
Рисунок 3