Синус, косинус и тангенс в прямоугольном треугольнике

Содержание

1. Синус, косинус и тангенс в прямоугольном треугольнике
2. В папирусе Ахилеса часто встречается прямоугольный треугольник,
3. С самолета радируют на ледокол, что он
4. Помогите лилипуту определить рост Гулливера
5. Слайд 5
6. Слайд 6
7. АВ – гипотенузаВС – катет, противолежащий углу ААС – катет, прилежащий углу А
8. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.Синус (sin)
9. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.Косинус (cos)
10. Тангенс (tg)Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
11. Индийские математики синус обозначали словом "джива" (букв.
12. Задача Найдите синус, косинус и тангенс
13. ФИЗМИНУТКА
14. Чтобы сильным стать и ловким, Приступаем к
15. Слайд 15
16. Тригонометрические тождестваОсновное тригонометрическое тождество:2) Тангенс угла равен отношению синуса к косинусу этого угла.
17. Задача №593а) Найти sinα и tgα, если cosα=АВСб) Найти cosα и tgα,если sinα=
18. Если острый угол одного прямоугольного треугольника равен
19. Задание на дом: п. 66, в. 15-17, № 591(в, г), 593(б, г), 592* (а, б) .
20. С тригонометрией сейчасЗнакомы даже звери.Правила все говорятЧетко
21. Скачать презентанцию

В папирусе Ахилеса часто встречается прямоугольный треугольник, который занимает почетное место и в вавилонской геометрии. Землемеры и поныне прибегают к прямоугольному треугольнику для определения расстояний и т.п.Фалес решил найти высоту одной

Главная
Математика
Синус, косинус и тангенс в прямоугольном треугольнике

Слайды и текст этой презентации

Слайд 1
Синус, косинус и тангенс в прямоугольном треугольнике

Слайд 2В папирусе Ахилеса часто встречается прямоугольный треугольник, который занимает почетное

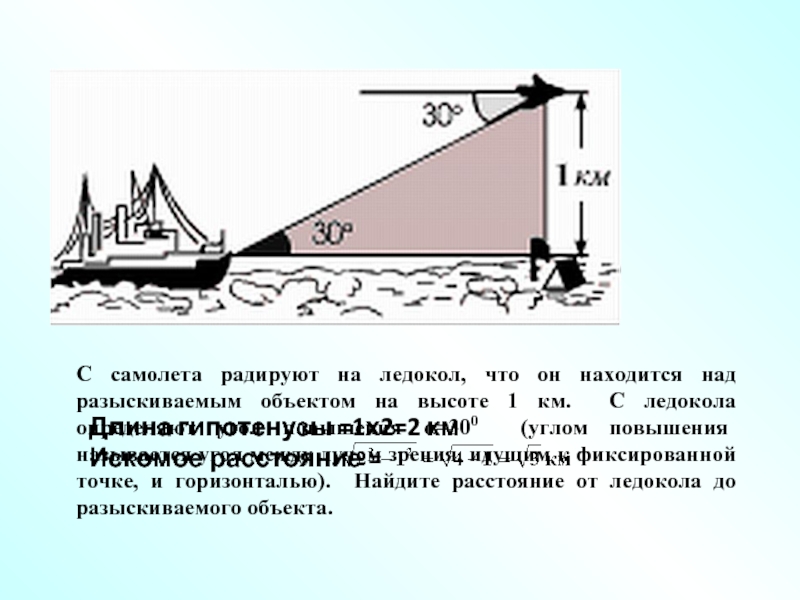
место и в вавилонской геометрии. Землемеры и поныне прибегают к

прямоугольному треугольнику для определения расстояний и т.п.

Фалес решил найти высоту одной из громадных пирамид. Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет той же длины, что и высота пирамиды».

В папирусе Ахилеса часто встречается прямоугольный треугольник, который занимает почетное место и в вавилонской геометрии. Землемеры и

Слайд 3С самолета радируют на ледокол, что он находится над разыскиваемым

объектом на высоте 1 км. С ледокола определяют угол повышения

α=300 (углом повышения называется угол между лучом зрения, идущим к фиксированной точке, и горизонталью). Найдите расстояние от ледокола до разыскиваемого объекта.

С самолета радируют на ледокол, что он находится над разыскиваемым объектом на высоте 1 км. С ледокола

Слайд 4Помогите лилипуту определить рост Гулливера

Слайд 5

Слайд 6

Слайд 7

АВ – гипотенуза
ВС – катет, противолежащий углу А
АС – катет,

прилежащий углу А

Слайд 8
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к

гипотенузе.
Синус (sin)

Слайд 9

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к

гипотенузе.
Косинус (cos)

Слайд 10
Тангенс (tg)
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета

к прилежащему.

Слайд 11Индийские математики синус обозначали словом "джива" (букв. - тетива лука).

Арабы переделали этот термин в "джиба", который в дальнейшем превратился

в "джайо" - обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus.

Тангенс (от лат. tangens - касающийся)

Из истории терминов

Индийские математики синус обозначали словом

Слайд 12Задача
Найдите синус, косинус и тангенс острого угла А

прямоугольного треугольника с катетами 8 см и 25 см.
А
С
В
25

Задача Найдите синус, косинус и тангенс острого угла А прямоугольного треугольника с катетами 8 см и

Слайд 13ФИЗМИНУТКА

Слайд 14Чтобы сильным стать и ловким, Приступаем к тренировке. Носом вдох, а выдох

ртом. Дышим глубже, а потом Шаг на месте, не спеша. Как погода хороша! Мы

проверили осанку И свели лопатки. Мы походим на носках, И идём на пятках.

ФИЗМИНУТКА НА УРОКЕ –
ЗДОРОВЬЕ НА ГОДЫ!

Чтобы сильным стать и ловким, Приступаем к тренировке. Носом вдох, а выдох ртом. Дышим глубже, а потом

Слайд 15

Слайд 16Тригонометрические тождества
Основное тригонометрическое тождество:

2) Тангенс угла равен отношению синуса к

косинусу этого угла.

Слайд 17
Задача №593
а) Найти sinα и tgα, если cosα=
А
В
С
б) Найти cosα

и tgα,
если sinα=

Слайд 18

Если острый угол одного прямоугольного треугольника равен острому углу другого

прямоугольного треугольника, то синусы этих углов равны; то же верно

для косинусов и тангенсов.

Доказательство:

Синус, косинус, тангенс острого угла
прямоугольного треугольника

Дано: ∠A = ∠A1

∠A = ∠A1 ⇒

Δ ABC ~ Δ A1B1C1 ⇒

Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны;

Слайд 19Задание на дом:
п. 66, в. 15-17, № 591(в, г),

593(б, г), 592* (а, б) .

Слайд 20С тригонометрией сейчас
Знакомы даже звери.
Правила все говорят
Четко и уверенно.
И попросим

мы зверят
Рассказать их для ребят.
Как мы косинус считаем,
Ты спроси медузу.
—

Делим прилежащий катет
На гипотенузу.
Синус вычислить сумеет
Зверь любой из чащи:
На гипотенузу делит
Катет противолежащий.
Чтобы тангенс получить,
Нужно катеты делить.
Вы в числителе берете
Тот, что для угла напротив.
Тот, который прилежит,
В знаменателе пиши.

С тригонометрией сейчасЗнакомы даже звери.Правила все говорятЧетко и уверенно.И попросим мы зверятРассказать их для ребят.Как мы косинус

Скачать презентацию

Теги

Разделы презентаций