Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синус, косинус, тангенс угла
Содержание
- 1. Синус, косинус, тангенс угла
- 2. Тема: Определение синуса, косинуса, тангенса и котангенса.
- 3. Цели урока:1.Знать определение синуса, косинуса, тангенса и
- 4. План урокаИстория развития тригонометрии.Повторение курса геометрии.Изучение нового материала.Закрепление
- 5. Историческая справка
- 6. Древний Вавилон-умели предсказывать солнечные и лунные затмения.Древнегреческие
- 7. Большой вклад в развитие тригонометрии внесли:ГиппархПтолемейФрансуа ВиетЭйлерБернулли
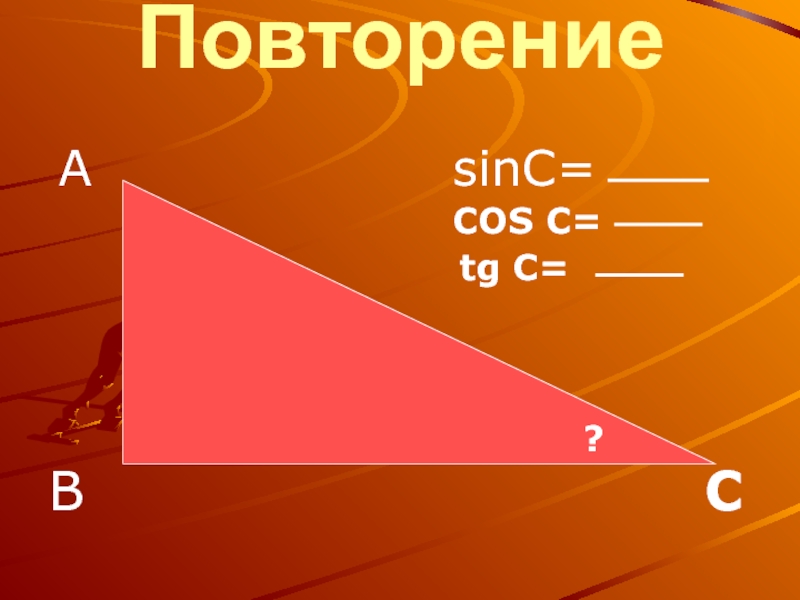
- 8. Повторение А
- 9. ПовторениеДля единичной полуокружности
- 10. ПовторениеОсновное тригонометрическое тождество:SIN2 X+COS2 Х=1
- 11. уухАО
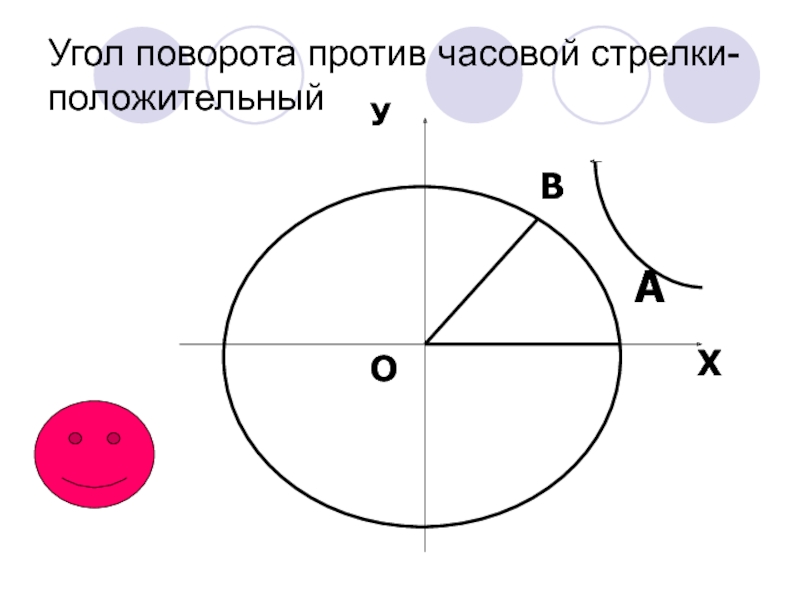
- 12. Угол поворота против часовой стрелки- положительныйАОВУХ
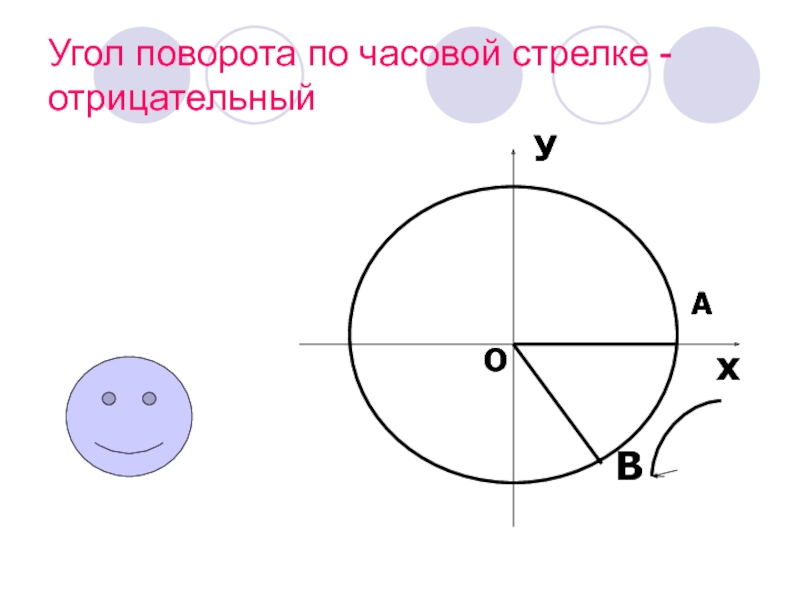
- 13. Угол поворота по часовой стрелке - отрицательныйОхУАВ
- 14. Угол поворотаПоложительный
- 15. Из курса геометрии известно: Мера угла в
- 16. Ответь на вопрос:Каким числом может выражаться в градусах угол поворота?
- 17. В Ы В О Д: Угол поворота
- 18. Рассмотрим примеры
- 19. В Ы В О Д Существует бесконечно
- 20. З А П О М Н И00
- 21. В ы в о д: Эти углы
- 22. Углом какой четверти является угол β,если: β=1670 β=2870 β=-650
- 23. Стр.153.- определение.
- 24. Лабораторная работа
- 25. В
- 26. ЗапомниSinα, Cosα-определены при любом α. Почему?
- 27. Стр.154 При каком α tgα не определён?Почему?
- 28. sinα , cosα , tgα , ctgα –называют тригонометрическими функциями.
- 29. Для единичной окружности:Область значения синуса и косинуса
- 30. Найти синус, косинус,тангенс и котангенс 2700Проверьте решение на стр.156
- 31. Устно№ 699№701
- 32. Письменно№705Используй таблицу стр.155
- 33. Скачать презентанцию
Тема: Определение синуса, косинуса, тангенса и котангенса.
Слайды и текст этой презентации
Слайд 3Цели урока:
1.Знать определение синуса, косинуса, тангенса и котангенса.
2.Уметь применять эти
определения к решению примеров и задач.
Слайд 4План урока
История развития тригонометрии.
Повторение курса геометрии.
Изучение нового материала.
Закрепление
Слайд 6
Древний Вавилон-умели предсказывать солнечные и лунные затмения.
Древнегреческие учёные-составили таблицы хорд(первые
тригонометрические таблицы)
Учёные Индии и Ближнего Востока-положили начало радианной мере угла.
Слайд 9Повторение
Для единичной полуокружности
y
у
SIN A = = Y
R
X
COS A= = X
R
0 ≤SIN A≤ 1
-1 ≤ COS A ≤1
х
А
В
1
-1
1
Слайд 17В Ы В О Д: Угол поворота может выражаться в градусах
каким угодно действительным числом от -∞ до +∞
Слайд 19В Ы В О Д Существует бесконечно много углов поворота, при
которых начальный радиус ОА переходит в радиус ОВ.
В зависимости от
того, в какой координатной четверти окажется радиус ОВ, угол α называют углом этой четверти.
Слайд 21В ы в о д: Эти углы не относятся ни к
какой четверти.
00 ,± 900 ,± 1800 ,
± 2700 ,± 3600....
Слайд 25 В Ы В О
Д:
Синус, косинус, тангенс и котангенс не зависят от радиуса.
Вычертите
три окружности произвольного радиуса с центром в начале координат.Постройте начальный радиус ОА.
Поверните начальный радиус на угол α=450
В каждом из случаев найдите SIN 450.
(смотри пример 1. стр.154.)
Какой получился результат? Сделай вывод..
Слайд 29Для единичной окружности:
Область значения синуса и косинуса есть промежуток
[-1;1]
Область значения тангенса и котангенса есть множество всех
действительных чисел.![Для единичной окружности:Область значения синуса и косинуса есть промежуток [-1;1]Область значения тангенса и котангенса](/img/tmb/5/473888/111b6b94561cef3bbee2defdfc252043-800x.jpg "Синус, косинус, тангенс угла Для единичной окружности:Область значения синуса и косинуса есть промежуток [-1;1]Область")
