Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Стереометрия"
Содержание
- 1. "Стереометрия"
- 2. СодержаниеСтереометрияАксиомы стереометрии
- 3. Стереометрия Курс геометрии состоит
- 4. В отличие от реальных предметов геометрические тела,
- 5. Аксиомы стереометрии В планиметрии основными фигурами были
- 6. А1. Через любые три точки, не лежащие
- 7. А2. Если две точки прямой лежат в
- 8. А3. Если две плоскости имеют общую
- 9. Тела вращения
- 10. Цилиндр По построению концы образующих, расположенные
- 11. Цилиндр может быть получен вращением прямоугольника вокруг
- 12. Объем цилиндра равен произведению площади основания на
- 13. Конус Рассмотрим окружность L с центром О и
- 14. Конус может быть получен вращением прямоугольного треугольника
- 15. За площадь боковой поверхности конуса принимается площадь
- 16. Усеченный конус Усеченный конус может быть получен вращением
- 17. Объем усеченного конуса равенПлощадь боковой поверхности усеченного
- 18. Сфера и шар Сферой называется поверхность, состоящая из
- 19. Объем шара радиуса R равенПлощадь сферы радиуса
- 20. Многогранники
- 21. Многогранник - геометрическое тело, ограниченное со всех
- 22. ТетраэдрТетраэдр – треугольная пирамида; правильный тетраэдр ограничен
- 23. Объем тетраэдра равен:Площадь полной поверхности тетраэдра вычисляется по формуле:Где а – сторона тетраэдра
- 24. Куб или гексаэдрКуб или правильный гексаэдр –
- 25. Объем куба равенПлощадь поверхности куба вычисляется по формуле Где а – сторона куба
- 26. ОктаэдрОктаэдр – восьмигранник;
- 27. Объем октаэдра вычисляется по формулеПлощадь поверхности октаэдра равнаГде а – сторона октаэдра
- 28. ДодекаэдрДодекаэдр – двенадцатигранник; тело,
- 29. Площадь поверхности додекаэдра вычисляется по формулеОбъем додекаэдра равенГде а – сторона додекаэдра
- 30. ИкосаэдрИкосаэдр – двадцатигранник;
- 31. Объем икосаэдра равенПлощадь поверхности икосаэдра вычисляется по формулеГде а – сторона икосаэдра
- 32. Правильные многогранники иногда называют Платоновыми телами, поскольку
- 33. Тетраэдр олицетворял огонь, поскольку его вершина устремлена
- 34. Призма Многогранник, составленный из двух равных многоугольников А1А2...Аn
- 35. Площадью полной поверхности призмы называется
- 36. Пирамида Многогранник, составленный из n-угольника А1А2...Аn и n
- 37. Площадью полной поверхности пирамиды называется сумма площадей
- 38. ЛитератураПогорелов А.В. «Геометрия 7-11 кл.»Электронное издание «Геометрия
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Стереометрия
Подготовила:
Учитель математики
Харченко Наталья Анатольевна
Алматы 2014 г.
Министерство образования и науки РК
КГУ
«Общеобразовательная школа №20»
Слайд 2Содержание
Стереометрия
Аксиомы стереометрии
Аксиома
1
Аксиома 2Аксиома 3
Тела вращения
Цилиндр
Конус
Усеченный конус
Сфера и шар
Многогранники
Тетраэдр
Куб или гексаэдр
Октаэдр
Додекаэдр
Икосаэдр
Призма
Пирамида
Литература
Слайд 3Стереометрия
Курс геометрии состоит из двух частей:
планиметрии и стереометрии. В планиметрии изучаются свойства геометрических фигур на
плоскости. Стереометрия - это раздел геометрии, в котором изучаются свойства фигур в пространстве.Слово “стереометрия” происходит от греческих слов “стереос”-объемный, пространственный и “метрео” - измерять. Простейшими и, можно сказать, основными фигурами в пространстве являются точки, прямые и плоскости. Наряду с этими фигурами мы рассматриваем так называемые геометрические тела и их поверхности. Представление о геометрических телах дают окружающие нас предметы. Так, например, кристаллы имеют форму геометрических тел, поверхности которых составлены из многоугольников. Такие поверхности называются многогранниками.
Одним из простейших многогранников является куб.
Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром. Такую же форму имеет футбольный мяч.
Консервная банка имеет форму геометрического тела, называемого цилиндром.
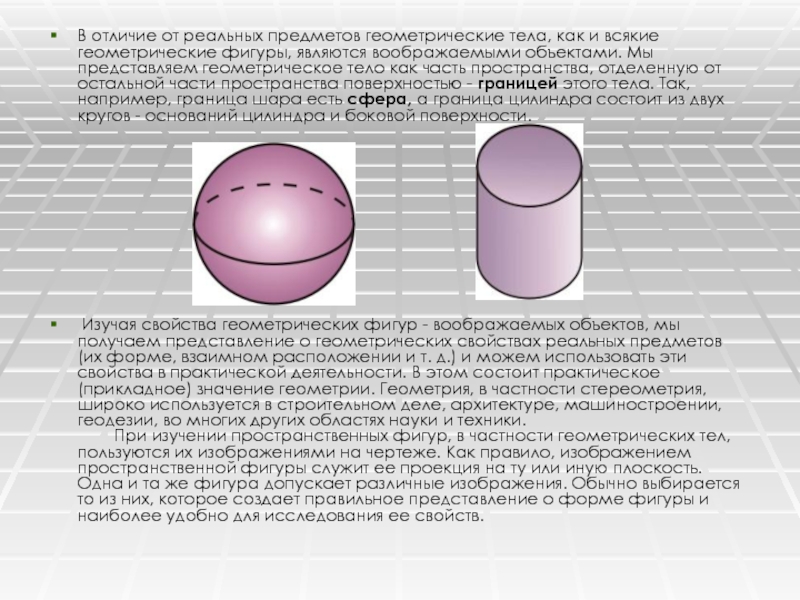
Слайд 4В отличие от реальных предметов геометрические тела, как и всякие
геометрические фигуры, являются воображаемыми объектами. Мы представляем геометрическое тело как
часть пространства, отделенную от остальной части пространства поверхностью - границей этого тела. Так, например, граница шара есть сфера, а граница цилиндра состоит из двух кругов - оснований цилиндра и боковой поверхности.Изучая свойства геометрических фигур - воображаемых объектов, мы получаем представление о геометрических свойствах реальных предметов (их форме, взаимном расположении и т. д.) и можем использовать эти свойства в практической деятельности. В этом состоит практическое (прикладное) значение геометрии. Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники. При изучении пространственных фигур, в частности геометрических тел, пользуются их изображениями на чертеже. Как правило, изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения. Обычно выбирается то из них, которое создает правильное представление о форме фигуры и наиболее удобно для исследования ее свойств.
Слайд 5Аксиомы стереометрии
В планиметрии основными фигурами были точки и прямые.
В стереометрии наряду с ними рассматривается еще одна основная фигура
- плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.Как и в планиметрии, точки обозначаются прописными латинскими буквами А, В, С и т. д., а прямые - строчными латинскими буквами а, b, с и т. д. или двумя большими латинскими буквами АВ, CD и т. д. Плоскости обозначаются греческими буквами α, β, γ и т. д. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области.
Ясно, что в каждой плоскости лежат какие-то точки пространства,
но не все точки пространства лежат в одной и той же плоскости.
На рисунке точки А и В лежат в плоскости β (плоскость β проходит
через эти точки), а точки М, N, Р не лежат в этой плоскости.
Коротко это записывают так: А β, В β, М β; Х β; Р β;. Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, большая часть которых нам знакома по курсу планиметрии.
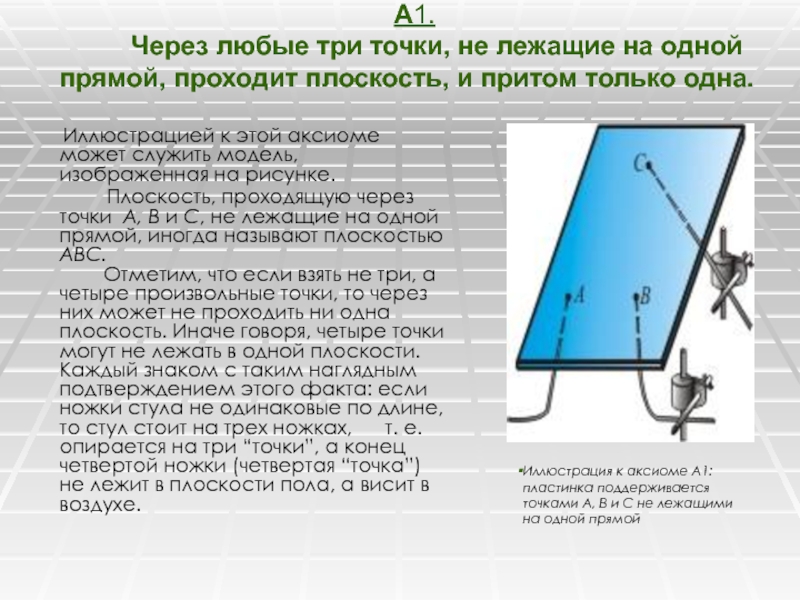
Слайд 6 А1. Через любые три точки, не лежащие на одной прямой, проходит
плоскость, и притом только одна.
Иллюстрацией к этой аксиоме
может служить модель, изображенная на рисунке.Плоскость, проходящую через точки А, В и С, не лежащие на одной прямой, иногда называют плоскостью АВС. Отметим, что если взять не три, а четыре произвольные точки, то через них может не проходить ни одна плоскость. Иначе говоря, четыре точки могут не лежать в одной плоскости. Каждый знаком с таким наглядным подтверждением этого факта: если ножки стула не одинаковые по длине, то стул стоит на трех ножках, т. е. опирается на три “точки”, а конец четвертой ножки (четвертая “точка”) не лежит в плоскости пола, а висит в воздухе.
Иллюстрация к аксиоме А1:
пластинка поддерживается
точками A, B и C не лежащими
на одной прямой
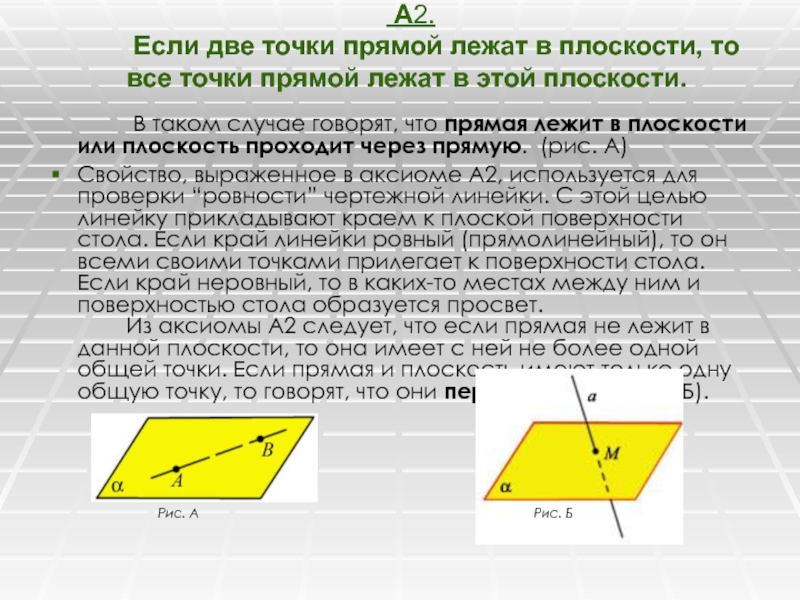
Слайд 7 А2. Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
В таком случае говорят, что прямая
лежит в плоскости или плоскость проходит через прямую. (рис. А) Свойство, выраженное в аксиоме А2, используется для проверки “ровности” чертежной линейки. С этой целью линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный (прямолинейный), то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет. Из аксиомы А2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются (рис. Б).
Рис. А Рис. Б
Слайд 8 А3. Если две плоскости имеют общую точку, то они имеют общую
прямую, на которой лежат все общие точки этих плоскостей.
В таком
случае говорят, что плоскости, пересекаются по прямой (рис. В). Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка комнаты.
В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии. Более того, признаки равенства и подобия треугольников, известные из курса планиметрии, справедливы и для треугольников, расположенных в разных плоскостях.
Рис. В
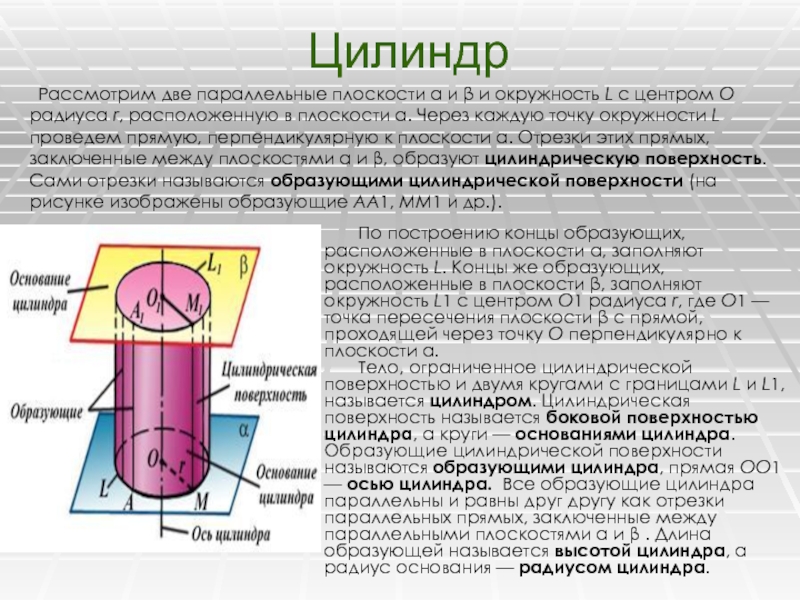
Слайд 10Цилиндр
По построению концы образующих, расположенные в плоскости α,
заполняют окружность L. Концы же образующих, расположенные в плоскости β,
заполняют окружность L1 с центром О1 радиуса r, где О1 — точка пересечения плоскости β с прямой, проходящей через точку О перпендикулярно к плоскости α. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги — основаниями цилиндра. Образующие цилиндрической поверхности называются образующими цилиндра, прямая ОО1 — осью цилиндра. Все образующие цилиндра параллельны и равны друг другу как отрезки параллельных прямых, заключенные между параллельными плоскостями α и β . Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра. Рассмотрим две параллельные плоскости α и β и окружность L с центром О радиуса r, расположенную в плоскости α. Через каждую точку окружности L проведем прямую, перпендикулярную к плоскости α. Отрезки этих прямых, заключенные между плоскостями α и β, образуют цилиндрическую поверхность. Сами отрезки называются образующими цилиндрической поверхности (на рисунке изображены образующие AA1, ММ1 и др.).
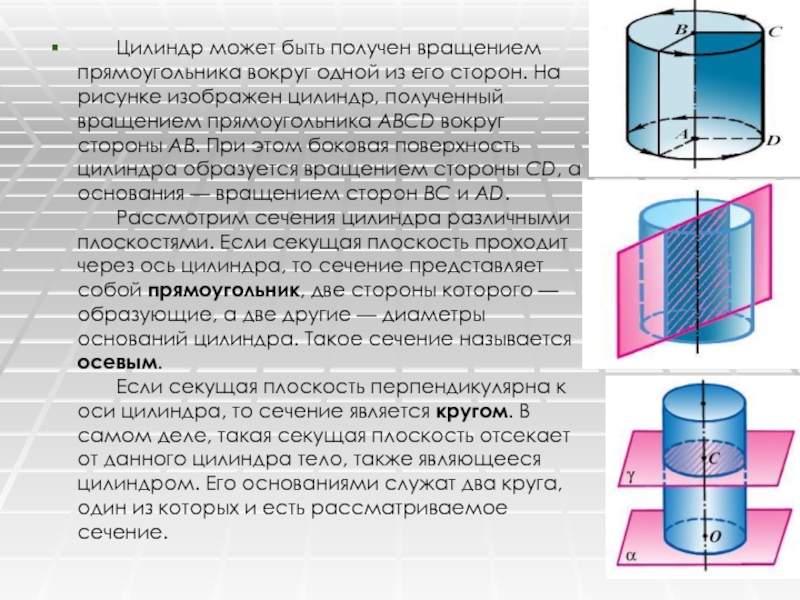
Слайд 11 Цилиндр может быть получен вращением прямоугольника вокруг одной из его
сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника ABCD вокруг
стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны CD, а основания — вращением сторон ВС и AD. Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого — образующие, а две другие — диаметры оснований цилиндра. Такое сечение называется осевым. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.Слайд 12
Объем цилиндра равен произведению площади основания на высоту
Площадь боковой поверхности
цилиндра вычисляется по формуле
Где R –
радиус цилиндра, h – его высота.
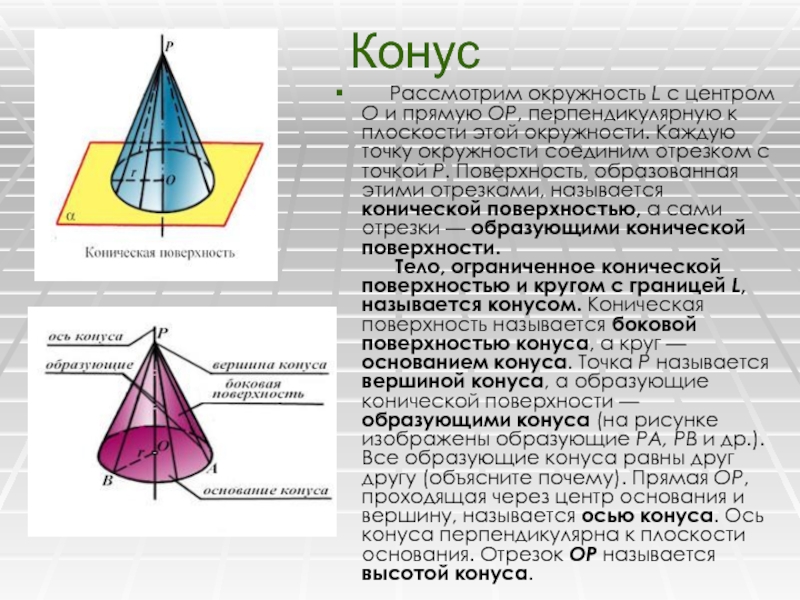
Слайд 13Конус
Рассмотрим окружность L с центром О и прямую ОP, перпендикулярную
к плоскости этой окружности. Каждую точку окружности соединим отрезком с
точкой Р. Поверхность, образованная этими отрезками, называется конической поверхностью, а сами отрезки — образующими конической поверхности. Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг — основанием конуса. Точка Р называется вершиной конуса, а образующие конической поверхности — образующими конуса (на рисунке изображены образующие РА, РВ и др.). Все образующие конуса равны друг другу (объясните почему). Прямая ОР, проходящая через центр основания и вершину, называется осью конуса. Ось конуса перпендикулярна к плоскости основания. Отрезок ОР называется высотой конуса.Слайд 14 Конус может быть получен вращением прямоугольного треугольника вокруг одного из
его катетов. На рисунке изображен конус, полученный вращением прямоугольного треугольника
ABC вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС.Рассмотрим сечение конуса различными плоскостями. Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого — диаметр основания конуса, а боковые стороны — образующие конуса. Это сечение называется осевым.
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О1 , расположенным на оси конуса. Радиус r1 этого круга равен r, где r — радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1.
Слайд 15За площадь боковой поверхности конуса принимается площадь его развертки.
Площадь
боковой поверхности конуса вычисляется по формуле
Объем конуса равен одной трети
произведения площади основания на высотуГде R – радиус основания конуса, h – его высота, l – длина образующей.
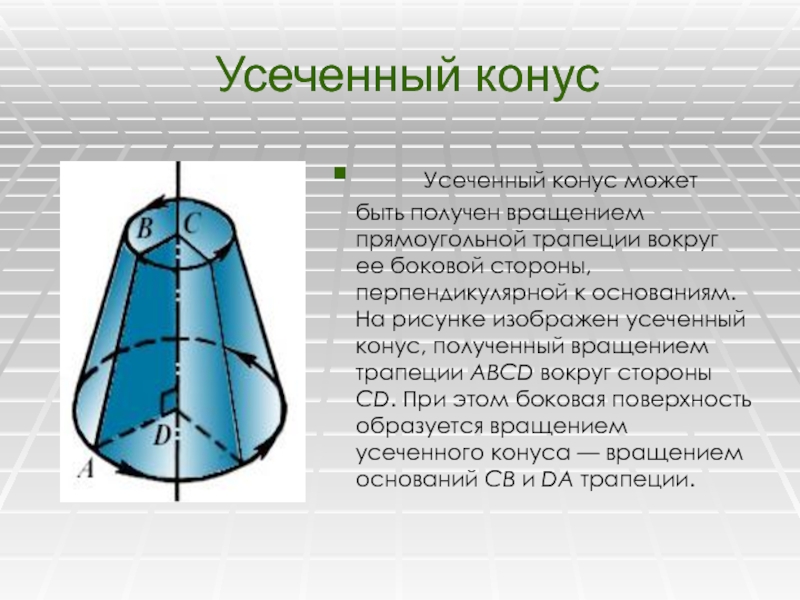
Слайд 16Усеченный конус
Усеченный конус может быть получен вращением прямоугольной трапеции вокруг
ее боковой стороны, перпендикулярной к основаниям. На рисунке изображен усеченный
конус, полученный вращением трапеции ABCD вокруг стороны CD. При этом боковая поверхность образуется вращением усеченного конуса — вращением оснований CB и DA трапеции.Слайд 17Объем усеченного конуса равен
Площадь боковой поверхности усеченного конуса вычисляется по
формуле
Где R, r – радиусы оснований,
l – длина
образующей, h – его высота
Слайд 18Сфера и шар
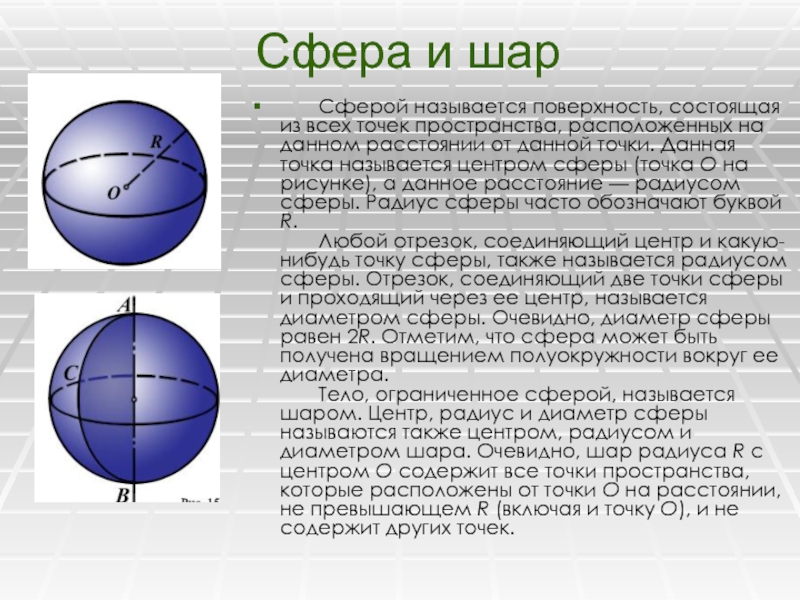
Сферой называется поверхность, состоящая из всех точек пространства,
расположенных на данном расстоянии от данной точки. Данная точка называется центром
сферы (точка О на рисунке), а данное расстояние — радиусом сферы. Радиус сферы часто обозначают буквой R. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Очевидно, диаметр сферы равен 2R. Отметим, что сфера может быть получена вращением полуокружности вокруг ее диаметра. Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Очевидно, шар радиуса R с центром О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R (включая и точку О), и не содержит других точек.Слайд 19 Объем шара радиуса R равен
Площадь сферы радиуса R вычисляется по
формуле
Где R – радиус сферы
Слайд 21Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками,
называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер
— вершинами многогранника. По числу граней различают четырехгранники, пятигранники и т. д. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней. Выпуклый многогранник называется правильным, если все его грани — одинаковые правильные многоугольники и все многогранные углы при вершинах равны. Существует 5 видов правильных многогранников: тетраэдр, куб (гексаэдр), октаэдр, додекаэдр, икосаэдр.Слайд 22Тетраэдр
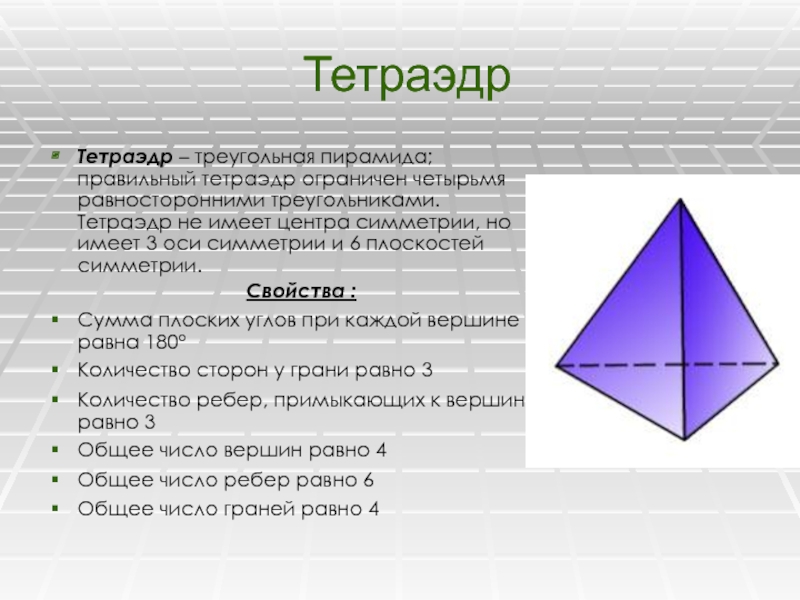
Тетраэдр – треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии
и 6 плоскостей симметрии.Свойства :
Сумма плоских углов при каждой вершине равна 180º
Количество сторон у грани равно 3
Количество ребер, примыкающих к вершине равно 3
Общее число вершин равно 4
Общее число ребер равно 6
Общее число граней равно 4
Слайд 23Объем тетраэдра равен:
Площадь полной поверхности тетраэдра вычисляется по формуле:
Где а
– сторона тетраэдра
Слайд 24Куб или гексаэдр
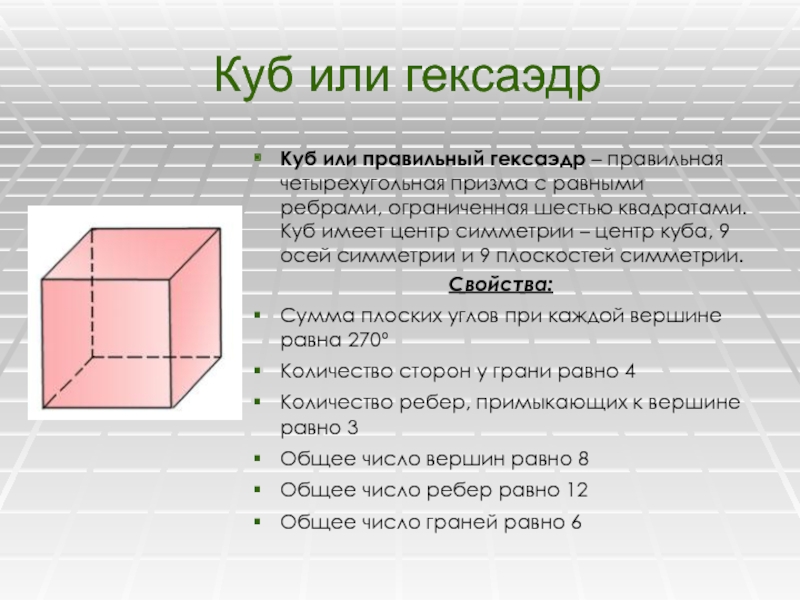
Куб или правильный гексаэдр – правильная четырехугольная призма
с равными ребрами, ограниченная шестью квадратами. Куб имеет центр симметрии
– центр куба, 9 осей симметрии и 9 плоскостей симметрии.Свойства:
Сумма плоских углов при каждой вершине равна 270º
Количество сторон у грани равно 4
Количество ребер, примыкающих к вершине равно 3
Общее число вершин равно 8
Общее число ребер равно 12
Общее число граней равно 6
Слайд 26Октаэдр
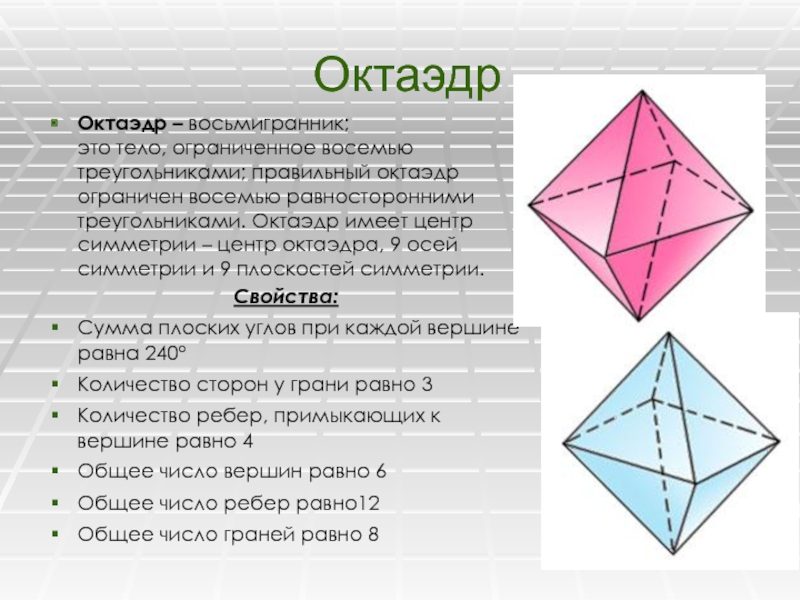
Октаэдр – восьмигранник;
это тело, ограниченное восемью
треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками. Октаэдр имеет центр симметрии – центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.Свойства:
Сумма плоских углов при каждой вершине равна 240º
Количество сторон у грани равно 3
Количество ребер, примыкающих к вершине равно 4
Общее число вершин равно 6
Общее число ребер равно12
Общее число граней равно 8
Слайд 27Объем октаэдра вычисляется по формуле
Площадь поверхности октаэдра равна
Где а –
сторона октаэдра
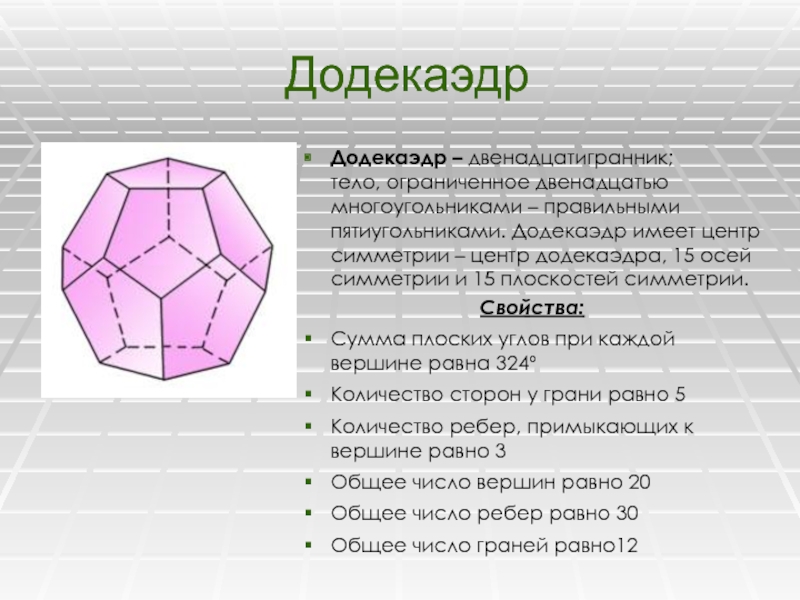
Слайд 28Додекаэдр
Додекаэдр – двенадцатигранник; тело, ограниченное двенадцатью многоугольниками
– правильными пятиугольниками. Додекаэдр имеет центр симметрии – центр додекаэдра,
15 осей симметрии и 15 плоскостей симметрии.Свойства:
Сумма плоских углов при каждой вершине равна 324º
Количество сторон у грани равно 5
Количество ребер, примыкающих к вершине равно 3
Общее число вершин равно 20
Общее число ребер равно 30
Общее число граней равно12
Слайд 29Площадь поверхности додекаэдра вычисляется по формуле
Объем додекаэдра равен
Где а –
сторона додекаэдра
Слайд 30Икосаэдр
Икосаэдр – двадцатигранник;
тело, ограниченное двадцатью многоугольниками, правильный икосаэдр ограничен двадцатью равносторонними треугольниками.
Икосаэдр имеет центр симметрии – центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.Свойства:
Сумма плоских углов при каждой вершине равна 300º
Количество сторон у грани равно 3
Количество ребер, примыкающих к вершине равно 5
Общее число вершин равно 20
Общее число ребер равно 30
Общее число граней равно20
Слайд 31Объем икосаэдра равен
Площадь поверхности икосаэдра вычисляется по формуле
Где а –
сторона икосаэдра
Слайд 32
Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное
место в философской картине мира, разработанной великим мыслителем Древней Греции
Платоном.Платон считал, что мир состоит из четырех «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырех правильных многогранников.
Слайд 33Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у
разгоревшегося пламени.
Икосаэдр, как самый обтекаемый, воду.
Куб, самая устойчивая из фигур,
землю.Октаэдр – воздух.
В наше время эту систему можно сравнить с четырьмя состояниями вещества – твердым, жидким, газообразным и пламенным.
Пятый многогранник - додекаэдр символизировал весь мир (пятый элемент) и почитался главнейшим.
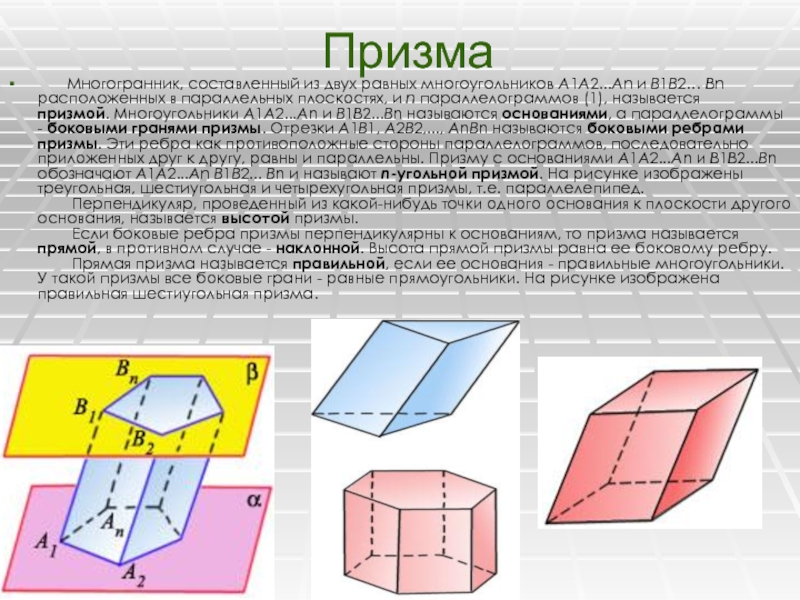
Слайд 34Призма
Многогранник, составленный из двух равных многоугольников А1А2...Аn и В1В2… Вn
расположенных в параллельных плоскостях, и n параллелограммов (1), называется призмой. Многоугольники
А1А2...Аn и B1B2...Вn называются основаниями, а параллелограммы - боковыми гранями призмы. Отрезки А1B1, A2B2,..., АnВn называются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограммов, последовательно приложенных друг к другу, равны и параллельны. Призму с основаниями А1А2...Аn и B1B2...Вn обозначают А1А2...Аn B1B2... Вn и называют n-угольной призмой. На рисунке изображены треугольная, шестиугольная и четырехугольная призмы, т.е. параллелепипед. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае - наклонной. Высота прямой призмы равна ее боковому ребру. Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани - равные прямоугольники. На рисунке изображена правильная шестиугольная призма.Слайд 35 Площадью полной поверхности призмы называется сумма площадей всех
ее граней, а площадью боковой поверхности призмы - сумма площадей
ее боковых граней.где Р – периметр основания призмы, l – длина боковых ребер
Площадь Sполн полной поверхности выражается через площадь Sбок боковой поверхности и площадь Sосн основания призмы формулой
Объем призмы равен
Где S – площадь основания, h - высота
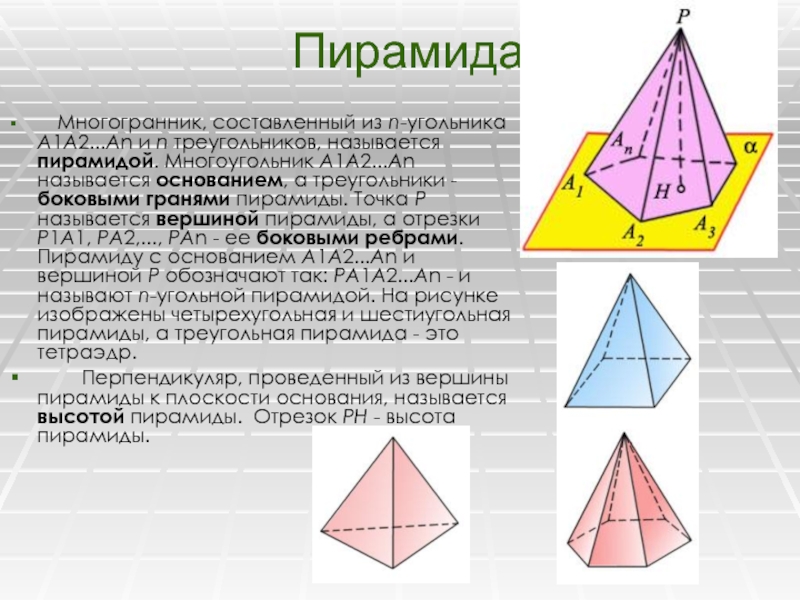
Слайд 36Пирамида
Многогранник, составленный из n-угольника А1А2...Аn и n треугольников, называется пирамидой.
Многоугольник А1А2...Аn называется основанием, а треугольники - боковыми гранями пирамиды.
Точка Р называется вершиной пирамиды, а отрезки Р1А1, РА2,..., РАn - ее боковыми ребрами. Пирамиду с основанием А1А2...Аn и вершиной Р обозначают так: РА1А2...Аn - и называют n-угольной пирамидой. На рисунке изображены четырехугольная и шестиугольная пирамиды, а треугольная пирамида - это тетраэдр.Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. Отрезок РН - высота пирамиды.
Слайд 37 Площадью полной поверхности пирамиды называется сумма площадей всех ее граней
(т.е. основания и боковых граней), а площадью боковой поверхности пирамиды
- сумма площадей ее боковых граней.Объем пирамиды равен
где S – площадь основания, h - высота
Слайд 38Литература
Погорелов А.В. «Геометрия 7-11 кл.»
Электронное издание «Геометрия 10» 2008 г.
Электронное
издание «Геометрия 11» 2008 г.
Электронное издание «Большая энциклопедия Кирилла и
Мефодия», 2008 г.Электронное издание «Activstudio 3»