Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства функций.
Содержание
- 1. Свойства функций.
- 2. Функция – зависимость одной переменной от другой,
- 3. СВОЙСТВА ФУНКЦИИ
- 4. План исследования функцииОбласть определенияМонотонностьОграниченностьНаибольшее, наименьшее значение НепрерывностьОбласть
- 5. Термины «возрастающая» и «убывающая» функции объединяют общим
- 6. Монотонность ВозрастающаяФункцию у = f(х) называют
- 7. ПРИМЕР № 1.Исследовать на монотонность функцию у = – 3х + 7.
- 8. ОграниченностьФункцию у = f(х) называют ограниченной снизу
- 9. ОПРЕДЕЛЕНИЕЧисло m называется наименьшим значением функции у
- 10. ОПРЕДЕЛЕНИЕ Число m называется наибольшим значением функции
- 11. НепрерывностьНепрерывность функции на промежутке Х означает, что
- 12. ВыпуклостьФункция выпукла вниз
- 13. Перечислите свойства функции:Область определенияМонотонностьОграниченностьНаибольшее, наименьшее значение Непрерывность
- 14. 1. Д (f) : [- 2;
- 15. Тестирование 1. На одном из рисунков изображен
- 16. Тестирование 2 На одном из рисунков изображен
- 17. Тестирование 3. На рисунке изображен график
- 18. Тестирование 4. Используя график функции у =
- 19. Тестирование 5. Используя график функции у =
- 20. ПРОВЕРЬ СЕБЯ Какое число у вас получилось? 12412
- 21. № 10.14Область определенияМонотонностьОграниченностьНаибольшее, наименьшее значение НепрерывностьОбласть значенияВыпуклость
- 22. ПРОВЕРЬ СЕБЯ 1.. Д (f) :
- 23. СПАСИБО ЗА УРОК!
- 24. Скачать презентанцию
Функция – зависимость одной переменной от другой, причем для любых значений х соответствует единственное значение функции y. График функции – множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а
Слайды и текст этой презентации
Слайд 2 Функция – зависимость одной переменной от другой, причем для любых
значений х соответствует единственное значение
функции y.
График функции –
множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты соответствующим значениям функции. Определение
Слайд 4План исследования функции
Область определения
Монотонность
Ограниченность
Наибольшее, наименьшее значение
Непрерывность
Область значения
Выпуклость
Слайд 5
Термины «возрастающая» и «убывающая» функции объединяют общим названием монотонная функция.
Исследование
функции на возрастание или убывание называют исследованием функции на монотонность.
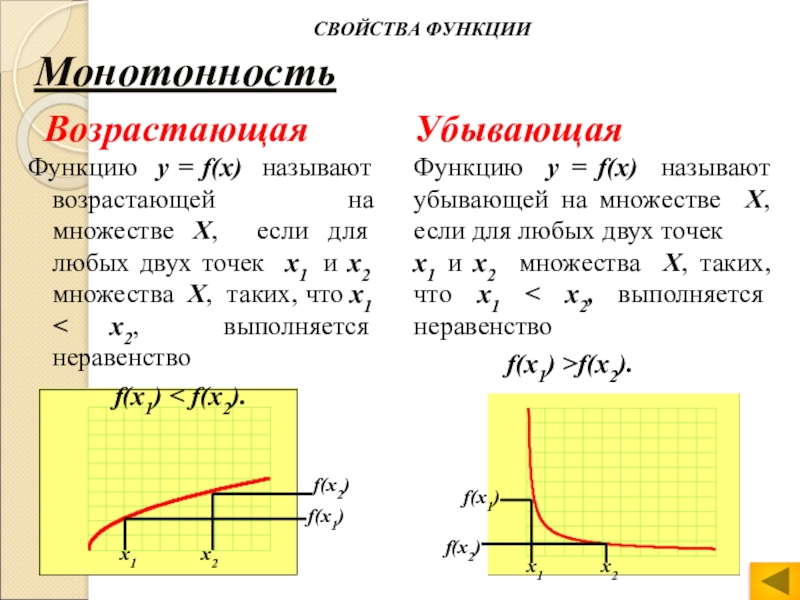
Слайд 6Монотонность
Возрастающая
Функцию у = f(х) называют возрастающей
на множестве Х, если для любых двух точек х1 и
х2 множества Х, таких, что х1 < х2, выполняется неравенствоf(х1) < f(х2).
Убывающая
Функцию у = f(х) называют убывающей на множестве Х, если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство
f(х1) >f(х2).
x1
x2
f(x1)
f(x2)
х1
x2
f(x2)
f(x1)
СВОЙСТВА ФУНКЦИИ
Слайд 8Ограниченность
Функцию у = f(х) называют ограниченной снизу на множестве Х,
если все значения функции на множестве Х больше некоторого числа.
Функцию
у = f(х) называют ограниченной сверху на множестве Х, если все значения функции на множестве Х меньше некоторого числа.х
у
х
у
СВОЙСТВА ФУНКЦИИ
Слайд 9ОПРЕДЕЛЕНИЕ
Число m называется наименьшим значением функции у = f(x) на
множестве X Є D(f), если:
Существует число x0 Є D(f) такое,
что f(x0) = M;Для любого значения х Є Х выполняется неравенство f(x) ≥ f(x0).
Слайд 10ОПРЕДЕЛЕНИЕ
Число m называется наибольшим значением функции у = f(x)
на множестве X Є D(f), если:
Существует число x0 Є D(f)
такое, что f(x0) = M;Для любого значения х Є Х выполняется неравенство f(x) ≤ f(x0).
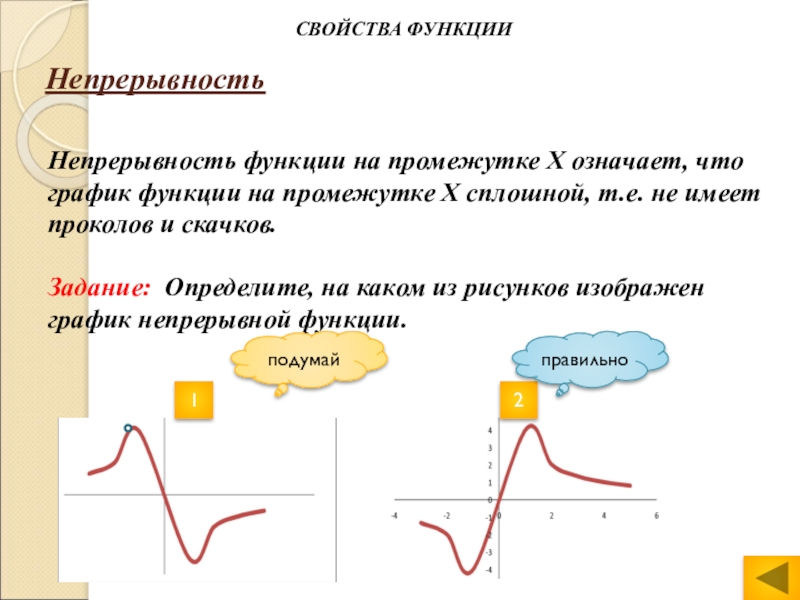
Слайд 11Непрерывность
Непрерывность функции на промежутке Х означает, что график функции на
промежутке Х сплошной, т.е. не имеет проколов и скачков.
Задание: Определите,
на каком из рисунков изображен график непрерывной функции.СВОЙСТВА ФУНКЦИИ
1
2
подумай
правильно
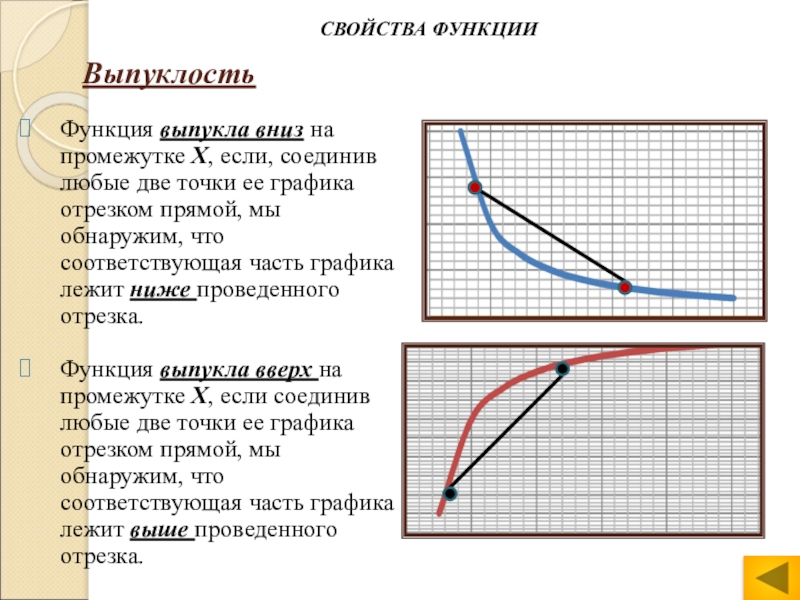
Слайд 12 Выпуклость
Функция выпукла вниз на промежутке Х,
если, соединив любые две точки ее графика отрезком прямой, мы
обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.Функция выпукла вверх на промежутке Х, если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
СВОЙСТВА ФУНКЦИИ
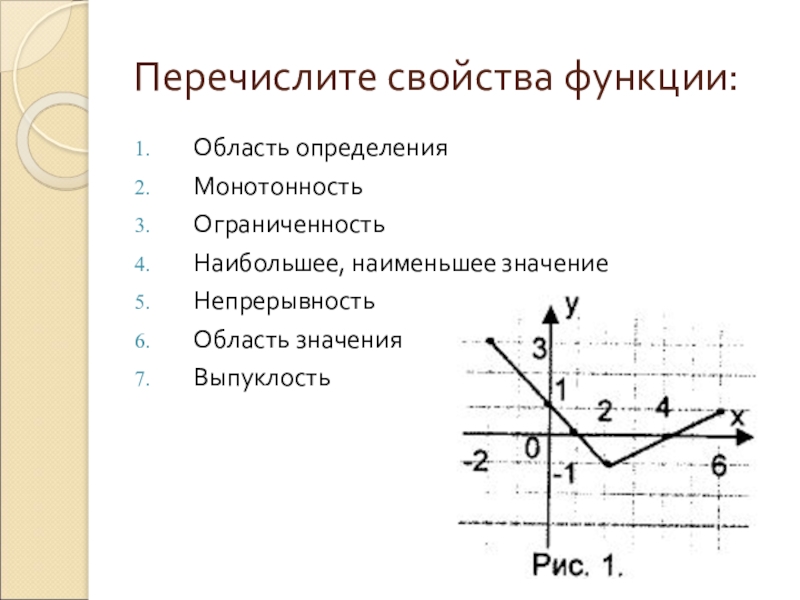
Слайд 13Перечислите свойства функции:
Область определения
Монотонность
Ограниченность
Наибольшее, наименьшее значение
Непрерывность
Область значения
Выпуклость
Слайд 141. Д (f) : [- 2; 6 ]
2. f(x)
убывает на [- 2; 2 ],
возрастает
на [ 2; 6 ],3. ограничена снизу
4. у наимен. = - 1 при х = 2,
у наиб. = 3 при х = - 2
5. f(x) непрерывна
6. Е (f) : [- 1; 3 ]
7. f(x) выпукла вниз
ПРОВЕРЬ СЕБЯ
![1. Д (f) : [- 2; 6 ]2. f(x) убывает на [- 2; 2 ],](/img/thumbs/1e41e1563bcead1fdc0dd72439ae353c-800x.jpg "Свойства функций. 1. Д (f) : [- 2; 6 ]2. f(x) убывает на")
Слайд 15Тестирование
1. На одном из рисунков изображен график функции, возрастающей
на промежутке [- 1;4]. Укажите этот рисунок.
![Тестирование 1. На одном из рисунков изображен график функции, возрастающей на промежутке [- 1;4]. Укажите этот рисунок.](/img/thumbs/bac685528f07d8457bb8d74143427caa-800x.jpg "Свойства функций. Тестирование 1. На одном из рисунков изображен график функции, возрастающей на")
Слайд 16Тестирование 2 На одном из рисунков изображен график функции, убывающей на
промежутке [0 ; 3 ].
Укажите этот рисунок.
![Тестирование 2 На одном из рисунков изображен график функции, убывающей на промежутке [0 ; 3 ].](/img/thumbs/821d782edb0816c8262a952f895929f7-800x.jpg "Свойства функций. Тестирование 2 На одном из рисунков изображен график функции, убывающей на")
Слайд 17Тестирование 3. На рисунке изображен график функции у = f(x).
Из приведенных утверждений выберите верное.
1. f(-1) < f(2)
2. функция у
= f(x) убывает на промежутке (-∞: 3]
3. f(0) = 2
4. функция принимает наименьшее значение при х =1.
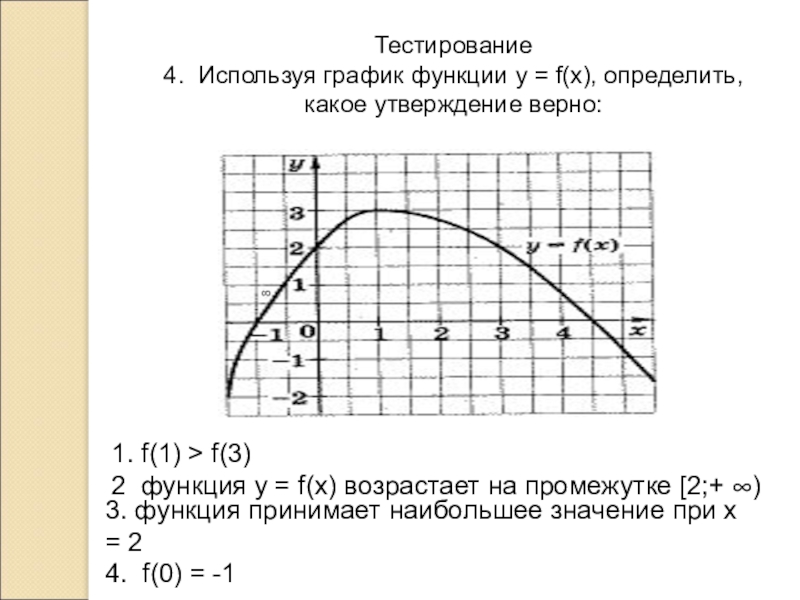
Слайд 18Тестирование 4. Используя график функции у = f(x), определить, какое утверждение
верно:
1. f(1) > f(3)
2 функция у = f(x) возрастает на
промежутке [2;+ ∞)
3. функция принимает наибольшее значение при х = 2
4. f(0) = -1
Слайд 19Тестирование 5. Используя график функции у = f(x), определить, какое утверждение
верно:
1. f(1) > f(0)
2 функция у = f(x) возрастает на
промежутке [2;+∞)
3. функция принимает наибольшее значение при х = 2
4. f(0) = -1
Слайд 21№ 10.14
Область определения
Монотонность
Ограниченность
Наибольшее, наименьшее значение
Непрерывность
Область значения
Выпуклость
Слайд 22ПРОВЕРЬ СЕБЯ
1.. Д (f) : (- ∞; + ∞
)
2.f(x) убывает на (-∞ ; 0 ], возрастает на
[ 0; + ∞ )3.ограничена сверху при х ≤ 0 и снизу при х ≥ 0
4.у наимен. , у наиб. не существует
5.f(x) имеет точку разрыва х = 0
6.Е (f) : (- ∞; + ∞ )
7.f(x) выпукла вверх
