Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические страницы истории Древней Индии 5 класс
Содержание
- 1. Математические страницы истории Древней Индии 5 класс
- 2. Из четырёх жертвователей второй дал вдвое больше
- 3. Семьдесят полос из березовой коры, неизвестной даты
- 4. СТРАНИЦЫИСТОРИИ индииМАТЕМАТИЧЕСКИЕ ДРЕВНЕй
- 5. Слайд 5
- 6. Система счисления кхарошти имела хождение в Индии
- 7. Наряду с этой системой существовала в
- 8. В древней Индии так же была словесная
- 9. Современная десятичная позиционная система возникла на основе
- 10. Слайд 10
- 11. В Бахшалийской рукописи для обозначения нуля применяется
- 12. Индийские математики не занимались доказательствами, но они
- 13. Дроби в Индии записывались вертикально, как делаем
- 14. Решите уравнения.
- 15. Самостоятельная работа. Вычислите.ВАРИАНТ 1.ВАРИАНТ 2.
- 16. ФИЗМИНУТКА
- 17. Древнеиндийские астрономы делили солнечный год на 12
- 18. Месяцы:Чайтра — (март-апрель)Вайшакха — (апрель-май)Джьяйштха — (май-июнь)Ашадха — (июнь-июль)Шравана — (июль-август)Бхадрапада — (август-сентябрь)Ашвина — (сентябрь-октябрь)Карттика — (октябрь-ноябрь)Маргаширша — (ноябрь-декабрь)Пауша — (декабрь-январь)Магха — (январь-февраль)Пхальгуна — (февраль-март)
- 19. Древние индийцы знали, что длина дня изменяется
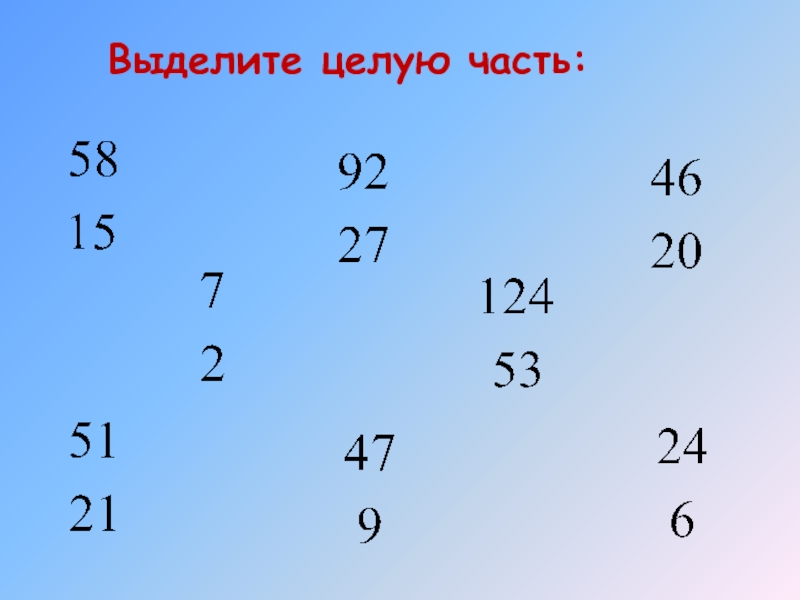
- 20. Выделите целую часть:
- 21. Запишите в виде неправильной дроби:
- 22. № 1134.
- 23. ДЛЯ МЕНЯ БЫЛО ОТКРЫТИЕМ, ЧТО… ДОСТОЯНИЕМ ПОТОМКОВ СТАЛО…
- 24. Домашнее задание. Узнать, какие системы счисления называются позиционными и непозиционными . № 1140
- 25. Спасибо за урок. До новых встреч.
- 26. Слайд 26
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Историческое деяние бывает закончено не только, когда оно свершилось, а
лишь после того, как оно становится достоянием потомков.
Слайд 2Из четырёх жертвователей второй дал вдвое больше первого, третий -
втрое больше второго, четвёртый - вчетверо больше третьего, а все
вместе дали 132. Сколько дал первый?Решение:
Автор рукописи решил задачу в частном виде, когда искомое предлагается равным единице. Пусть неизвестное равняется единице , тогда первый дал 1 , второй –2, третий –6, четвертый – 24. Сумма пожертвований будет равна 33. Разделим 132: 33= 4.
Ответ: первый дал 4.
Задача из Бахшалийской рукописи
Слайд 3Семьдесят полос из березовой коры, неизвестной даты и неизвестного происхождения,
– ее относят и к третьему, и к двенадцатому столетию.
Она содержит традиционный индийский материал о неопределенных и
о квадратных
уравнениях, а также
о приближениях,
и в ней для обозначения
нуля применяется точка.
Слайд 6Система счисления кхарошти имела хождение в Индии между VI веком
до нашей эры и III веком нашей эры. Эта была
непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.Древнеиндийские
системы счисления
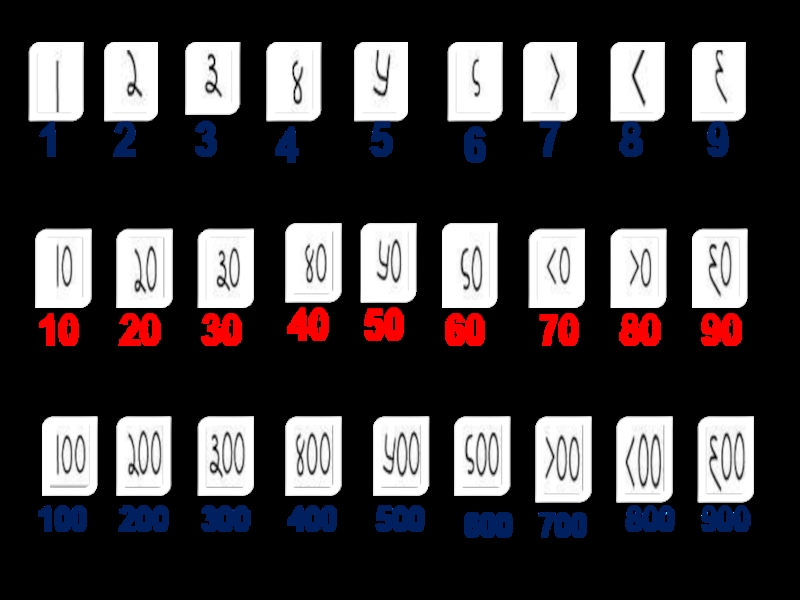
Слайд 7 Наряду с этой системой существовала в Индии еще одна
система счисления брахми. Числа брахми записывались
слева направо.
Однако в
обеих системах было
не мало общего.
В частности
первые три цифры
очень похожи.
Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы
Слайд 8В древней Индии так же была словесная система счисления. Знак
нуля произносился как «пустое», или «небо», или «дыра».
Единица как
«луна», или «земля».Двойка как «близнецы», или «глаза», или «ноздри», или «губы».
Четыре как «океаны», «стороны света».
Например, число 2441 произносилось так:
глаза океанов стороны света луны.
Слайд 9Современная десятичная позиционная система возникла на основе нумерации, зародившейся не
позднее 5 в. в Индии.
Наша современная система счисления, основанная
на позиционном принципе записи чисел и нуля как кардинального числа и использовании обозначения пустого разряда, называется индо-арабской. На стене храма, построенного в Индии ок. 250 до н.э., обнаружено несколько цифр, напоминающих по своим очертаниям наши современные цифры.
Слайд 11В Бахшалийской рукописи для обозначения нуля применяется точка.
Самый древний письменный документ со значком для нуля
относится к девятому столетию.Все это значительно более позднего происхождения, чем знак для нуля в вавилонских текстах. Быть может, знак 0 для нуля возник под греческим влиянием («ouden» – греческое слово, означающее ничто); в то время как вавилонскую точку писали только между цифрами, индийский нуль появляется также на последнем месте, и таким образом 0, 1, 2, ..., 9 становятся равноправными цифрами.
Слайд 12Индийские математики не занимались доказательствами, но они ввели оригинальные понятия
и ряд эффективных методов.
Махавира (850 н.э.) установил правила операций
с нулем, полагая, однако, что деление числа на нуль оставляет число неизменным. Правильный ответ для случая деления числа на нуль был дан Бхаскарой (р. в 1114), ему же принадлежат правила действий над иррациональными числами.
Индийцы ввели понятие отрицательных чисел (для обозначения долгов). Самое раннее их использование мы находим у Брахмагупты (ок. 630).
А вот геометрия по каким-то причинам вызывала у индийцев слабый интерес. Доказательства теорем состояли из чертежа и слова «смотри». Формулы для площадей и объёмов, они, скорее всего, унаследовали от греков.
Слайд 13Дроби в Индии записывались вертикально, как делаем и мы, только
вместо черты дроби их заключали в рамку (так же, как
в Китае и у поздних греков). Действия с дробями ничем не отличались от современных.Слайд 17Древнеиндийские астрономы делили солнечный год на 12 месяцев по 30
дней в каждом, причём через каждые пять лет добавлялся тринадцатый
месяц.
Древнеиндийские астрономы
знали о шаровидности
Земли и предполагали её
вращение вокруг своей оси.
Древнеиндийский календарь
Слайд 18
Месяцы:
Чайтра — (март-апрель)
Вайшакха — (апрель-май)
Джьяйштха — (май-июнь)
Ашадха — (июнь-июль)
Шравана — (июль-август)
Бхадрапада — (август-сентябрь)
Ашвина — (сентябрь-октябрь)
Карттика — (октябрь-ноябрь)
Маргаширша — (ноябрь-декабрь)
Пауша —
(декабрь-январь)
Магха — (январь-февраль)
Пхальгуна — (февраль-март)
Слайд 19Древние индийцы знали, что длина дня изменяется в зависимости от
времени года; детальное и точное измерение и правила вычисления длины
дня для любого времени года приведены в «Веданге-джйотиша».Веданга Джйотиша - это небольшая книга, написанная мудрецом Лагадхой, которая содержит все фундаментальные вычисления сезонов и разных начал года, используемых для различных целей.






































![Сложение и вычитание вида []+4, []-4](/img/thumbs/605739bbda80b8f279b676f7db1e2062-800x.jpg)

