Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сызы?ты? функция графиктеріні? ?зара орналасуы
Содержание
- 1. Сызы?ты? функция графиктеріні? ?зара орналасуы
- 2. Пысықтау сұрақтары:Қандай функция сызықтық деп аталады?Сызықтық функцияның
- 3. ҚАТЕНІ ТАП!Оқушы функциялардың бірінің графигін салғанда қате
- 4. Сызықтық функциялардың графиктерін зерттеу.Функцияның графигін тұрғызу үшін
- 5. Сызықтық функциялардың графиктерін зерттеу.Функцияның графигін тұрғызу үшін
- 6. Графиктерді бір координаталық жүйеде салып, сұрақтарға жауап
- 7. Тексеріп көрелік!УХу=2х+4у=2ху=2х-2у=2х-4УХу=-2х+4у=-2ху=-2х-2у=-2х-4қорытынды: егер бұрыштық коэффициенттер тең болса, түзулер параллель болады.
- 8. Дұрыс жауапты табыңдар:УХ311-2-25-23221-14у=-2ху=0,5х+3у=1у=2ху=-2
- 9. Зерттеуге тағы да сауал!Алдыңғы суреттен өзара перпендикуляр екі түзуді табыңдар!
- 10. Дұрыс! Бұл у= 0,5х+3 және у= - 2х түзулеріАл міне тағы бірнеше мысалдар
- 11. УХ1531у=0,2х+1у= - 5х+3УХ3-1-345у=-1/3 х+3У=3x-1
- 12. АЛ ЕНДІ ПЕРПЕНДИКУЛЯР ТҮЗУЛЕРДІҢ ТЕҢДЕУЛЕРІНЕ МҰҚИЯТ ҚАРАП,
- 13. Көңілімізді түсірмейміз!Міне бірінші көмек:Бұрыштық коэффициентке көңіл бөліңіз:
- 14. Сонымен, екі түзу қай кезде перпендикуляр?Қорытынды :
- 15. Ендеше барлық зерттеулеріміздің нәтижелерін қорытындылап, нақтылайық …
- 16. k саны:
- 17. l саны:ух0у= к ху= кх +l2l2y=1kx + l1l1
- 18. Өздік жұмыс тапсырмалары !y=k1x+l1 және
- 19. ОҚУЛЫҚПЕН ЖҰМЫС№1388,№1391,№1396
- 20. Сабақтағы жұмыстарыңызға рахмет!
- 21. Скачать презентанцию
Пысықтау сұрақтары:Қандай функция сызықтық деп аталады?Сызықтық функцияның графигі қандай болады?Тура пропорционалдық қандай формуламен беріледі?Қандай жағдайда сызықтық функция графиктері өспелі(кемімелі) болады?у=L функциясы қалай аталады?y=kx+l түріндегі түріндегі функцияны сызықтық функция деп атайдыСызықтық функцияның
Слайды и текст этой презентации
Слайд 1Сызықтық функциялар графиктерінің өзара орналасуы.
Зерттеу сабағы
Математика , 6 сынып
Круглоозерный ОЖББ
мектебі
Слайд 2Пысықтау сұрақтары:
Қандай функция сызықтық деп аталады?
Сызықтық функцияның графигі қандай болады?
Тура
пропорционалдық қандай формуламен беріледі?
Қандай жағдайда сызықтық функция графиктері өспелі(кемімелі) болады?
у=L
функциясы қалай аталады?y=kx+l түріндегі түріндегі функцияны сызықтық функция деп атайды
Сызықтық функцияның графигі түзу сызық болады
y=kx түріндегі функция тура пропорционалдық
Егер k>0, онда өспелі; егер k<0,онда кемімелі.
у=L – тұрақты функция деп аталады, графигі Ох осіне параллель түзу.
Слайд 3ҚАТЕНІ ТАП!
Оқушы функциялардың бірінің графигін салғанда қате жіберді. Қай суретте
қате бар?
Х
у=2х+3
У
Х
у=0,5х
3
-2
2
-3
У
Х
-2
-2
у= - х - 2
У
1
2
3
Слайд 4Сызықтық функциялардың графиктерін зерттеу.
Функцияның графигін тұрғызу үшін кестелерді толтырыңдар
1 вариант
2
вариант
1) у=2х+4
у
х
2) у=2х
х
у
3) у=2х-2
х
у
4) у=2х-4
х
у
1) у= - 2х+4
х
у
2) у= -
2хх
у
3) у= - 2х - 2
х
у
4) у= - 2х - 4
х
у
0
- 2
0
2
0
2
0
2
0
2
0
- 2
0
2
0
- 2
Слайд 5Сызықтық функциялардың графиктерін зерттеу.
Функцияның графигін тұрғызу үшін кестелерді толтырыңдар
1 вариант
2
вариант
1) у=2х+4
у
х
2) у=2х
х
у
3) у=2х-2
х
у
4) у=2х-4
х
у
1) у= - 2х+4
х
у
2) у= -
2хх
у
3) у= - 2х - 2
х
у
4) у= - 2х - 4
х
у
0
- 2
0
2
0
2
0
2
0
2
0
- 2
0
2
0
- 2
4
0
4
0
0
4
0
- 4
- 2
2
- 2
2
- 4
0
- 4
0
Слайд 6Графиктерді бір координаталық жүйеде салып, сұрақтарға жауап бере отырып, қорытынды
шығарып көр:
Барлық түзулер қалай орналасқан?
Барлық формулаларда ортақ не бар?
Әр функцияның
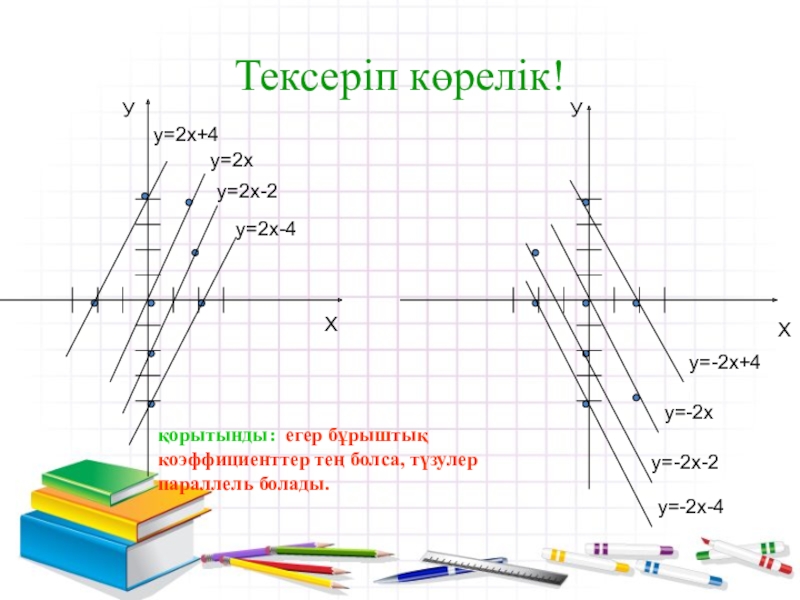
бұрыштық коэффициентінің мәні қандай?
Слайд 7Тексеріп көрелік!
У
Х
у=2х+4
у=2х
у=2х-2
у=2х-4
У
Х
у=-2х+4
у=-2х
у=-2х-2
у=-2х-4
қорытынды: егер бұрыштық коэффициенттер тең болса, түзулер параллель болады.
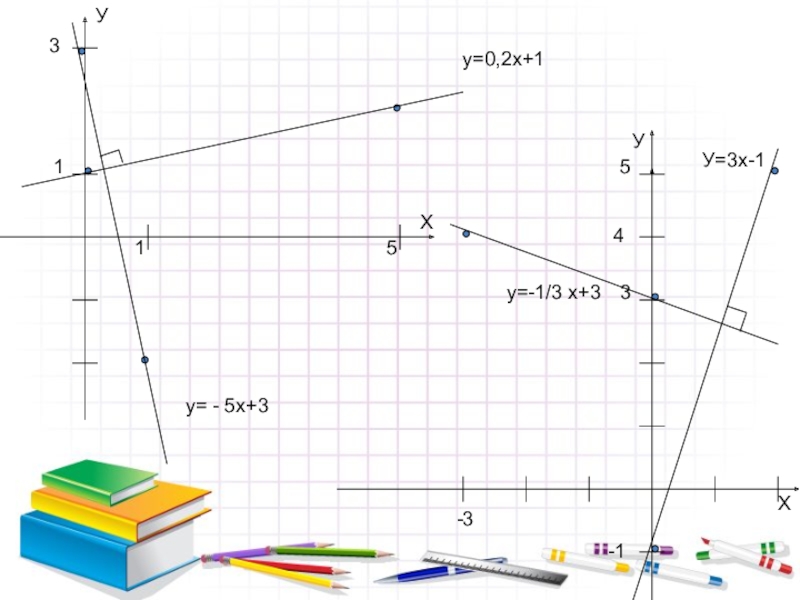
Слайд 12АЛ ЕНДІ ПЕРПЕНДИКУЛЯР ТҮЗУЛЕРДІҢ ТЕҢДЕУЛЕРІНЕ МҰҚИЯТ ҚАРАП, СҰРАҚТАРҒА ЖАУАП БЕРІП
КӨРІҢДЕР:
Қандай жағдайдар екі түзу өзара
перпендикуляр болады?
у= 0,5х+3
жәнеу= - 2х
у= - 5х+3
және
у= 0,2х+1
у=3х – 1
және
у=- 1/3 х+3
Шынымен біле алмадыңдар ма?!
Слайд 13Көңілімізді түсірмейміз!
Міне бірінші көмек:
Бұрыштық коэффициентке көңіл бөліңіз:
0,5 және -
2 - 5 және 0,2
3 және – 1/3Екінші көмек:
Бұрыштық коэффициенттерді көбейтіңіз:
0,5 *(-2)= -1 - 5*0,2= -1 3* (-1/3)= -1
Слайд 14Сонымен, екі түзу қай кезде перпендикуляр?
Қорытынды : екі түзу перпендикуляр
болады, егер олардың бұрыштық коэффициенттерінің көбейтіндісі
-1-ге тең болса
Слайд 15Ендеше барлық зерттеулеріміздің нәтижелерін қорытындылап, нақтылайық …
k бұрыштық коэффициенті
неге «жауап береді»?
Түзудің орналасуына l саны қалай «әсер етеді»?
Слайд 18Өздік жұмыс тапсырмалары !
y=k1x+l1 және y=k2x+l2 екі
сызықтық функциялары берілген. Мына шарттар орындалатындай k1, k2 , l1
, l2 сандарын таңдап алыңдар:- параллель болатын;
- қиылысатын;
- тік бұрыш жасап қиылысатын;
- беттесетін.
Сәйкес формулаларын жазыңдар.
