Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Безу
Содержание
- 1. Теорема Безу
- 2. Тема урока:«Теорема Безу»
- 3. Слайд 3
- 4. Как разложить на множители многочлен х2 -
- 5. Схема Горнера . x3-2x2-6x+4 разделим на
- 6. Значения
- 7. Теорема Безу:Остаток R от деления Р(х) на
- 8. РЕШИТЬ УРАВНЕНИЕ:х4 - x3 - 6x2 - x + 3 = 0.Ответ: -1; 3;
- 9. ЗАКЛЮЧЕНИЕ Теорема Безу дает возможность, найдя
- 10. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3
Решить уравнение:
x3-2x2-6x+4=0Проблема:
Возможно ли многочлен третьей степени x3-2x2-6x+4
разложить на множители?
Слайд 4
Как разложить на множители многочлен х2 - 5х - 6?
х2
- 5х - 6 = (х – 6)(х + 1)
Вывод:
Корни трехчлена являются делителями свободного члена.
.
Слайд 5
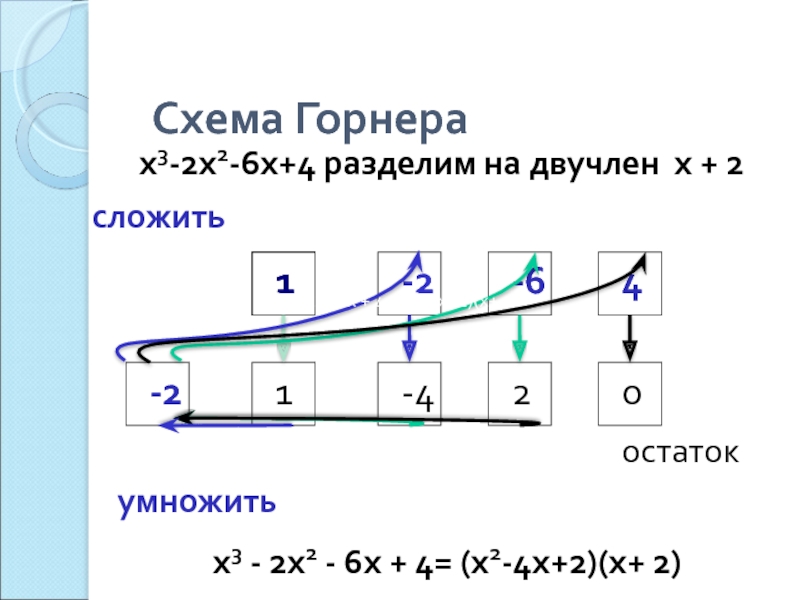
Схема Горнера
.
x3-2x2-6x+4 разделим на двучлен х + 2
1
-2
-6
4
1
1
-4
2
0
-2
остаток
умножить
сложить
x3 - 2x2 - 6x + 4= (x2-4x+2)(x+ 2)
x3
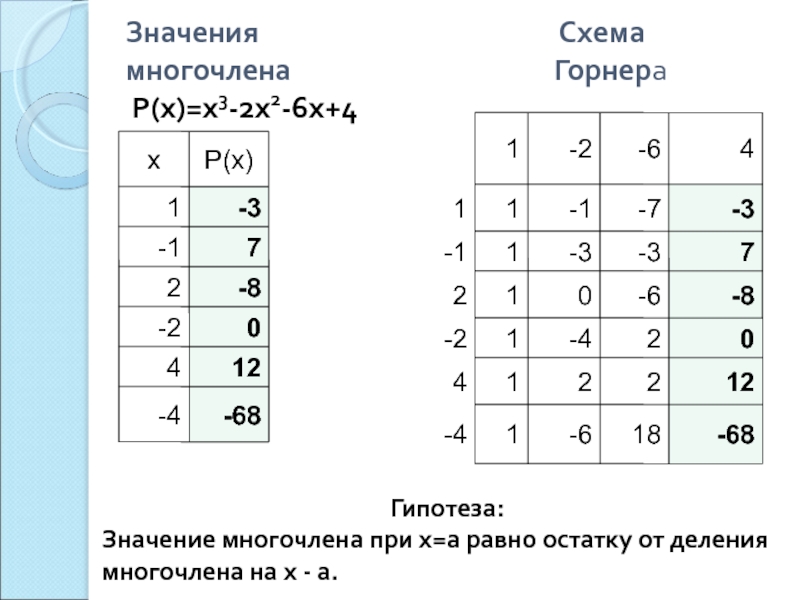
- 2x2 - 6x + 4= (x2-4x+2)(x+ 2)=Слайд 6Значения
Схема многочлена Горнера Р(х)=x3-2x2-6x+4
Гипотеза:
Значение многочлена при х=а равно остатку от деления многочлена на х - а.
Слайд 7Теорема Безу:
Остаток R от деления Р(х) на двучлен (x -
а) равен Р(а).
Следствие: Для того, чтобы многочлен Р(х) делился нацело
на двучлен (х – а), необходимо и достаточно, чтобы выполнялось равенство Р(а) = 0.О Безу
Этьенн БЕЗУ
Этьенн Безу (1730 - 1783)
Слайд 9
ЗАКЛЮЧЕНИЕ
Теорема Безу дает возможность, найдя один корень многочлена, искать далее
корни многочлена, степень которого на 1 меньше: если Р(а) =
0, то Р(х)= (x - а)∙Q(x), и остается решить уравнение Q(x) = 0.Иногда этим приемом - он называется понижением степени - можно найти все корни многочлена.
В начало