Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Пифагора. Различные способы ее доказательства
Содержание
- 1. Теорема Пифагора. Различные способы ее доказательства
- 2. Биография Пифагора.Пифагор Самосский (др.-греч. (др.-греч. Πυθαγόρας ὁ Σάμιος; 570 (др.-греч. Πυθαγόρας ὁ Σάμιος; 570—490 (др.-греч. Πυθαγόρας
- 3. Биография Пифагора. Родители – Мнесарх и Партенида
- 4. Пифогорейская школа. Условия приёма в школу
- 5. Легенды и мифыУмел разговаривать с птицами и
- 6. Изречения ПифагораВеликая наука жить счастливо состоит в
- 7. Музыка и ПифагорПифагор и его последователи рассчитали
- 8. История возникновения теоремы Пифагора.Теорема Пифагора — одна из
- 9. История возникновения теоремы Пифагора.В древнекитайской книге Чжоу би
- 10. История возникновения теоремы Пифагора.Мориц КанторМориц Кантор (крупнейший немецкий
- 11. История возникновения теоремы Пифагора.Несколько больше известно о
- 12. История возникновения теоремы Пифагора.Согласно комментарию ПроклаСогласно комментарию Прокла к ЕвклидуСогласно комментарию Прокла к Евклиду, ПифагорСогласно
- 13. История возникновения теоремы Пифагора.По преданию, ПифагорПо преданию, Пифагор отпраздновал открытие
- 14. Формулировка теоремы« Доказать, что квадрат, построенный
- 15. Формулировка теоремы«У Евклида эта теорема гласит
- 16. Формулировка теоремыВ Geometria Culmonensis (около 1400
- 17. Формулировка теоремы«У Евклида эта теорема гласит
- 18. Современная формулировка« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 19. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
- 20. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. ca
- 21. В одном случае (слева) квадрат
- 22. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
- 23. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного
- 24. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 25. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 26. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим
- 27. V. Доказательство теоремы через подобные треугольники.Пусть ABC есть прямоугольный
- 28. V. Доказательство теоремы через подобные треугольники. Введя обозначения получаем что эквивалентно
- 29. V. Доказательство теоремы через подобные треугольники. сложив получаем или
- 30. Значение теоремы ПифагораТеорема Пифагора- это одна
- 31. Доказательство теоремы Пифагора учащиеся средних веков считали
- 32. СПАСИБО ЗА ВНИМАНИЕ!
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Биография Пифагора.
Пифагор Самосский (др.-греч. (др.-греч. Πυθαγόρας ὁ Σάμιος; 570 (др.-греч. Πυθαγόρας ὁ Σάμιος; 570—490 (др.-греч. Πυθαγόρας ὁ Σάμιος; 570—490 гг. до н. э.) —
древнегреческий философ (др.-греч. Πυθαγόρας ὁ Σάμιος; 570—490 гг. до н. э.) — древнегреческий философ,математик (др.-греч. Πυθαγόρας ὁ Σάμιος; 570—490 гг. до н. э.) — древнегреческий философ,математик и мистик, создатель религиозно-философской школы пифагорейцев.
Слайд 3Биография Пифагора.
Родители – Мнесарх и Партенида с Самоса
В 18-летнем
возрасте отправился в путешествие в Египет, Вавилон
Вернулся на родину в
56 летВ греческой колонии Кротоне в Южной Италии основал свою школу
Был женат на своей ученице Феано, имел сына и дочь.
Слайд 4Пифогорейская школа.
Условия приёма в школу Пифагора:
отказаться от личной
собственности в пользу союза
не проливать крови
не употреблять мясной пищи
беречь тайну
учения своего учителяне обучать других за вознаграждение
Слайд 5Легенды и мифы
Умел разговаривать с птицами и животными
Повелевал духами и
делал предсказания
Способен раздваиваться
Исцелял людей
Перевоплощённый бог Аполлон
Имел золотое бедро
Слайд 6Изречения Пифагора
Великая наука жить счастливо состоит в том, чтобы жить
только в настоящем.
Дружба есть равенство.
Жизнь подобна игрищам:
иные приходят на них состязаться, иные торговать, а самые счастливые — смотреть. Из двух человек одинаковой силы сильнее тот, кто прав.
Слайд 7Музыка и Пифагор
Пифагор и его последователи рассчитали т.н. пифагоров строй
-математическое выражение интервалов между звуками гаммы (т.н. «лидийской» гаммы).
4
Слайд 8История возникновения теоремы Пифагора.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии —
одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонамипрямоугольного треугольника.
Слайд 9История возникновения теоремы Пифагора.
В древнекитайской книге Чжоу би суань цзин говорится о
пифагоровом треугольнике со сторонами 3, 4 и 5. В этой
же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.Слайд 10История возникновения теоремы Пифагора.
Мориц КанторМориц Кантор (крупнейший немецкий историк математики) считает,
что равенство 3 ² + 4 ² = 5² было
известно уже египтянам ещё около 2300 г. до н. э.Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.Слайд 11История возникновения теоремы Пифагора.
Несколько больше известно о теореме Пифагора у вавилонянНесколько
больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом
ко времени ХаммурапиНесколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника[2]. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях.Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников,Ван-дер-ВарденОсновываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников,Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теоремаОсновываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников,Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна в Вавилоне уже около XVIII века до н. э.
Слайд 12История возникновения теоремы Пифагора.
Согласно комментарию ПроклаСогласно комментарию Прокла к ЕвклидуСогласно комментарию Прокла к Евклиду, ПифагорСогласно комментарию Прокла к Евклиду, Пифагор использовал алгебраические методы,
чтобы находитьпифагоровы тройки. Однако Прокл писал, что не существует явного
упоминания, относящегося к периоду продолжительностью 5 веков после смерти Пифагора, что Пифагор был автором теоремы.Однако, когда авторы, такие как ПлутархОднако, когда авторы, такие как Плутарх иЦицерон, пишут о теореме Пифагора, они пишут так, как будто авторство Пифагора было широко известным и несомненным.«Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики».
Слайд 13История возникновения теоремы Пифагора.
По преданию, ПифагорПо преданию, Пифагор отпраздновал открытие своей теоремы гигантским
пиром, заклав на радостях сотню быков.Приблизительно в 400 г. до н. э., согласно
Проклу, ПлатонПо преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков.Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» ЕвклидаПо преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков.Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.Слайд 14Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника,
равновелик сумме квадратов, построенных на катетах»
« Площадь квадрата, построенного
на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Во времена Пифагора теорема звучала так:
или
Слайд 15Формулировка
теоремы
«У Евклида эта теорема гласит (дословный перевод): "В прямоугольном
треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на
сторонах, заключающих прямой угол".»Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ) в переводе на русский гласит:"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
Слайд 16Формулировка
теоремы
В Geometria Culmonensis (около 1400 г.) в переводе теорема
читается так : "Итак, площадь квадрата, измеренного по длинной стороне,
столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Слайд 17Формулировка
теоремы
«У Евклида эта теорема гласит (дословный перевод): "В прямоугольном
треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на
сторонах, заключающих прямой угол".»Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ) в переводе на русский гласит:"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
Слайд 18Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов».
Слайд 19Доказательства теоремы
Существует около 500 различных доказательств этой теоремы
(геометрических, алгебраических, механических и т.д.).
Слайд 20Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a
+ c.
c
a
Слайд 21
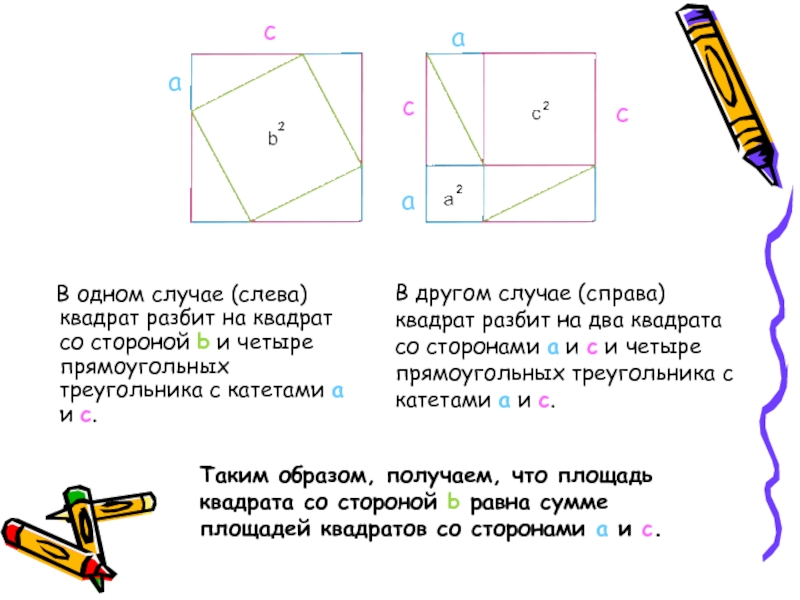
В одном случае (слева) квадрат разбит на квадрат
со стороной b и четыре прямоугольных треугольника с катетами a
и c.a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
Слайд 23Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а
ACFG и BCHI-квадраты, построенные на его катетах. Опустим из вершины
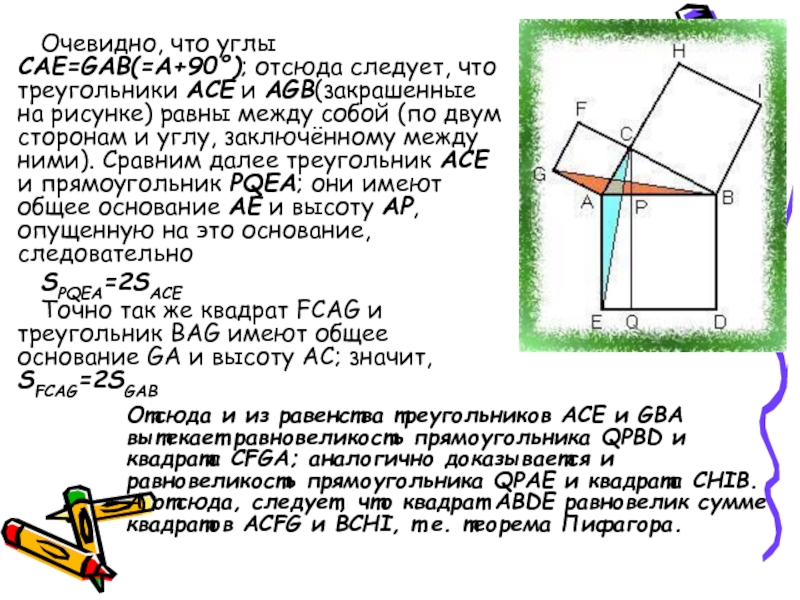
C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G.Слайд 24Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и
AGB(закрашенные на рисунке) равны между собой (по двум сторонам и
углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательноSPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
Слайд 25Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого
угла С.
2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB,
значит AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Слайд 26Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку
AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим
перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.