Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Фалеса
Содержание
- 1. Теорема Фалеса
- 2. Цель и задача урокаЦель
- 3. Слайд 3
- 4. Фалес считается родоначальником античной и,
- 5. Теорема Фалеса Если параллельные прямые, пересекающие
- 6. Доказательство: Пусть А3ОВ3 – заданный угол,
- 7. Теорема
- 8. Доказательство: Пусть на прямой l 1
- 9. Применение теоремы Фалеса
- 10. Доказательство: Пусть отрезок DE – средняя
- 11. Задача 1 Дан треугольник
- 12. Решение: Проведем прямые параллельные
- 13. Слайд 13
- 14. Решение: Проведем луч AX, не лежащий на
- 15. Слайд 15
- 16. Решение: Проведем какой-нибудь луч АМ, не
- 17. Заключение: В представленной работе рассмотрена теорема
- 18. Скачать презентанцию
Цель и задача урокаЦель данного урока знакомство с жизнедеятельностью философа и мыслителя Фалеса и его теоремой; развитие «геометрического зрения», расширение кругозора в плане знакомства с историей развития математики.Задачи:
Слайды и текст этой презентации
Слайд 2 Цель и задача урока
Цель данного урока знакомство
с жизнедеятельностью философа и мыслителя Фалеса и его теоремой; развитие
«геометрического зрения», расширение кругозора в плане знакомства с историей развития математики.Задачи:
- продемонстрировать возможности применения теоремы Фалеса в различных геометрических задачах
- расширить представления о сферах применения полученных математических знаний;
- познакомиться с историческими сведениями об ученом Фалесе, о развитии математических знаний и их применениях
Слайд 3 Фалес
Фалес из Милета - первый древнегреческий мыслитель. По-видимому, он
жил в 640-546 годах до н.э. Он первый применил доказательство теорем и ввел их в обиход математики. Основатель милетской школы. Считался первым из Семи мудрецов Греции.Слайд 4
Фалес считается родоначальником античной и, как следствие, европейской
философии и науки. Считался первым из Семи мудрецов Греции.
Важнейшей заслугой Фалеса в области математики должно быть перенесенное им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалесу открытие следующих геометрических предложений:▪ Вертикальные углы равны.
▪ Углы при основании равнобедренного треугольника равны.
▪ Треугольник определяется стороной и прилежащими к ней двумя углами.
▪ Диаметр делит круг на две равные части.
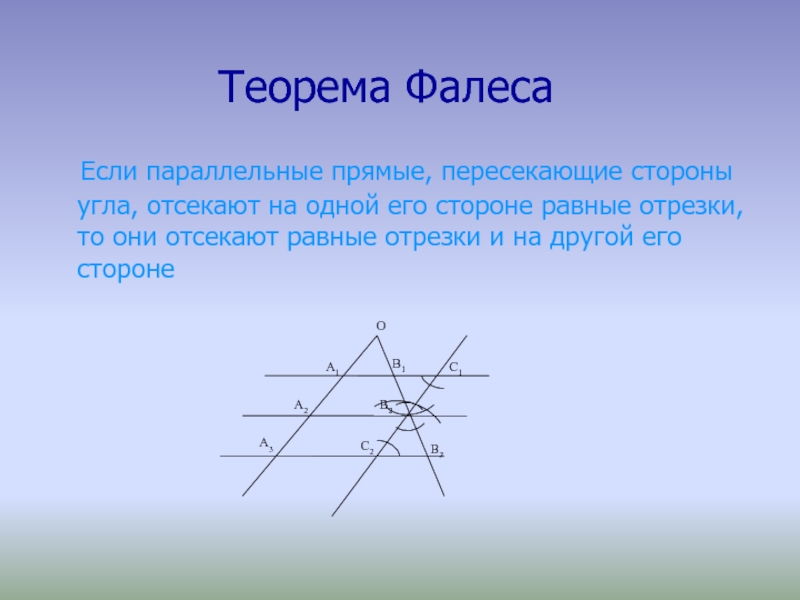
Слайд 5Теорема Фалеса
Если параллельные прямые, пересекающие стороны угла, отсекают
на одной его стороне равные отрезки, то они отсекают равные
отрезки и на другой его сторонеСлайд 6Доказательство:
Пусть А3ОВ3 – заданный угол, а А1В1, А2В2,
и А3В3– попарно параллельные прямые и А1А2=А2А3. Докажем, что В1В2=В2В3.
Проведем через точку В2 прямую С1С2 параллельную прямой А1А3. По лемме А1А2 =С1В2, А2А3 = В2С2 и с учетом условия теоремы С1В2 = В2С2. Кроме того, ∠В1С1В2 = ∠В2С2В33– как внутренние накрест лежащие при параллельных прямых А1В1, А3В3 и секущей С1С2 , а ∠В1В2С1 = ∠С2В2В3 как вертикальные. По второму признаку равенства треугольников ΔВ1С1В2 = ΔВ3С2В2. Отсюда В1В2 = В2В3. Теорема доказана.Слайд 7 Теорема Фалеса
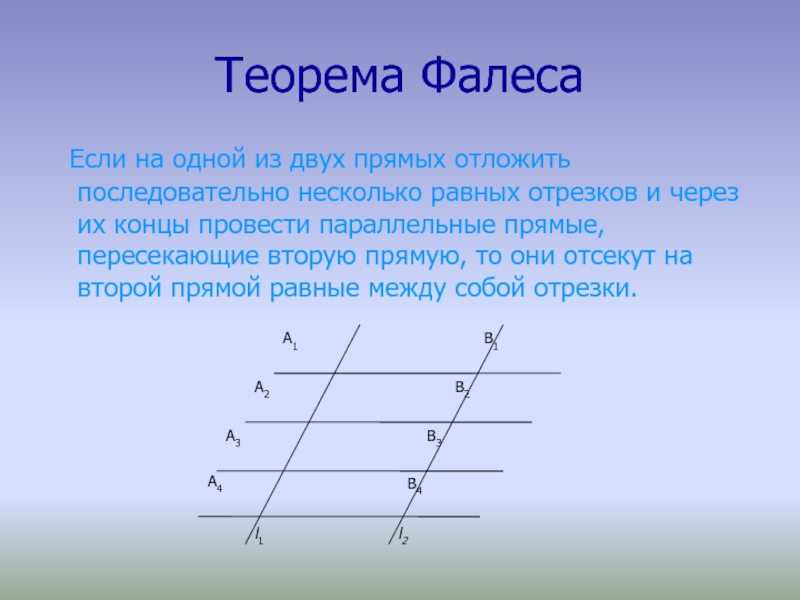
Если на
одной из двух прямых отложить последовательно несколько равных отрезков и
через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.Слайд 8Доказательство:
Пусть на прямой l 1 отложены равные отрезки
A1A2, A2A3, А3А4 и через их концы проведены параллельные прямые,
которые пересекают прямую l 2 в точках B1, B2, B3, В4 как рисунке 4. Требуется доказать, что отрезки B1B2, B2B3, В3В4 равны друг другу. Докажем, что B1B2=B2B3.Рассмотрим случай, когда прямые l 1 и l 2 параллельны. Тогда A1A2=B1B2 и A2A3=B2B3 как противоположные стороны параллелограммов A1B1B2A2 и A2B2B3A3. Так как A1A2= A2A3, то и B1B2=B2B3. Теорема доказана.
Слайд 9 Применение теоремы Фалеса
к решению задач
Средняя линия треугольника
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Слайд 10Доказательство:
Пусть отрезок DE – средняя линия в треугольнике
ABC, т.е. AE = EC, CD = BD. Проведем через точку D прямую a,
параллельную стороне AB. По теореме Фалеса прямая a пересекает сторону AC в ее середине и, следовательно, содержит среднюю линию DE. Значит, средняя линия DE параллельна стороне AB. Проведем среднюю линию DF. Она параллельна стороне AC. Тогда по лемме отрезок ED равен отрезку AF и равен половине отрезка AB. Теорема доказана.Слайд 11 Задача 1
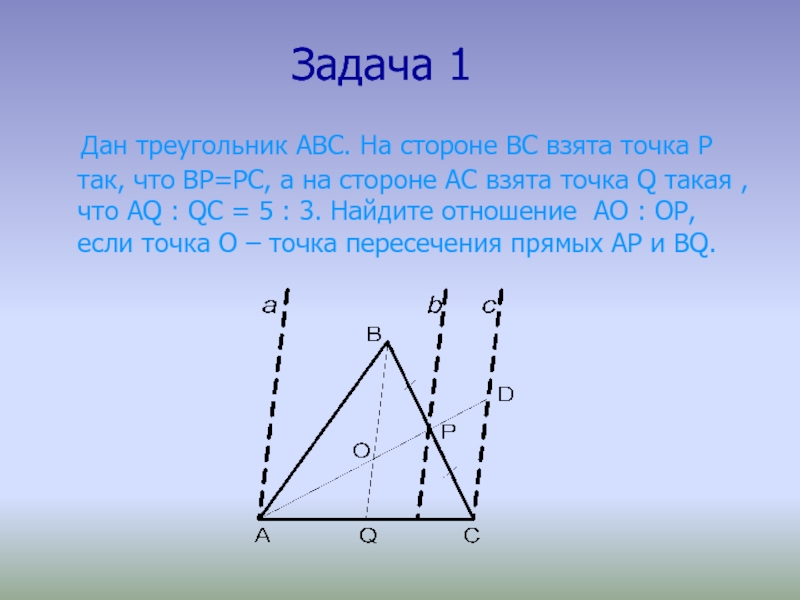
Дан треугольник АВС. На стороне
ВС взята точка Р так, что ВР=РС, а на стороне
АС взята точка Q такая , что АQ : QС = 5 : 3. Найдите отношение АО : ОР, если точка О – точка пересечения прямых АР и ВQ.
Слайд 12 Решение:
Проведем прямые параллельные ВQ через точки
А, Р и С. Точка D – это точка пересечения
прямых АР и с.По теореме Фалеса параллельные прямые ВQ, b и c, которые отсекают равные отрезки ВР и РС, отсекают равные отрезки ОР и РD на прямой АD.
По теореме Фалеса параллельные прямые a, BQ и с, которые отсекают на прямой АС отрезки в соотношении 5 : 3, отсекают и на прямой АD отрезки в соотношении 5 : 3.
То есть AQ : QC= 5:3 и AO : OD = 5:3, а отрезок OD=2OP. Следовательно, AO : OP = 10:3.
Ответ: 10 : 3.
Слайд 14Решение:
Проведем луч AX, не лежащий на прямой AB, и
на нем от точки A отложим последовательно n равных отрезков
АА1, А1А2, …,Аn-1An , т.е. на столько равных отрезков, на сколько равных частей нужно разделить данный отрезок AB. Проведем прямую AnB (точка Аn – конец последнего отрезка) и построим прямые, проходящие через точки A1, A2,…, An-1 и параллельные прямые прямой AnB. Эти прямые пересекают отрезок AB в точках B1, B2, …, Bn-1, которые по теореме Фалеса делят отрезок AB на n равных частей.Слайд 15 Задача 3
Разделите данный отрезок АВ на два отрезка АХ и ХВ,
пропорциональные данным отрезкам P1Q1 и P2Q2.
Слайд 16Решение:
Проведем какой-нибудь луч АМ, не лежащий на прямой
АВ, и на этом луче отложим последовательно отрезки АС и
CD, равные отрезкам P1Q1 и P2Q2. Затем проведем прямую BD и прямую, проходящую через точку С параллельно прямой BD. Она по теореме Фалеса пересечет отрезок АВв искомой точке Х.
Слайд 17Заключение:
В представленной работе рассмотрена теорема величайшего математика –
ученого – мыслителя Фалеса, задачи, в решении которых применяется различные
варианты этой теоремы.Решение геометрических задач различными способами является исследовательской частью данного урока и дает возможность сравнить разные способы решения и проанализировать их появление.
Теги